
|
|
Приближенные методы вычисления определенного интеграла.Выделим два направления приближенных вычислений интегралов: · направление, основанное на геометрической интерпретации определенного интеграла, то есть замене фигуры под кривой интегральной функции интегральной суммой элементарных трапеций; · направление, основанное на разложении подынтегральной функции в бесконечный степенной ряд. Приближенные методы интегрирования, основанные на геометрической интерпретации определенного интеграла.
квадратной параболой. В зависимости от этого методы называют формулами прямоугольников, трапеций или Симпсона.
прямоугольников: : Рис.2.11.
прямоугольников:
аппроксимируют наклонным отрезком прямой).
Формула трапеций дает результат средний арифметический от формул прямоугольников;
аппроксимируют дугой квадратной параболы). Квадратную параболу можно провести через три точки, поэтому отрезок интегрирования разбивают на четное число элементарных интервалов.
Таким образом, интеграл заменяют интегральной суммой, которая при достаточном числе членов даёт значение с любой степенью точности. Абсолютная погрешность вычисления интеграла определяется формулой: где ПРИМЕР 2.7. Вычислить по приближенным формулам с точностью РЕШЕНИЕ. Принимаем четное число дискретов
Вычисляем интеграл, используя результаты расчетов (таблица 2.1.). По формуле "левых" прямоугольников:
По формуле "правых" прямоугольников: По формуле трапеций:
По формуле Симпсона:
= Для сравнения точности приближенных вычислений по разным формулам вычисляем точное значение интеграла по формуле Ньютона-Лейбница:
Сведем все результаты в таблицу 2.2. Таблица 2.2.
Видим, что: - вычисление по формулам прямоугольников дает наибольшую ошибку; - вычисление по формуле трапеций даёт среднее арифметическое результатов, вычисленных по формулам прямоугольников. Погрешность при этом уменьшилась на два порядка; - вычисление по формуле Симпсона в требуемом разряде точности погрешности не дало. ПРИМЕР 2.8. Вычислить интеграл
РЕШЕНИЕ. Вычисляем ширину дискрета: Результаты вычислений сводим в таблицу 2.3. Таблица 2.3.
Оценим погрешность вычисления согласно (2.8.)
Таким образом,
2.7.2. Приближенное решение интегралов разложением подынтегральной функции в бесконечный степенной ряд. Метод основан на том, что сложная подынтегральная функция с помощью ряда Макларена заменяется на сумму степенных функций, которые легко интегрируются. Сложность заключается в том, что эта сумма является бесконечной. Числовой ряд является сходящимся. Поэтому конечное число слагаемых определяется требуемой точностью. Подробно этот метод рассматривается в разделе "Ряды".
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. Рассмотрим приложениеопределенного интеграла для решения геометрических и для решения экономических задач. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Если разбить отрезок интегрирования
Если разбить отрезок интегрирования  на
на  элементарных интервалов, то можно площадь криволинейной трапеции заменить суммой площадей элементарных трапеций. При этом
элементарных интервалов, то можно площадь криволинейной трапеции заменить суммой площадей элементарных трапеций. При этом 







 верхнюю сторону элементарной трапеции
верхнюю сторону элементарной трапеции можно аппроксимировать прямой или
можно аппроксимировать прямой или


 )формула левых (входящих, нижних)0
)формула левых (входящих, нижних)0 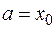

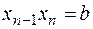
 (2.4.)
(2.4.) формула правых (выходящих, верхних)
формула правых (выходящих, верхних) (2.5.)
(2.5.) формула трапеций (верхнюю сторону элементарной трапеции
формула трапеций (верхнюю сторону элементарной трапеции (2.6.)
(2.6.) формула Симпсона (верхнюю сторону элементарной трапеции
формула Симпсона (верхнюю сторону элементарной трапеции (2.7.)
(2.7.) (2.8.)
(2.8.) - максимальное значение модуля второй производной подынтегральной функции на
- максимальное значение модуля второй производной подынтегральной функции на  интеграл
интеграл  и сравнить результаты с точным значением.
и сравнить результаты с точным значением.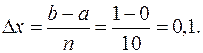
 .
.
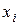








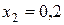
















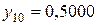










 по формуле трапеций при
по формуле трапеций при  и оценить погрешность.
и оценить погрешность.





 . Находим вторую производную подынтегральной функции.
. Находим вторую производную подынтегральной функции.  Полученная функция монотонно убывает, следовательно её максимальное значение на отрезке интегрирования находится в точке
Полученная функция монотонно убывает, следовательно её максимальное значение на отрезке интегрирования находится в точке 

 .
.