
|
|
Интегрирование по частям в неопределенном интеграле.12 Конспект лекций по
Интегральному исчислению
Интегральное исчисление Первообразная и неопределенный интеграл. Определение: Первообразной F(x) функции f(x) на промежутке называют функцию, производная которой Например: для функции Теорема Лемма. Если производная функции на промежутке Доказательство: По теореме Лагранжа для любых x1, x2 Î выполняется Теорема: Пусть функция F(x) –первообразная f(x), Ф(x) – другая первообразная f(x) Þ F(x)=Ф(x)+С. Доказательство: так как Таким образом, из теоремы следует, что выражение Определение: Неопределенным интегралом функции f(x) по переменной x называется множество всех её первообразных ò-знак интеграла, f(x) – подынтегральная функция, x – переменная интеграла, Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат. Свойства неопределенного интеграла.
Замечание: Условием существования неопределенного интеграла является непрерывность подынтегральной функции. Замена переменных в неопределенном интеграле. Пусть на промежутке T определена функция Первый тип.
Второй тип.
Пример: Таблица интегралов.
Интегрирование по частям в неопределенном интеграле. Т.к. Интегрирование по частям применяют в случаях: · Подынтегральная сумма представляет собой произведение многочлена на показательную функцию или тригонометрическую. За u берется многочлен, за dv оставшееся. Пример:
= · Подынтегральная функция представляет собой произведение многочлена на логарифмическую или обратную тригонометрическую функцию, за часть u нужно взять логарифмическую или обратную тригонометрическую функцию.
· Подынтегральная функция представляет собой произведение тригонометрической на показательную функцию. Неважно что брать за u.
1.6 Интегрирование выражений, содержащих квадратный трехчлен: а) выделяется полный квадрат в квадратном трехчлене
б) заменой Задача. Найти неопределенный интеграл
Решение: Выделим сначала полный квадрат из квадратного трехчлена:
Затем проведем замену переменных, положив Тогда Каждый из интегралов вычислим отдельно:
Здесь мы сделаем замену переменных, положив
Окончательно получим
= 1.7 Интегрирование рациональных дробей. Выражения вида
где Дроби вида Теорема. Любая правильная рациональная дробь может быть представлена в виде суммы простейших рациональных дробей (m и n-степени многочленов, стоящих в числителе и знаменателе соответственно). Эта сумма строится следующим образом в два этапа: 1) каждый простейший множитель вида 2) каждый сомножитель вида
В результате мы получим следующее разложение правильной дроби на простейшие:
Считая в дальнейшем, что коэффициент при старшей степени у многочлена Задача. Разложить дробь Решение: Разложим знаменатель на простейшие сомножители: Тогда
Две дроби, имеющие одинаковые знаменатели, равны, значит равны их числители, то есть Два многочлена тождественно равны тогда, когда у них совпадают коэффициенты при одинаковых степенях
Решая ее, находим, что Окончательно положим Задача. Разложить дробь Тогда
Как и в предыдущей задаче, составим систему уравнений для нахождения неизвестных коэффициентов:
Выражая из первых двух уравнений
Отсюда Следовательно,
Из разложения (5) следует, что интегрирование правильных рациональных дробей сводится к интегрированию простейших дробей.
Задача. Найти Решение: Поскольку рациональная дробь, стоящая под знаком интеграла, является неправильной, то представим ее в виде суммы многочлена и правильной дроби (для этого достаточно найти частное и остаток от деления числителя на знаменатель). Тогда Разложим дробь
Следовательно,
Но тогда
1.8 Интегрирование некоторых иррациональных алгебраических функций. Пусть Как правило, за Задача. Найти неопределенный интеграл Решение:Ясно, что
1.9 Интегрирование тригонометрических выражений.Пусть 1-й случай. Интеграл С учетом сделанной замены получим где Задача . Найти неопределенный интеграл: Решение: Сделаем универсальную тригонометрическую подстановку:
Тогда Последний интеграл вычислим отдельно. Для этого выделим полный квадрат в знаменателе дроби:
Воспользовавшись заменой переменной
Окончательно находим
Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам. 2-й случай. В интегралах
Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида
Задача. Найти неопределенный интеграл:
Решение: Сделаем подстановку:
Тогда
Задача. Найти неопределенный интеграл: Решение:
Интегрирование выражений вида
где mи n-целые числа. Рассмотрим два случая: 1-й случай. Среди чисел m,nесть хотя бы одно нечетное. Тогда за tпринимается функция, стоящая в основании другой степени. Задача. Найти неопределенный интеграл:
Решение: Здесь функция sinxстоит в нечетной степени, поэтому
2-й случай. В выражении (6) оба числаm,n- четные неотрицательные. Положим m=2p, n=2q и применим формулы:
Тогда Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. , первообразная
, первообразная  на R, так как
на R, так как  при любом х.
при любом х. , то
, то  .
. , где
, где 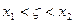 , так как
, так как  Þ
Þ  Þ
Þ 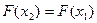 Þв силу произвольности точек x1 и x2 F(x) = C(const).
Þв силу произвольности точек x1 и x2 F(x) = C(const). Þ по Лемме
Þ по Лемме  Þ
Þ  .
. описывает все множество первообразных функции f(x).
описывает все множество первообразных функции f(x).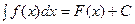 , где
, где  - подынтегральное выражение, С – const интегрированная.
- подынтегральное выражение, С – const интегрированная. ;
;  - верно
- верно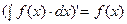



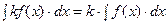


 , на множестве значений которой определена функция
, на множестве значений которой определена функция 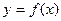 Þ
Þ  =
=  . Можно выделить два вида с заменой переменной.
. Можно выделить два вида с заменой переменной. Такие замены стандартные, их нужно знать.
Такие замены стандартные, их нужно знать. =
= 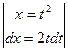 =
=  =
= 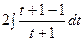 =
= 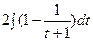 =
= 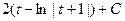 =
= 
 , нужно в подынтегральной функции поискать производную какой-нибудь её части.
, нужно в подынтегральной функции поискать производную какой-нибудь её части. =
=  =
=  =et+C=esin x+C
=et+C=esin x+C
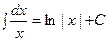
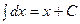



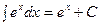


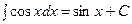


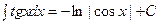
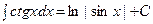
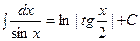


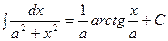
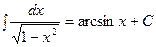
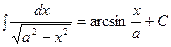






 Þ
Þ  . Проинтегрируем обе части равенства:
. Проинтегрируем обе части равенства: 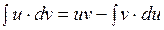 .
. =
=  = =
= =  =
= 
 =
=  =
=  =
= =
= 
 =
=  =
=  = =
= =  =
= 
 =
=  =
=  =
= 
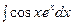 =
=  =
=  = =
= =  =
= 
 ;
;  ;
; 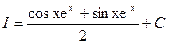
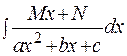 ;
;  .Каждый из указанных двух интегралов берется в два приема:
.Каждый из указанных двух интегралов берется в два приема: ;
; исходный интеграл сводится к табличным интегралам.
исходный интеграл сводится к табличным интегралам. .
.
 .
.
 и
и  .
.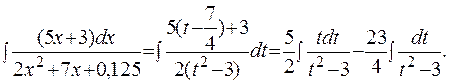

 (тогда
(тогда 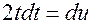 и
и 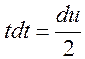 ):
):

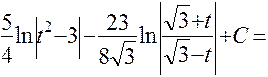


 , где а - вещественное, k, l - натуральные числа, а квадратный трехчлен
, где а - вещественное, k, l - натуральные числа, а квадратный трехчлен 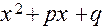 не имеет действительных корней, назовем простейшими сомножителями. Известна основная теорема алгебры: любой многочлен
не имеет действительных корней, назовем простейшими сомножителями. Известна основная теорема алгебры: любой многочлен 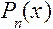 степени n можно разложить в произведение простейших сомножителей:
степени n можно разложить в произведение простейших сомножителей: =
= 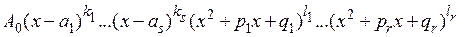 (4)
(4) -число;
-число; 
 , где k, l - натуральные числа,
, где k, l - натуральные числа, 
 - простейший сомножитель, будем называть простейшими рациональными дробями. Используя (4), можно доказать следующую теорему.
- простейший сомножитель, будем называть простейшими рациональными дробями. Используя (4), можно доказать следующую теорему.
 порождает следующую сумму из
порождает следующую сумму из  слагаемых:
слагаемых:  ;
; порождает следующую сумму из
порождает следующую сумму из  слагаемых:
слагаемых: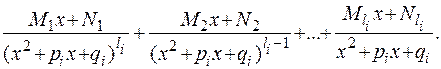
 =
=  +...+
+...+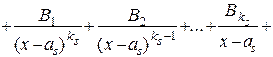 ...+
...+ (5)
(5) на простейшие дроби.
на простейшие дроби. .
.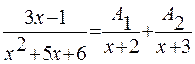 ;
;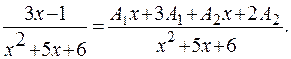
 .
. , следовательно, можно записать следующую систему уравнений:
, следовательно, можно записать следующую систему уравнений: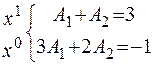 .
.
 .
. на простейшие дроби. Решение:Разложим знаменатель дроби на простейшие сомножители:
на простейшие дроби. Решение:Разложим знаменатель дроби на простейшие сомножители: 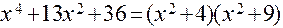 .
. или
или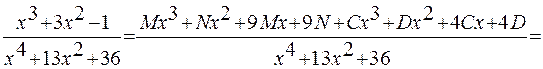
 .
.
 и
и  через
через  и
и  соответственно и подставляя найденные значения в последующие два уравнения, находим:
соответственно и подставляя найденные значения в последующие два уравнения, находим:


 .
.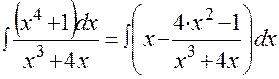
 на простейшие:
на простейшие: ;
;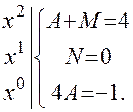 Отсюда
Отсюда 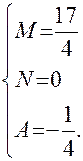



 - рациональная функция своихаргументов. Тогда интеграл
- рациональная функция своихаргументов. Тогда интеграл 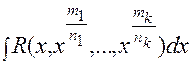 находится заменой переменных
находится заменой переменных 
 берется наименьшее общее кратное чисел
берется наименьшее общее кратное чисел  , где
, где 
 , т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.
, т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались. .
. . Учитывая это, делаем следующую замену переменных:
. Учитывая это, делаем следующую замену переменных: 

 .
.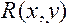 - рациональная функция своих аргументов. Рассмотрим несколько случаев:
- рациональная функция своих аргументов. Рассмотрим несколько случаев: универсальной тригонометри-ческой подстановкой
универсальной тригонометри-ческой подстановкой  сводится к интегралу от рациональной функции. При этом
сводится к интегралу от рациональной функции. При этом  .
.
 ,
, - рациональная функция, интеграл от которой рассматривался выше.
- рациональная функция, интеграл от которой рассматривался выше. .
. .
. .
.


 получим
получим

 =
=  .
. , где
, где 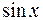 и
и  входят в подынтегральную рациональную функцию, только в четных степенях делается замена
входят в подынтегральную рациональную функцию, только в четных степенях делается замена  . При этом
. При этом .
.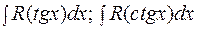 .
.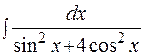 .
.
 .
.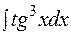 .
.




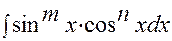 , (6)
, (6)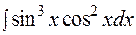 .
.
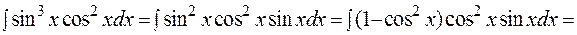
 ;
; .
.


 .
.