
|
|
Теорема об изменении момента количества движения12 Теорема моментов Введем понятие момент количества движения материальной точки, по аналогии с векторным моментом силы (см. раздел «Статика»): момент количества движения (момент импульса) материальной точки относительно центра О есть векторное произведение радиус-вектора на вектор количества движения материальной точки.
Направление и величина момента количества движенияопределяется точно так же, как в случае оценки момента силы (параграф 1.2.2). Одновременно определим главный момент количества движения механической сиситемы как векторную сумму моментов количества движений точек рассматриваемой системы. Он имеет и второе название – кинетический момент механической системы, вычисленный относительно центра О:
вычисленный относительно оси l:
(40) Аналогично осевым моментам силы определяются и осевые кинетические моменты, как проекции главного момента количества движения на оси координат.
Найдем производную по времени выражения (39), используя правила дифференцирования произведения двух функций, а также то, что производная суммы равна сумме производных (т.е. знак суммы при дифференцировании можно перемещать как коэффициент):
Учтем очевидные кинематические равенства:
Применяя ко 2-му слагаемому свойство внутренних сил (34), получим выражение для теоремы об изменении кинетического момента механической системы:
Производная по времени от кинетического момента механической системы, вычисленного относительно некоторого неподвижного центра (О) или неподвижной оси (l), равна сумме моментов всех внешних сил, действующих на систему, вычисленных относительно того же центра или той же оси.
Эту формулировку иногда называют кратко: теорема моментов. Следствие Пусть правая часть выражения (42) равна нулю Для изолированной механической системы вектор кинетического момента системы со временем не меняется ни направлению, ни по величине. Для материальной точки теорема об изменении количества движения читается следующим: производная по времени взятая от момента количества движения материальной точки, вычисленного относительно неподвижного центра (О) или неподвижной оси (l) равна моменту силы, приложенной к материальной точке, вычисленному относительно того же центра или оси. (44)
(45) Кинетический момент твердого тела Рассмотрим частный случай – вращение твердого тела вокруг оси Oz (рис.3).
Рис.3
Точка тела, отстоящая от оси вращения на расстояние hk , вращается в плоскости, параллельной Oxy со скоростью
Введем определение величины осевого момента инерции. Момент инерции тела относительно оси (осевой момент инерции) есть сумма произведений масс точек тел на квадраты расстояний от этих точек до оси.
По теореме Пифагора
Тогда выражение (46) приобретет вид:
Если воспользоваться законом сохранения кинетического момента для частично изолированной системы применительно к твердому телу (47), получим
Осевой момент инерции твердого тела Как мы убедимся впоследствии, осевой момент инерции тела имеет для вращательного движения тела такое же значение, как масса тела при его поступательном движении. Эта одна из важнейших характеристик тела, определяющая инерцию тела при его вращении. Как видно из определения (3.45), эта положительная скалярная величина, которая зависит от масс Для сплошных однородных тел простых форм величину осевого момента инерции, как и в случае оценки положения центра масс(3.8), считают методом интегрирования, используя вместо дискретной массы
Приведем для справки значения моментов инерции для некоторых простых тел:
· Момент инерции тонкого однородного стержня массой m и длиной l относительно оси z, проходящей перпендикулярно стержню через его середину (рис.4).
Рис.4 · Момент инерции тонкого однородного стержня массой m и длиной l относительно оси z, проходящей перпендикулярно стержню через его торец (рис.3.6).
Рис.5 · Момент инерции тонкого однородного кольца массой m и радиусом R относительно оси z, проходящей через его центр перпендикулярно плоскости кольца (рис.6).
Рис.6 · Момент инерции тонкого однородного диска массой m и радиусом R относительно оси z, проходящей через его центр перпендикулярно плоскости диска (рис.7).
Рис.7
· Момент инерции тела произвольной формы. Для тел произвольной формы момент инерции можно представить в такой форме:
где ρ – радиус инерции тела, или радиус некого условного кольца массой m, осевой момент инерции которого равен моменту инерции данного тела.
Теорема Гюйгенса – Штейнера-Эйлера
Рис.8
Свяжем с телом две параллельные системы координат. Первая Cx'y'z', с началом координат в центре масс, называется центральной, и вторая Oxyz, с центром О, лежащей на оси Cx' на расстоянии СО = d (рис.8). Легко установить связи координат точек тела у этих систем: В соответствии с формулой (3.47), момент инерции тела относительно оси Oz:
Здесь постоянные для всех членов 2-й и 3-й сумм правой части сомножители 2d и d вынесены из соответствующих сумм. Сумма масс в третьем слагаемом – это масса тела
Момент инерции тела относительно некой оси равен сумме момента инерции тела относительно параллельной центральной оси, проходящей через центр масс и произведения массы тела на квадрат расстояния между этими осями.
Уравнение динамики вращательного движения твердого тела
Применим теорему моментов для случая вращения тела (43) вокруг оси Oz. Тогда третье уравнение из (43) примет вид:
Первое уравнение – скалярное, второе и третье – дифференциальные уравнения первого и второго порядка, соответственно. На их основе формулируют первую и вторую задачи динамики вращательного движения тела. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.
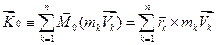 .
.
 . (41)
. (41) . Тогда:
. Тогда:  . Используем среднее уравнение из формул (23)
. Используем среднее уравнение из формул (23)  , а также то, что векторное произведение двух коллинеарных векторов (
, а также то, что векторное произведение двух коллинеарных векторов (  и
и 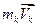 ) равно нулю, получим:
) равно нулю, получим: .
. .
.
 =0, - система изолирована. Тогда из уравнения (42) следует, что
=0, - система изолирована. Тогда из уравнения (42) следует, что  .
.
 . В соответствии с определением осевого момента и заменив проекцию FXY силы на эту плоскость количеством движения точки
. В соответствии с определением осевого момента и заменив проекцию FXY силы на эту плоскость количеством движения точки  . Оценим осевой кинетический момент тела:
. Оценим осевой кинетический момент тела:
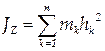
 , поэтому (46) можно записать так:
, поэтому (46) можно записать так:

 . В этом случае можно рассмотреть два варианта:
. В этом случае можно рассмотреть два варианта: ). Тело вращается с постоянной угловой скоростью
). Тело вращается с постоянной угловой скоростью  ;
; . Пример: при исполнении фигуристкой вращения по мере группирования ее тела вблизи вертикальной оси скорость вращения возрастает.
. Пример: при исполнении фигуристкой вращения по мере группирования ее тела вблизи вертикальной оси скорость вращения возрастает. 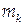 точек системы, но в большей мере от удаленности
точек системы, но в большей мере от удаленности 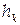 точек от оси вращения.
точек от оси вращения. массу элементарного объема dm=ρdV:
массу элементарного объема dm=ρdV:
 . (49)
. (49)
 .
.
 . (50)
. (50)
 . (51)
. (51)
 , (52)
, (52)


 . Вторая сумма, в соответствии с (7), определяет координату центра масс С на оси Cx' (
. Вторая сумма, в соответствии с (7), определяет координату центра масс С на оси Cx' (  ), причем очевидно равенство:
), причем очевидно равенство:  . Учтя, что 1-е слагаемое, по определению, является моментом инерции тела относительно центральной оси Cz' (или ZC)
. Учтя, что 1-е слагаемое, по определению, является моментом инерции тела относительно центральной оси Cz' (или ZC)  , получим формулировку теоремы Гюйгенса – Штейнера - Эйлера:
, получим формулировку теоремы Гюйгенса – Штейнера - Эйлера:
 . Учитывая определение углового ускорения (2.42), получим 3 варианта уравнения динамики вращательного движения:
. Учитывая определение углового ускорения (2.42), получим 3 варианта уравнения динамики вращательного движения: