
|
|
ПР №10 Экспоненциальное распределение случайной величиныПР №8 Выравнивание вероятностных характеристик Полученная гистограмма не позволяет пока делать каких-либо выводов о плотности вероятностей данной выборки и тем более, генеральной совокупности. Для этого нужна функция, описывающая полученную гистограмму как плотность вероятностей. Процедура выбора этой функции носит название выравнивание. Единого алгоритма выбора выравнивающей функции нет. Подбор функции проводится из различных соображений. Например, во многих случаях природа явлений и внешний вид гистограммы может подсказать одна из известных закономерностей – плотности вероятности. В данном случае природа изучаемого явления и вид гистограммы дают основания для того, чтобы применить плотность нормального распределения вычислим статические оценки – ассиметрии и эксцесса, т.е. центральные моменты:
Если эти величины достаточно малы, то можно ожидать, что плотность вероятностей распределена по нормальному закону. Случайная величина является нормально распределенной, если плотность распределения имеет вид:
где σ и m – статические оценки математического ожидания и дисперсии. Поэтому мы строим эту функцию и проводим сравнение ее графика с гистограммой.
Рисунок 2 – Сравнение гистограммы с графиком функции нормально распределения
Находим критерий согласия Пирсона: - 0,49 Распределение X2 зависит от степени свободы r, которая равна: R = k – число связей В нашем случае число связей = 3, k = 7, тогда: r = 7 - 3 = 4. По таблице находим вероятность появления отклонений P(X2) = 0.5. Полученное значение вероятности нас устраивает, т.к. оно достаточно велико. Можно сделать вывод, что выбранная выравнивающая функция не противоречит статистическому результату.
ПР №9 Определение доверительного интервала Далее нам необходимо определить доверительный интервал (доверительную вероятность). Для выборки в качестве оценок соответствующих величин получены две числовые характеристики:
Эти величины носят название точечных характеристик, т.к. они дают одно значение – точку. Оценка математического ожидания, очевидно, сама является случайной величиной, поэтому ставится задача определения вероятности того, что истинное математическое ожидание накрывается каким-то интервалом около полученной оценки, т.е.:
Вероятность того, что разность между математическим ожиданием m и оценкой математического ожидания Или Отрезок Iβ носит название доверительного интервала, β - доверительной вероятности. Т.е. ставится задача определения попадания истинного математического ожидания m в доверительный интервал около оценки математического ожидания Iβ с вероятностью β. Если бы заранее было известно распределение случайной величины Для получения оценки математического ожидания производится суммирование случайных величин. Эти случайные величины одинаково распределенными. По центральной предельной теореме, как известно, такая сумма при достаточно большом количестве слагаемых близка к нормальному закону и независима от распределения исходной случайной величины. Поэтому для вычисления β воспользуемся законами нормального распределения, взяв для его параметров их оценки. В центральной предельной теореме доказано, что:
В центральной предельной теореме доказано, что:
При: В данном курсовом проекте
В рассматриваемом случае возьмем
Окончательно Оценка доверительного интервала для математического ожидания имеет вид:
Оценка доверительного интервала для дисперсии имеет вид:
ПР №10 Экспоненциальное распределение случайной величины В качестве задания был выдан файл, содержащий нормально распределенные числа (генеральная совокупность). Необходимо осуществить выборку 99 чисел и выбрав функцию распределения, осуществить проверку этого распределения. Получение вариационного ряда В первую очередь, из файла начиная с n⃰⃰ 100 числа ( где n – номер варианта ) провести выборку чисел следующим образом: 1 число получаем как « 0», 1ая цифры, записанные после запятой; 2 число – « 0», 2 ая и 3-я цифры, и т.д. Таким образом выбрать 99 чисел. 0,1,1,2,2,2,7,8,8,9,9,10,12,12,16,20,22,23,24,24,24,24,25,25,26,28,32,33,34,35,35,37,42,44,45,46,47,47,47,48,49,49,50,50,50,54,54,55,55,55,55,55,55,55,57,57,57,57,57,59,62,63,63,64,65,66,70,70,70,71,73,74,75,75,75,75,77,77,78,78,79,79,79,80,82,85,86,87,87,90,91,92,93,93,94,95,97 После этого получить новый вариационный ряд, используя формулу:
Где 𝞴 – 1-ая цифра + 2-ая цифра, т.е 𝞴 = 14, а R𝙞 – Наши полученные 99 чисел.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|





 , которая меньше ε, равна β.
, которая меньше ε, равна β. , Iβ = (
, Iβ = (  )
)

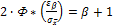 ,
,  ,
, 


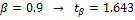



 , тогда:
, тогда:



