
|
|
Вычисление объема тела вращенияРуководство к решению контрольной работы №2 по теме «Интеграл» Неопределенный интеграл. При интегрировании функций наиболее часто используются следующие его свойства: 1) 2) 3) Пример 1. Найти Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:
Ответ: Иногда при интегрировании удобно использовать свойство дифференциала:
Пример 2. Найти Решение. Согласно формуле (2) можно записать:
Теперь воспользуемся свойством 2, а также таблицей интегралов:
Инвариантность формул интегрирования позволяет применять при интегрировании подведение под знак дифференциала части подинтегральной функции, основанное на следующей формуле:
Пример 3. Найти Решение. Воспользуемся методом подведения под знак дифференциала, а также таблицей интегралов:
Ответ: Интегрирование по частям Формулой интегрирования по частям называют следующую формулу: Обычно за Можно выделить два основных класса интегралов, берущихся по частям: 1) – здесь за u принимают многочлен 2) – здесь за u принимают обратную функцию, например, arcsinbx, за Интегрирование рациональных дробей Рациональной дробью
где k, r – целые положительные числа, а трехчлен Интегрирование некоторых тригонометрических функций Для нахождения интегралов видов
Для нахождения интегралов вида
Формула Ньютона–Лейбница Формула Ньютона–Лейбницадля вычисления определенного интеграла имеет вид: если Пример 4. Вычислить определенный интеграл Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона–Лейбница, получаем:
= Ответ: Несобственные интегралы первого и второго рода Интеграл
называется несобственным интегралом первого рода. Интеграл
где a – точка бесконечного разрыва функции Если b – точка бесконечного разрыва функции
– тоже несобственный интеграл второго рода. Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся. Пример 5. Исследовать на сходимость интеграл Решение. Это несобственный интеграл первого рода, поэтому
Следовательно, интеграл сходится и равен Ответ: интеграл сходится и равен Пример 6. Исследовать на сходимость интеграл Решение. Это несобственный интеграл второго рода, так как х = 1 –точка разрыва второго рода подинтегральной функции, поэтому
следовательно, интеграл расходится. Ответ: интеграл расходится. Вычисление площади в декартовой системе координат (ДСК)
Формула для вычисления площади криволинейной трапеции:
9. Вычисление площади в полярной системе координат (ПСК)
Формула для вычисления площади криволинейного сектора: Вычисление объема тела вращения Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b, y = 0 и непрерывной кривой y = f(x), где Если криволинейная трапеция ограничена линиями x = a, x= b,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
; .
. .
. =
=  +3
+3  =
=  .
. . (2)
. (2)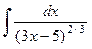 .
.
 .
. Ответ:
Ответ:  .
. . (3)
. (3) .
. =
=  .
. .
. . (4)
. (4) выбирают такое выражение, интегрирование которого не вызывало бы трудностей, а за u – функцию, дифференцирование которой приводит к ее упрощению.
выбирают такое выражение, интегрирование которого не вызывало бы трудностей, а за u – функцию, дифференцирование которой приводит к ее упрощению. ;
;  ;
;  ;
; 
 , за
, за 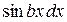 .
. ;
;  ;
; 
 .
. называют отношение двух многочленов
называют отношение двух многочленов  и
и  , т.е.
, т.е.  . Для интегрирования рациональной дроби необходимо предварительно разложить
. Для интегрирования рациональной дроби необходимо предварительно разложить  ,
, не имеет действительных корней. Если дробь
не имеет действительных корней. Если дробь  ), то необходимо предварительно выделить целую часть дроби.
), то необходимо предварительно выделить целую часть дроби. и
и 
 (5)
(5) , где R – рациональная функция (не содержащая sinх и cosx под знаком корней), применяют универсальную подстановку:
, где R – рациональная функция (не содержащая sinх и cosx под знаком корней), применяют универсальную подстановку:  , которая сводит
, которая сводит  и
и  (6)
(6) , (7)
, (7) и
и  непрерывна на
непрерывна на  .
. .
.



 .
. .
.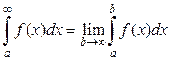 (8)
(8) , (9)
, (9) называется несобственным интегралом второго рода.
называется несобственным интегралом второго рода. , (10)
, (10) .
.

 .
.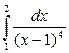 .
.
 ,
, Криволинейной трапецией в ДСК называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой y = f(x), где
Криволинейной трапецией в ДСК называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой y = f(x), где  для
для  (рис. 1).
(рис. 1). . (11)
. (11) Если фигура Ф ограничена в ДСК линиями x = a, x= b, y = f1(x) и y = f2(x) где
Если фигура Ф ограничена в ДСК линиями x = a, x= b, y = f1(x) и y = f2(x) где 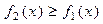 для
для  . (12)
. (12) Криволинейным сектором в ПСК называется фигура, ограниченная лучами
Криволинейным сектором в ПСК называется фигура, ограниченная лучами  и кривой
и кривой  , где
, где  (рис. 3).
(рис. 3). . (13)
. (13) . (14)
. (14) y1 = f1(x) и y2 = f2(x) где
y1 = f1(x) и y2 = f2(x) где  .(15)
.(15)