
|
|
Определение определенного интеграла.Интегрирование функций.
Неопределенный интеграл.
Определение неопределенного интеграла.
Восстановление функции по известной производной этой функции называется интегрированием функции.
Функция F(x) называется первообразной для функции f(x) на некотором отрезке [а;в] если для всех значений х на данном отрезке выполняется равенство F¢(x) = f(x). Множество всех функций, производные которых равны f(x), обозначается символом òf(x)dx
и называется неопределенным интегралом от функции f(x). В данной формуле по определению: f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение. Если F(x) – первообразная для функции f(x), то множество функций F(x) + C будет неопределенным интегралом от функции f(x), т.е.: òf(x)dx = F(x) + C, где С – произвольная постоянная. Свойства неопределенного интеграла.
Из определения неопределенного интеграла вытекают следующие его свойства. 1. Производная неопределенного интеграла равна подинтегральной функции: [òf(x)dx]¢ = [F(x) + C] = F¢(x) = f (x)
2. Постоянный множитель можно выносить за знак неопределенного интеграла: òK f(x)dx = K òf(x)dx 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: òdF(x) = F(x) + C 4. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности: ò(f(x) ± g(x))dx = òf(x)dx ± òg(x)dx
Таблица основных интегралов.
Нижеприведенная таблица неопределенных интегралов получена либо из сравнения с таблицей производных из понимания того, что интегрирование – процедура, обратная дифференцированию, либо непосредственным дифференцированием правой части формулы. Таблица очень краткая и приведена в качестве иллюстрации.
Основные методы интегрирования.
Нахождение неопределенного интеграла – сложная математическая задача, нет единого универсального метода, который позволил бы решить данную задачу. По алгебраическому виду интеграла его можно отнести к определенному классу интегралов, для которых метод нахождения неопределенного интеграла разработан. Хотя существует много различных методов интегрирования, все они основаны на преобразовании (приведении) первоначального интеграла к табличному виду. Рассмотрим некоторые из простых методов.
Метод интегрирования по формулам.
Способ нахождения неопределенных интегралов методом непосредственного использования таблицы интегралов в литературе по математическому анализу имеет несколько названий: непосредственное интегрирование, метод тождественных преобразований, метод интегрирования по формулам. Как правило, для того, чтобы привести интеграл к табличному виду, с первоначальным интегралом òf(x)dx необходимо проделать несложные тождественные преобразования.
Приведем несколько примеров.
1. ò(3cos x + 4x3 – ex )dx = ò3cos x dx + ò4x3 dx - òex dx = 3sin x + x4 - ex +C
2.
3.
=
Правильность интегрирования проверяется дифференцированием найденного неопределенного интеграла. Производная должна быть равна подитегральной функции. Проверка основана на свойстве равенства
F¢(x) = f(x).
Метод замены переменных.
В некоторых случаях введение новой переменной интегрирования x = j(t) позволяет свести неопределенный интеграл
òf(x)dx (1)
к табличному виду. Такой метод называется методом подстановки или методом замены переменной. Алгоритм метода замены переменной для неопределенного интеграла следующий: 1. Введем новую переменную x = j(t) которая должна свести интеграл (1) к табличному виду. Решая данное уравнение относительно t имеем:
t = ψ(x)
2. В первоначальном интеграле (1) сделаем замену переменных: f (x)= dx = j¢(t)dt
3. Интеграл (2) должен решаться в силу основного свойства подстановки x = j(t): данная подстановка должна сводить первоначальный интеграл к табличному виду. Решение интеграла (2) имеет следующий вид:
4. В интеграле (3) сделаем замену переменных t = ψ(x), то есть возвращаемся к первоначальной переменной х: F(t) + C = F(ψ(x)) + C ( 4 ) Для того, чтобы убедиться в том, что найденный интеграл (4) найден правильно, можно продифференцировать выражение (4) и сравнить с подинтегральной функцией интеграла (1). Подинтегральная функция f(x) должна совпадать с производной F¢(ψ(x)):
F¢(ψ(x)) = f(x).
3.4.3. Примеры нахождения неопределенного интеграла.
В данном примере один и тот же интеграл решен двумя разновидностями метода подстановки. Найти неопределенный интеграл
1 способ.
1. 1.1. Делаем замену переменных: t = cos x 1.2. Выражаем старую переменную через новую: x = arccos t 1.3. По определению дифференциала: dx = j¢(t)dt = (arccos t )′ dt = dx=
1.4. sin2x + cos2x = 1, т.к. t = cos x, то sin2x + t2 = 1, sin x = 1.5. Заменяем в первоначальном интеграле cos x, sin x, dx через t. 1.6. Первоначальный интеграл свелся к табличному относительно t. Найти интеграл относительно t . 1.7. При использовании метода подстановки надо помнить, что после взятия неопределенного интеграла необходимо возвращаться от новой переменной t к первоначальной переменной x. Возвращаемся от переменной t к переменной х.
2 способ.
2. 2.1. Вводим переменную t = cos x 2.2. Берем дифференциал от обеих частей и находим dx: dt = - sin x dx sin x dx = - dt dx = - dt/ sin x 2.3. Подставляем вместо cos x и dx их выражения через t в первоначальный интеграл и сводим его к табличному.
Определенный интеграл.
Определение определенного интеграла. Пусть на отрезке [а; в] определена непрерывная функция f(x). Отрезок [а; в] разобьем на частичные отрезки Dx = xi+1- xi. Выберем на каждом отдельном отрезке Dxi произвольным образом точку ti и составим сумму: S = Если существует предел I=
По определению функция f(x) называется подинтегральной функцией, f(x)dx – подынтегральным выражением, a и b – пределы интегрирования (a – нижний предел, b – верхний предел). Геометрически определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), снизу – отрезком [a; b] оси ОХ, с боков отрезками прямых х =а и х = b.
Рис. 2

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



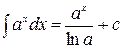

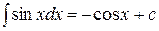

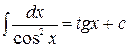








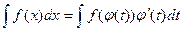 ( 2 )
( 2 ) ( 3 )
( 3 )
 = -
= - 
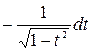



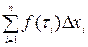
 , то функция f(x) называется интегрируемой на отрезке [а; в], а число I называется определенным интегралом функции f(х) на отрезке [а; в] и обозначается символом:
, то функция f(x) называется интегрируемой на отрезке [а; в], а число I называется определенным интегралом функции f(х) на отрезке [а; в] и обозначается символом:
