|
|
Линейные уравнения второго порядка.Лекция 13. Дифференциальные уравнения и методы их решения В данной лекции рассматриваются следующие вопросы: 1. Основные понятия и определения. 2. Дифференциальные уравнения первого порядка с разделяющимися переменными. 3. Линейные уравнения второго порядка. Изучение данных вопросов необходимо для изучения динамики точки, твердого тела и системы.
Основные понятия и определения. Дифференциальным называется уравнение, содержащее производные неизвестной функции. Обыкновеннымназывается такое дифференциальное уравнение, в котором неизвестная функция зависит от одного аргумента, например,
Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в него (уравнение (1) – уравнениевторого порядка). Решением дифференциального уравнения называется функция, при подстановке которой в это уравнение последнее обращается в тождество. Частным решением дифференциального уравнения называется любое из возможных его решений. Например, подстановкой в уравнение (1) значения x = А легко убедиться, что оно обращается в тождество при x = А = В/k2. Это и есть одно из его частных решений. Общим решениемдифференциального уравнения называется совокупность всех его частных решений. Если уравнение второго порядка является интегрируемым, т.е. его общее решение можно записать в известных функциях, то оно будет иметь вид:
Дифференциальные уравнения первого порядка с разделяющимися переменными. Если дифференциальное уравнение может быть представлено в виде Р(x)dx = Q(t)dt, где функция Р(x) зависит только от x, а функция Q(t) зависит только от t, то говорят, что переменные разделяются. В этом случае имеем
Пример 1. Точка движется прямолинейно со скоростью V = gt (V в м/c, t в c). Найти закон ее движения, если при t = 0 x0 = 1 м. Решение. Так как
и движение точки описывается дифференциальным уравнением с разделяющимися переменными: dx = gtdt.В результате интегрирования получаем: x = gt2/2 + C. Подставив в это уравнение начальное условие x0 = 1 м при t = 0, получим: С = 1 м. Следовательно, закон движения точки имеет вид: x = (gt2/2 + 1) м. Пример 2. Точка движется прямолинейно со скоростью V = 5x (м/c). Найти закон движения точки, если при t = 0 x0 = e (м). Решение. Так как
В результате интегрирования получаем: ln x = 5t + C. Используя начальные данные, находим постоянную: С = ln e = 1 м. Следовательно, закон движения точки имеет вид x = e5t+1 (м).
Линейные уравнения второго порядка. Линейным уравнением второго порядка называется уравнение вида
Если правая часть в этом уравнении равна нулю, т.е. R(t) = 0, уравнение называется однородным, в противном случае – неоднородным. Общее решение неоднородного уравнения (2) x(t) складывается из общего решения x1(t) соответствующего однородного уравнения и какого-либо частного решения x2(t) неоднородного уравнения (2) x(t) = x1(t) + x2(t). (3) Для выполнения индивидуальных заданий необходимо уметь решать дифференциальное уравнение вида
которое является линейным неоднородным уравнением второго порядка с постоянными коэффициентами. Для нахождения общего решения дифференциального уравнения (4) необходимо знать общее решение однородного линейного уравнения x''(t) + 2bx'(t) + k2x(t) = 0, (5) которое ищется в виде
При решении данного уравнения возможны три случая: 1) k < b, когда характеристическое уравнение (6) имеет два неравных действительных корня
2) k = b, когда характеристическое уравнение (6) имеет два равных корня
3) k> b, когда характеристическое уравнение (5) имеет два комплексных корня
Далее, используя формулу Эйлера,
где D1, D2 – некоторые постоянные. В частном случае, когда b = 0 и
Для нахождения общего решения неоднородного дифференциального уравнения (4) необходимо еще найти какое-либо его частное решение. В индивидуальных заданиях встречаются варианты, в которых R(t)=A=const и R(t)=Acos(pt+ В случае, когда R(t)=Acos(pt+ Пример 3. Решить уравнение
В случае, когда
то
Подставляя эти функции в уравнение, находим
Отсюда, учитывая, что Это уравнение удовлетворяется тождественно, если
Следовательно, в данном случае общее решение имеет вид
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
, где С1 и С2 – некоторые постоянные, x – искомая функция аргумента t. Разные значения С1 и С2 дают разные частные решения. В механике обычно требуется найти частное решение дифференциального уравнения, у которого при 
. С этой целью данные подставляются в общее решение. В результате для определения постоянных С1 и С2 получается два уравнения
.
(2)
. В результате его подстановки в уравнение (5) получается характеристическое уравнение
. (6)
. В этом случае имеется два линейно независимых решения и общее решение уравнения (5) является их линейной комбинацией
; (7)
. Общее решение тогда имеет вид
x1; (8)
. Общее решение уравнения (5) снова является линейной комбинацией соответствующих частных
. (9)
, можно показать, что решение (9) сводится к следующему
, (9а)
, общее решение уравнения (5) принимает вид
. (10)
). В первом случае частное решение уравнения (4) можно искать в виде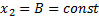 
. Действительно, подставив это выражение в уравнение (4), убеждаемся, что при B=A/k2 оно удовлетворяется при любом t.
, частное решение можно искать в виде: 
, где K и 
– постоянные. Если же R(t)=Acos(pt+ 
.
. Однородное уравнение здесь имеет решение (см. (10))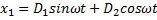 
. Частное решение при 
ищем в виде: 
. Подставляя это выражение в уравнение и учитывая, что 
, находим: 
. Следовательно, общее решение данного уравнения имеет вид
, частное решение будем искать в виде 
. Поскольку
.
и K=-h/2p.