|
|
Силы в трехфазной системе проводниковТема: Электрические станции и подстанции Лекция№10. ЭЛЕКТРОДИНАМИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ ПРОВОДНИКОВ С ТОКАМИ В СХЕМАХ ЭНЕРГОУСТАНОВОК. Оглавление 10.1 Силы взаимодействия двух проводников. 1 10.2 Силы в трехфазной системе проводников. 3 10.3 Электродинамическая стойкость жёстких проводников. 4 10.4 Выбор изоляторов. 5 10.5 Электродинамическая стойкость гибких проводников. 6 10.6 Электродинамическая стойкость аппаратов. 7
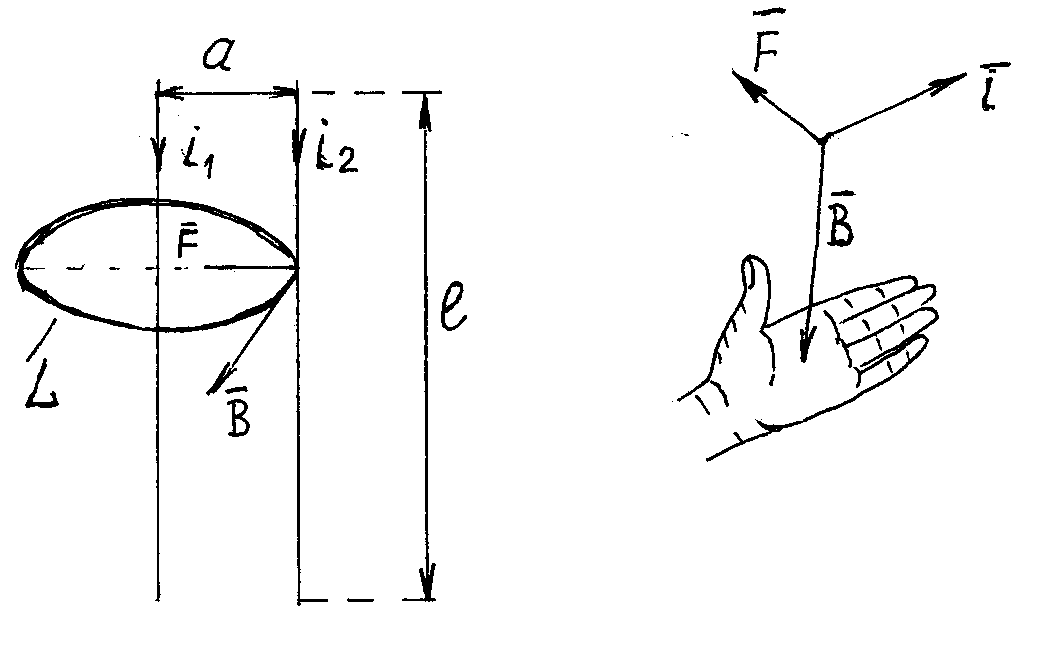
При КЗ проводники и аппараты подвергаются воздействию значительных электродинамических сил, которые могут достигать 4000 – 16000 Н. Эти силы могут вызвать остаточную деформацию жёстких проводников , схлестывание гибких проводников, вызвать отказ во включении выключателей или самопроизвольное отключение разъединителей. Чтобы этого не случилось, все системы токоведущих частей и электрические аппараты проверяются на электродинамическую стойкость при проектировании первичной электрической схемы. Из физики известно, что на элемент проводника dl с токомiв магнитном поле с индукцией Bдействует сила dF=iBdlsinα. Магнитное поле может быть создано другим проводником с током, тогда говорят о взаимодействии двух проводников с токами. Магнитную индукцию от проводника с током можно определить с помощью закона Био-Савара, но иногда бывает удобнее определить В с помощью закона полного тока: Силы взаимодействия двух проводников. Часто взаимодействие между проводниками в схемах энергоустановок сводится к взаимодействию двух параллельных проводников с токами. Рассмотрим этот случай подробнее (Рис.10.1). Пусть проводники длиной l находятся на расстоянии а. Ток в одном проводнике i1 , в другом i2. Будем считать, что l»а (это часто имеет место на практике), тогда для вычисления индукции В1 от первого проводника в районе второго воспользуемся законом полного тока.
Рис. 10.1 Взаимодействие двух проводников с токами и определение направления силы с помощью правила левой руки
В качестве контура интегрирования L выберем окружность с радиусом а. Тогда получим
В нашем случае sin α=1, т.к. α=π/2, поэтому сила, действующая на весь второй проводник:
В практических расчетах динамической стойкости пользуются понятием погонной силы fпог=F/l [Н/м]. Для нашего случая с учётом того, что μ0=4π10-7Гн/м, выражение для погонной силы примет вид:
Т.е. погонная сила пропорциональна произведению токов во взаимодействующих проводниках и обратнопропорциональна расстоянию между ними. В предыдущих формулах предполагалось, что взаимодействующие проводники бесконечно тонкие. Для проводников конечного сечения:
Силы в трехфазной системе проводников Рассмотрим наиболее частый случай, когда проводники фаз располагаются в одной плоскости (Рис.10.2).
Рис. 10.2 Силы в трёхфазной системе токов.
В фазных проводниках протекают токи, которые представляют собой синусоиды с амплитудами Im:
Сила, действующая на проводник средней фазы, больше сил действующих на крайние фазы, поэтому рассмотрим силу, действующую на среднюю фазу. Эта сила будет складываться из двух сил – силы действующей на фазу b со стороны фазы a и силы действующей на фазу b со стороны фазы c:
Окончательно, с учетом формулы двойного угла и коэффициента кф, для погонной силы, действующей на среднюю фазу, можно записать:
В переходном процессе КЗ наибольшее мгновенное значение тока равно его ударному значению iу, поэтому приближенно можно записать:
Наибольшие усилия между проводниками возникают при трёхфазном КЗ, поэтому этот вид КЗ является расчётным при проверке проводников и аппаратов на электродинамическую стойкость. 10.3 Электродинамическая стойкость жёстких проводников. Электродинамическая стойкость жёстких проводников будет обеспечена, если будет выполнено условие: σрасч≤σдоп. Здесь расч – расчётное механическое напряжение в материале проводника; доп – допустимое механическое напряжение в материале проводника (согласно ПУЭ доп=0,7 разр). В качестве примера рассмотрим расчёт электродинамической стойкости проводников из жёстких однополосных шин (Рис.10.3). Жёсткие шины, как правило, жестко крепятся только к одному изолятору в пролёте. На остальных изоляторах шины крепятся с помощью накладок, обеспечивающих возможность продольного перемещения шин. Это необходимо для того, чтобы не развивались механические напряжения в шинах и изоляторах при изменении температуры. Расчет проводится для фазы b, причём т.к. в практических конструкциях a»b+h, то kф=1. Равномерно распределенная сила
Рис. 10.3 Динамическая стойкость жёстких шин: а – расстояние между фазами; l – расстояние между изоляторами; b,h – размеры сечения проводника
Воздействие момента вызывает в материале шин механическое напряжение Т.к. Из условия σрасч=σдоп можно определить пролет, который будет удовлетворять условию электродинамической стойкости для жёсткой однополосной шины:
Полученная формула справедлива при статическом действии силы. Но, как отмечалось выше, электродинамическая сила является переменной во времени. Это может привести к механическому резонансу в системе жесткие шины-изоляторы, когда собственные частоты системы будут близки к 50 и 100 Гц. Если же собственные частоты системы будут меньше 30 или больше 200 Гц, то механический резонанс не возникает и проверка шин на электродинамическую стойкость производится как в статическом случае. Частота собственных колебаний можно вычислить на основе следующих выражений: - для алюминиевых шин - для медных шин Изменяя l, добиваются того, чтобы механический резонанс был исключен, и одновременно выполнялось условие (1). Если только вариация l не позволяет выполнить требуемые условия, то изменяют еще и форму сечения шины. 10.4 Выбор изоляторов Т.к. шины крепятся на опорных изоляторах, то необходима проверка их электродинамической стойкости (Рис.10.4). В общем случае выбор опорных изоляторов производится по следующим условиям: · по номинальному напряжению Uуст≤Uном; · по электродинамической стойкости Fрасч≤Fдоп, где Fрасч – сила, действующая на изолятор; Fдоп – допустимая нагрузка на головку изолятора (Fдоп=0,6Fразр, Fразр – разрушающая нагрузка на изгиб). При горизонтальном или вертикальном расположении изоляторов расчетная сила Fрасч=fbmlkh, где kh – поправочный коэффициент на высоту шины
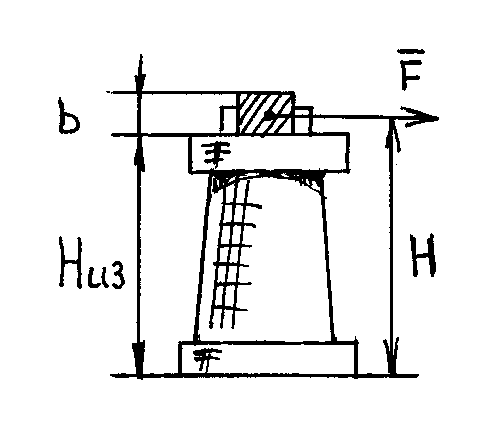
Рис. 10.4 Динамическая стойкость опорного изолятора.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.
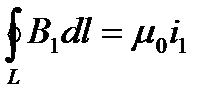 , т.к. в силу симметрии В1=const на контуре L, то можно записать
, т.к. в силу симметрии В1=const на контуре L, то можно записать 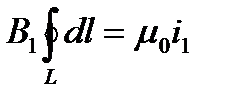 . Из последнего выражения можно записать для индукции от первого проводника в районе второго:
. Из последнего выражения можно записать для индукции от первого проводника в районе второго: 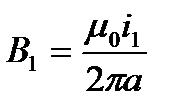 . Зная индукцию В1, можно определить силу dF2 действующую на элемент dl2 второго проводника с током i2.
. Зная индукцию В1, можно определить силу dF2 действующую на элемент dl2 второго проводника с током i2.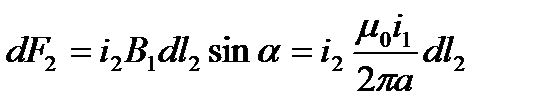 .
.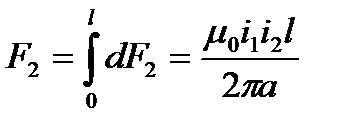 .
.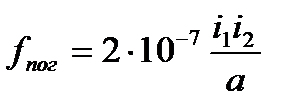 .
.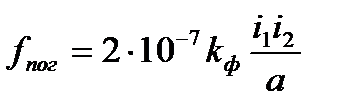 , где кф – коэффициент формы проводника, значения которого приводится в справочниках.
, где кф – коэффициент формы проводника, значения которого приводится в справочниках.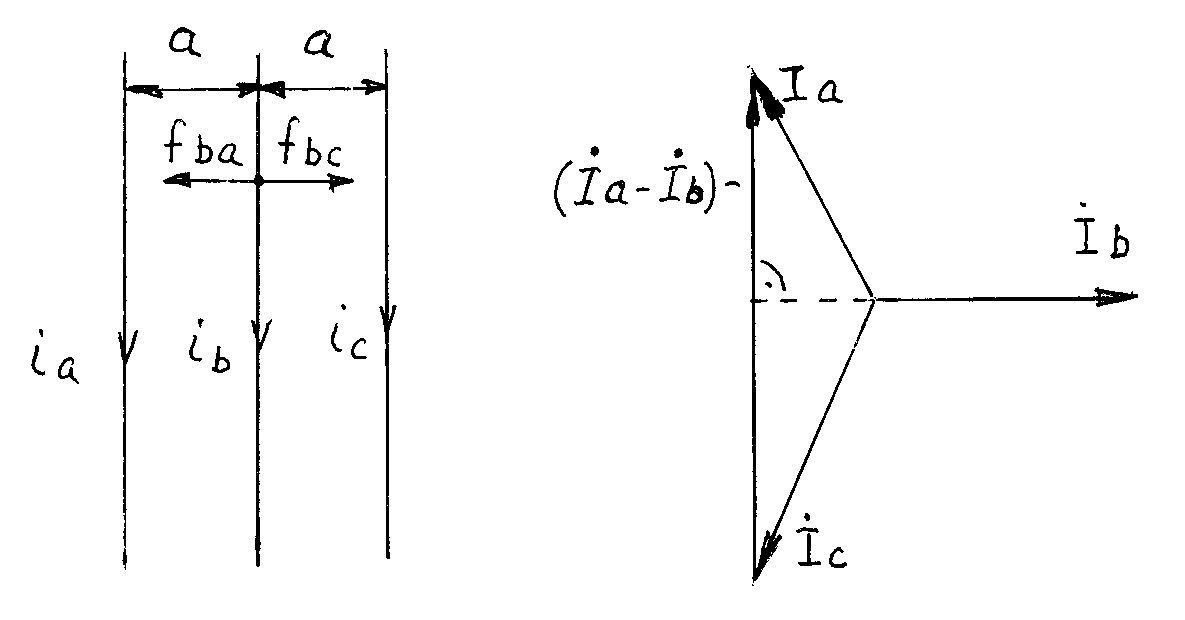
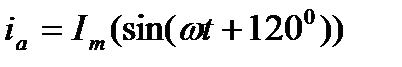
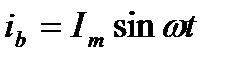
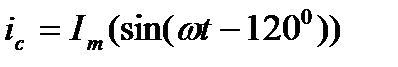 .
.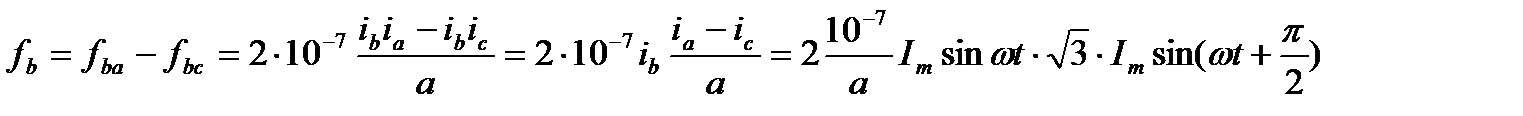 .
.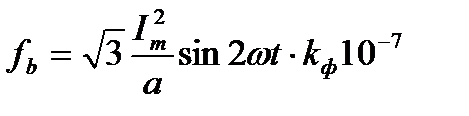 . Таким образом, сила изменяется с частотой в два раза большей частоты сети. Максимальное значение погонной силы будет равно:
. Таким образом, сила изменяется с частотой в два раза большей частоты сети. Максимальное значение погонной силы будет равно: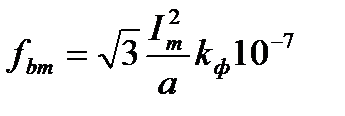 .
.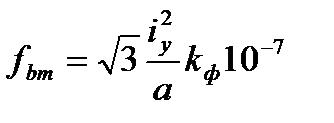 .
.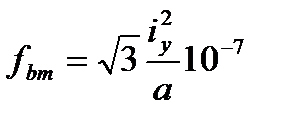 создаёт изгибающий момент
создаёт изгибающий момент 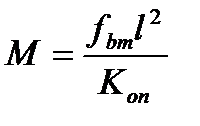 , где Коп – коэффициент, зависящий от способа закрепления шин на опорных изоляторах. На основе практики в общем случае принимают Коп=10.
, где Коп – коэффициент, зависящий от способа закрепления шин на опорных изоляторах. На основе практики в общем случае принимают Коп=10.
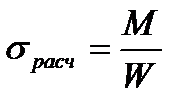 , где W – момент сопротивления шины относительно оси, перпендикулярной действию силы [м3]. W зависит от формы и соотношения размеров в сечении проводника. В нашем случае
, где W – момент сопротивления шины относительно оси, перпендикулярной действию силы [м3]. W зависит от формы и соотношения размеров в сечении проводника. В нашем случае  ,
, 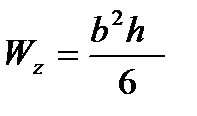 .
.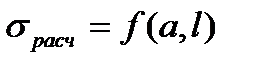 , то, изменяя a и l, добиваются выполнения условия σрасч≤σдоп. Увеличение а приводит к возрастанию габаритов установки, поэтому чаще прибегают к уменьшению l.
, то, изменяя a и l, добиваются выполнения условия σрасч≤σдоп. Увеличение а приводит к возрастанию габаритов установки, поэтому чаще прибегают к уменьшению l.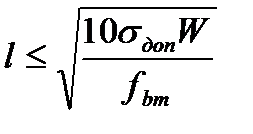 . (1)
. (1)
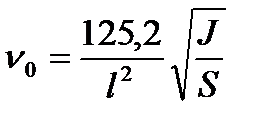 , где l – расстояние между изоляторами, м; J – момент инерции поперечного сечения шины относительно оси, перпендикулярной направлению изгибающей силы, см4; S – площадь сечения шины, см2.
, где l – расстояние между изоляторами, м; J – момент инерции поперечного сечения шины относительно оси, перпендикулярной направлению изгибающей силы, см4; S – площадь сечения шины, см2.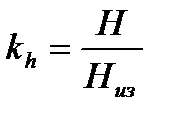 ,
, 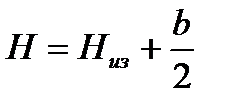 , где Низ – высота изолятора.
, где Низ – высота изолятора.