
|
|
Исследование кривой второго порядка.Классификация кривых второго порядка В зависимости от значения инварианта
Кривая второго порядка называется центральной, если Кривые эллиптического и параболического типа являются центральными кривыми. Центром кривой второго порядка Г называется такая точка плоскости, по отношению к которой точки этой кривой расположены симметрично парами. Точка
Если линия — эллипс и
определяет угловой коэффициент большей оси эллипса. Если уравнение
дает угловой коэффициент вещественной оси гиперболы. Расположение параболы относительно начальной системы координат будет известно, если будут известны вершины параболы, вектор, направленный по ее оси в сторону вогнутости, и параметр. Вершина параболы определяется при решении уравнения оси параболы
или
Совместно с уравнением параболы Вектор
параллелен оси параболы и направлен в сторону ее вогнутости. Параметр параболы определяется по формуле:
Приведение к каноническому виду уравнения кривой второго порядка Если кривая Г задана в декартовой прямоугольной системе координат I. Приведение к каноническому виду уравнения центральной кривой Пусть дано уравнение, определяющее центральную кривую второго порядка:
а) Совершим параллельный перенос начала координат в точку
Подставляя выражение
Раскрывая скобки и приводя подобные члены, получим
В уравнении коэффициенты при
которая определяет координаты центра исходной кривой. Решим эту систему и найдем координаты центра
Отметим, что при параллельном переносе начала координат старшие коэффициенты б) Если При повороте осей координат на угол
Подставляя
Раскроем скобки:
Приводя подобные члены, получим уравнение
Выберем угол
Это требование эквивалентно уравнению
После поворота на угол
Не будет содержать слагаемое с произведением
Выведем следующие обозначения для коэффициентов:
Получим уравнение
Соответствующее одному из канонических уравнений (см. «Теорему 1»).
Замечание 1. Корни Замечание 2. Значения
Замечание 3. Угол
Исследование кривой второго порядка.
Ø Определим зависимость типа кривой второго порядка, заданной уравнением
от параметра Решение. Для уравнения (1) имеем:
В соответствии с классификацией кривых второго порядка: I. Если Но при этом II. Если 1. Если Но при этом 2. Если Следовательно, если а) Если
Следовательно, если б) Если
Следовательно, если Используя полученные результаты, построим таблицу:
Ø Дано уравнение кривой второго порядка
Требуется: 1. Определить тип кривой с помощью инвариантов. 2. Решить характеристическое уравнение, записать каноническое уравнение и определить расположение кривой. 3. Построить каноническую систему координат и кривую в общей системе координат. 4. Привести уравнение кривой к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.
1.Определим тип кривой (2) с помощью инвариантов. Для уравнения кривой второго порядка (2) имеем:
Вычислим инварианты кривой
Так как В соответствии с классификацией кривых второго порядка, так как 2a) Определим расположение данной кривой. Расположение гиперболы, относительно начальной системы координат будет известно, если будут известны координаты центра и угловой коэффициент вещественной оси гиперболы. Уравнения для определения координат центра данной кривой имеют вид:
Решив данную систему, получим координаты центра данной кривой: Угловой коэффициент оси
3. Напишем уравнение осей новой системы координат Так как система В пункте 2 установлено, что угловой коэффициент оси Так как ось Используя полученную информацию, построим каноническую систему координат
4. Приведем уравнение кривой (2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая – центральная, поэтому используем методику к каноническому виду для уравнения центральной кривой.
a) Совершим параллельный перенос начала координат в точку
Подставляя эти выражения в уравнение (2), получим:
Раскрывая скобки и приводя подобные члены, получим уравнение координат
б) Так как
Подставляя (4) в уравнение кривой (3), получим:
Раскроем скобки:
Приводя подобные члены, получим уравнение
Выберем угол
Это требование эквивалентно уравнению
Решая уравнение (7), получим
В пункте 2 установлено, что угловой коэффициент вещественной оси
Подставляя эти значения в уравнение (6), получим
т.е. преобразованное уравнение будет иметь вид
и, соответственно, уравнение
— это каноническое уравнение исходной гиперболы. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 принята следующая классификация кривых второго порядка:
принята следующая классификация кривых второго порядка: кривая эллиптического типа;
кривая эллиптического типа; кривая параболического типа;
кривая параболического типа; кривая параболического типа.
кривая параболического типа.
 является центром кривой второго порядка, определяемой уравнением
является центром кривой второго порядка, определяемой уравнением  в том и только в том случае, когда ее координаты удовлетворяют уравнениям
в том и только в том случае, когда ее координаты удовлетворяют уравнениям
 —меньший по абсолютной величине корень характеристического уравнения, то формула
—меньший по абсолютной величине корень характеристического уравнения, то формула
 — корень характеристического уравнения, знак которого совпадает со знаком
— корень характеристического уравнения, знак которого совпадает со знаком  то формула
то формула





 уравнением
уравнением  то, применяя преобразования поворота осей координат и переноса начала координат, можно привести это уравнение к каноническому виду.
то, применяя преобразования поворота осей координат и переноса начала координат, можно привести это уравнение к каноническому виду. При этом координаты
При этом координаты  произвольной точки
произвольной точки  плоскости в системе координат
плоскости в системе координат  в новой системе координат
в новой системе координат  связаны соотношениями
связаны соотношениями
 в уравнение
в уравнение

 +
+
 приравниваем нулю. Получим систему уравнений относительно
приравниваем нулю. Получим систему уравнений относительно 



 не изменяются.
не изменяются. то дальнейшее упрощение уравнения достигается при помощи поворота осей координат на угол
то дальнейшее упрощение уравнения достигается при помощи поворота осей координат на угол 
 координаты
координаты  в новой системе координат
в новой системе координат  связаны соотношениями
связаны соотношениями
 в уравнение кривой, получим
в уравнение кривой, получим

 +
+ +
+



 равен нулю:
равен нулю:
 .
.
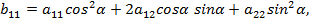



 квадратичного уравнения соответствуют двум взаимно перпендикулярным направлениям (так как по теореме Виета
квадратичного уравнения соответствуют двум взаимно перпендикулярным направлениям (так как по теореме Виета  Поэтому вибирая
Поэтому вибирая 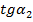 вместо
вместо  , мы только меняем ролями оси
, мы только меняем ролями оси 
 выражаются через
выражаются через  по формулам
по формулам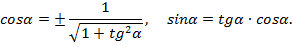
 которое следует из равенства
которое следует из равенства  (1)
(1) с помощью инвариантов
с помощью инвариантов








 , то уравнение (1) определяет кривую параболического типа. Но
, то уравнение (1) определяет кривую параболического типа. Но  , следовательно, если
, следовательно, если  , то уравнение (1) определяет кривую параболического типа.
, то уравнение (1) определяет кривую параболического типа. , следовательно, если
, следовательно, если  , то данная кривая – центральная.Следовательно, при
, то данная кривая – центральная.Следовательно, при  данная кривая – центральная.
данная кривая – центральная. , то уравнение (1) определяет кривую эллиптического типа. Следовательно, если
, то уравнение (1) определяет кривую эллиптического типа. Следовательно, если  , то данная кривая есть кривая эллиптического вида.
, то данная кривая есть кривая эллиптического вида.  , и в соответствии спризнаком кривых второго порядка (
, и в соответствии спризнаком кривых второго порядка ( 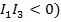 получим:если
получим:если  ), то уравнение (1) определяет эллипс.
), то уравнение (1) определяет эллипс. , то уравнение (1) определяет кривую гиперболического типа.
, то уравнение (1) определяет кривую гиперболического типа. , то уравнение (1) определяет кривую гиперболического типа.
, то уравнение (1) определяет кривую гиперболического типа. , то уравнение (1) определяет две пересекающиеся прямые. Получим:
, то уравнение (1) определяет две пересекающиеся прямые. Получим:
 , то уравнение (1) определяет две пересекающиеся прямые.
, то уравнение (1) определяет две пересекающиеся прямые. , то данная кривая – гипербола. Но
, то данная кривая – гипербола. Но 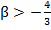 , за исключением точки
, за исключением точки 
 ), то уравнение (1)определяет гиперболу.
), то уравнение (1)определяет гиперболу. 





 (2)
(2)




 то данная кривая – центральная.
то данная кривая – центральная. то данная кривая – гипербола.
то данная кривая – гипербола. (3)
(3) Следовательно, точка
Следовательно, точка  – центр данной кривой.
– центр данной кривой. – вещественной оси гиперболы в соответствии с
– вещественной оси гиперболы в соответствии с
 в исходной системе координат
в исходной системе координат 
 проходят через точку
проходят через точку  .
. Уравнение прямой, проходящей через данную точку
Уравнение прямой, проходящей через данную точку  с заданным угловым коэффициентом
с заданным угловым коэффициентом  имеет вид
имеет вид  Следовательно, ось
Следовательно, ось  в системе координат
в системе координат 
 перпендикулярна оси
перпендикулярна оси  то ее угловой коэффициент
то ее угловой коэффициент  Следовательно, ось
Следовательно, ось  или
или 
 и данную гиперболу в исходной системе координат
и данную гиперболу в исходной системе координат 







 При этом координаты
При этом координаты 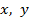 произвольной точки М плоскости в системе координат
произвольной точки М плоскости в системе координат  в новой системе координат
в новой системе координат  связаны соотношениями
связаны соотношениями

 (3)
(3) то дальнейшее упрощение уравнения (3) достигается при помощи поворота осей координат на угол
то дальнейшее упрощение уравнения (3) достигается при помощи поворота осей координат на угол  произвольной точки М плоскости в системе координат
произвольной точки М плоскости в системе координат 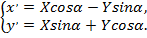 (4)
(4)



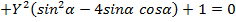 (5)
(5) такой, что в уравнении (5) коэффициент при произведении XY равен нулю:
такой, что в уравнении (5) коэффициент при произведении XY равен нулю: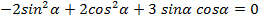 (6)
(6) (7)
(7)
 к оси Ox (а следовательно, и к оси
к оси Ox (а следовательно, и к оси  равен ее угловому коэффициенту (
равен ее угловому коэффициенту (  , то угол поворота
, то угол поворота  выберем такой, что
выберем такой, что 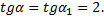 Тогда согласно (7.1) получим:
Тогда согласно (7.1) получим:


