Тема 3. Функции Вебера и Ханкеля.
По определению, цилиндрическая функция есть произвольное решение дифф. уравнения (2.1), поэтому её общее выражение содержится в формуле
 , ,
где  и и 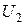 − какие-нибудь линейно независимые решения уравнения (2.1); − какие-нибудь линейно независимые решения уравнения (2.1);  и и  − постоянные, которые могут зависеть от − постоянные, которые могут зависеть от 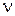 . Для случая, когда . Для случая, когда 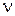 отлично от целого числа, в качестве частных решений уравнения (2.1) можно взять функции Бесселя первого рода порядка отлично от целого числа, в качестве частных решений уравнения (2.1) можно взять функции Бесселя первого рода порядка 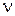 и и 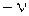 . Для этого необходимо показать, что для нецелых . Для этого необходимо показать, что для нецелых  функции функции  и и  линейно независимы. линейно независимы.
Рассмотрим поведение функции 
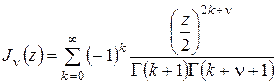 , ,  , ,  . (3.1) . (3.1)
и функции 
 , ,  , ,  . (3.2) . (3.2)
в окрестности начала координат. Если  не равно целому числу, асимптотическое поведение рассматриваемых решений при не равно целому числу, асимптотическое поведение рассматриваемых решений при  будет определяться членами ряда при будет определяться членами ряда при  (когда степень знаменателя максимальна) (когда степень знаменателя максимальна)
 , ,  , ,  . .
Эти формулы верны для всех  за исключением тех значений, когда знаменатель обращается в бесконечность, т.е. за исключением тех значений, когда знаменатель обращается в бесконечность, т.е.  Тогда Тогда
 , ,  . .
Таким образом, функции  и и  будут линейно независимы и общее выражение цилиндрической функции при будут линейно независимы и общее выражение цилиндрической функции при  будет таким: будет таким:
 . (3.3) . (3.3)
Рассмотрим теперь случай, когда  ( (  ). В этом случае ). В этом случае
 , ,
 , ,
поскольку  для всех для всех  и первые и первые  членов для членов для  будут равны нулю. Для этой функции произведём замену переменной суммирования будут равны нулю. Для этой функции произведём замену переменной суммирования  . Получим . Получим
 , , 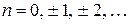 . (3.4) . (3.4)
 Таким образом, функции Бесселя первого рода с целым индексом линейно зависимы и выражение (3.3) не является общим интегралом уравнения Бесселя (2.1) в этом случае. Следовательно, для целых Таким образом, функции Бесселя первого рода с целым индексом линейно зависимы и выражение (3.3) не является общим интегралом уравнения Бесселя (2.1) в этом случае. Следовательно, для целых  надо построить ещё одно решение уравнения Бесселя. надо построить ещё одно решение уравнения Бесселя.
Отметим асимптотические свойства функций Бесселя первого рода при  . Из формулы (3.1) следует (рассматривается только первый член ряда), что . Из формулы (3.1) следует (рассматривается только первый член ряда), что
 , ,  , ,  . (3.5) . (3.5)
Следовательно, функция  ограничена в окрестности начала координат (рис. 2.1). ограничена в окрестности начала координат (рис. 2.1).
Будем предполагать теперь, что 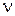 не является целым. Введём в рассмотрение функцию Бесселя второго рода не является целым. Введём в рассмотрение функцию Бесселя второго рода  , которая для произвольных , которая для произвольных  , принадлежащих плоскости с разрезом ( , принадлежащих плоскости с разрезом (  ), определяется выражением ), определяется выражением
 , ,  , ,  . (3.6) . (3.6)
Эта функция для нецелых  является решением уравнения Бесселя (2.1) и линейно независима с функцией Бесселя первого рода является решением уравнения Бесселя (2.1) и линейно независима с функцией Бесселя первого рода  (т. к. в неё входят (т. к. в неё входят  и и  ). Функция (3.6) − это цилиндрическая функция второго рода или функция Вебера. В некоторых работах её обозначают ). Функция (3.6) − это цилиндрическая функция второго рода или функция Вебера. В некоторых работах её обозначают  , а саму функцию называют функцией Неймана. , а саму функцию называют функцией Неймана.
При целом 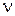 функция Вебера (3.6) приобретает неопределённый вид ( функция Вебера (3.6) приобретает неопределённый вид (  , ,   ). Под значением функции в этом случае понимают предел ). Под значением функции в этом случае понимают предел
 . .
Покажем, что функция  удовлетворяет уравнению Бесселя. Так как числитель и знаменатель в (3.6) − целые функции удовлетворяет уравнению Бесселя. Так как числитель и знаменатель в (3.6) − целые функции 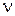 , то рассматриваемый предел существует и может быть вычислен по правилу Лопиталя. Применение этого правила даёт следующее представление: , то рассматриваемый предел существует и может быть вычислен по правилу Лопиталя. Применение этого правила даёт следующее представление:
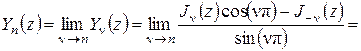
 
 . (3.7) . (3.7)
Для функций  и и  можем записать уравнения Бесселя можем записать уравнения Бесселя
 , ,
 . .
Продифференцировав каждое из этих тождеств по 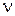 , получим , получим
 , ,  . .
Умножим теперь первое соотношение на 1, а второе − на  и вычтем одно из другого. Получим и вычтем одно из другого. Получим
 . .
Разделим теперь это соотношение на  и перейдём к пределу при и перейдём к пределу при  . С учётом (3.7) и линейной зависимости функций Бесселя при . С учётом (3.7) и линейной зависимости функций Бесселя при  (3.4) получим (3.4) получим
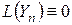 . .
Это и доказывает, что  − решение уравнения Бесселя (2.1). − решение уравнения Бесселя (2.1).
Функции Вебера с целым индексом, также как и функции Бесселя первого рода, линейно зависимы
 , ,  ., (3.8) ., (3.8)
что является следствием представления (3.7) и свойства (3.4).
Для того чтобы получить разложение в ряд функции  , достаточно воспользоваться формулой (3.7) и вычислить производные по индексу , достаточно воспользоваться формулой (3.7) и вычислить производные по индексу 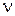 , исходя из разложений (3.1) и (3.2). Найдём эти производные. , исходя из разложений (3.1) и (3.2). Найдём эти производные.


 . .
Тогда  . .
Аналогично  . .
При формировании предельного выражения для этой производной необходимо помнить, что при  (т.е. для первых (т.е. для первых  членов ряда) и членов ряда) и 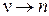 значение значение  и значение и значение  . Поэтому первые . Поэтому первые  членов ряда, содержащих членов ряда, содержащих 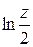 , будут отсутствовать ( , будут отсутствовать (  , при , при  ), а первые ), а первые  членов ряда, содержащих членов ряда, содержащих  , принимают неопределённый вид. Раскроем эту неопределённость. Имеем , принимают неопределённый вид. Раскроем эту неопределённость. Имеем
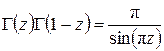   . .
Тогда  . .
Возьмём 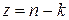 при при  . Тогда с учётом последней формулы получим . Тогда с учётом последней формулы получим
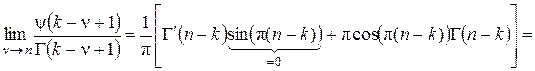
 . .
Таким образом, для предельного выражения второй производной имеем

 . .
или при замене индекса суммирования во второй сумме 

Подставляя найденные производные в формулу (3.7), найдем представление функции Вебера с целым индексом в виде ряда

 , ,  , ,  , ,  (3.9) (3.9)
Если принять во внимание, что  , то это представление верно и для случая , то это представление верно и для случая  . Сравнивая коэффициент при . Сравнивая коэффициент при 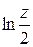 с общим членом ряда в (3.1), можно заключить, что справедливо также и следующее представление в виде ряда: с общим членом ряда в (3.1), можно заключить, что справедливо также и следующее представление в виде ряда:

 , ,  , ,  , ,  (3.10) (3.10)
Полученный результат показывает, что функция Вебера есть регулярная функция в плоскости с разрезом по отрицательной части вещественной оси. Далее,  есть решение, линейно независимое от решения есть решение, линейно независимое от решения  (см. 3.10). (см. 3.10).
Из представления (3.9) вытекает, что при  справедливы следующие асимптотические формулы: справедливы следующие асимптотические формулы:
 , ,  , ,  . (3.11) . (3.11)
Эти формулы показывают, что  , когда , когда  . .
Решения уравнения Бесселя  и и  линейно независимы между собой. Для линейно независимы между собой. Для  этот результат является следствием линейной независимости решений этот результат является следствием линейной независимости решений  и и 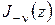 . Линейная независимость для . Линейная независимость для  ( (  ) вытекает из (3.10) или сопоставления поведения рассматриваемых функций при ) вытекает из (3.10) или сопоставления поведения рассматриваемых функций при  (3.5) и (3.11). Таким образом, общее выражение цилиндрической функции, пригодное при любых значениях (3.5) и (3.11). Таким образом, общее выражение цилиндрической функции, пригодное при любых значениях 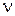 , будет , будет
 . .
В рассмотрение вводят ещё две новые цилиндрические функции
 , (3.12) , (3.12)
 . (3.13) . (3.13)
Это − функции Бесселя третьего рода первого и второго порядка с индексом  , которые называются также функциями Ханкеля первого и второго рода с индексом , которые называются также функциями Ханкеля первого и второго рода с индексом  . Очевидно, что эти функции линейно независимы с функциями Бесселя первого рода и между собой. Они определены для . Очевидно, что эти функции линейно независимы с функциями Бесселя первого рода и между собой. Они определены для  , ,  . .
Асимптотическое поведение функций Ханкеля при  определяется следующими формулами: определяется следующими формулами:
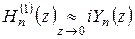 , ,  , ,  . (3.14) . (3.14)
Таким образом, ограниченной при  остаётся только функция Бесселя первого рода. остаётся только функция Бесселя первого рода.
Все цилиндрические функции при фиксированном  есть целые функции параметра есть целые функции параметра 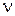 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ,
, и
и 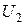 − какие-нибудь линейно независимые решения уравнения (2.1);
− какие-нибудь линейно независимые решения уравнения (2.1);  и
и  − постоянные, которые могут зависеть от
− постоянные, которые могут зависеть от 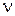 . Для случая, когда
. Для случая, когда 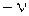 . Для этого необходимо показать, что для нецелых
. Для этого необходимо показать, что для нецелых  функции
функции  и
и  линейно независимы.
линейно независимы.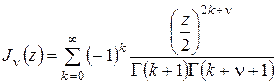 ,
,  ,
,  . (3.1)
. (3.1) ,
,  будет определяться членами ряда при
будет определяться членами ряда при  (когда степень знаменателя максимальна)
(когда степень знаменателя максимальна) ,
,  ,
,  Тогда
Тогда ,
,  .
. . (3.3)
. (3.3) (
(  ). В этом случае
). В этом случае ,
, ,
, для всех
для всех  и первые
и первые  членов для
членов для  будут равны нулю. Для этой функции произведём замену переменной суммирования
будут равны нулю. Для этой функции произведём замену переменной суммирования  . Получим
. Получим ,
, 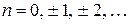 . (3.4)
. (3.4) Таким образом, функции Бесселя первого рода с целым индексом линейно зависимы и выражение (3.3) не является общим интегралом уравнения Бесселя (2.1) в этом случае. Следовательно, для целых
Таким образом, функции Бесселя первого рода с целым индексом линейно зависимы и выражение (3.3) не является общим интегралом уравнения Бесселя (2.1) в этом случае. Следовательно, для целых  ,
,  ,
,  . (3.5)
. (3.5) ограничена в окрестности начала координат (рис. 2.1).
ограничена в окрестности начала координат (рис. 2.1). , которая для произвольных
, которая для произвольных  , принадлежащих плоскости с разрезом (
, принадлежащих плоскости с разрезом (  ), определяется выражением
), определяется выражением ,
,  (т. к. в неё входят
(т. к. в неё входят  , а саму функцию называют функцией Неймана.
, а саму функцию называют функцией Неймана. ,
, 
 ). Под значением функции в этом случае понимают предел
). Под значением функции в этом случае понимают предел .
. удовлетворяет уравнению Бесселя. Так как числитель и знаменатель в (3.6) − целые функции
удовлетворяет уравнению Бесселя. Так как числитель и знаменатель в (3.6) − целые функции 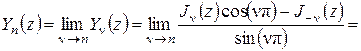


 . (3.7)
. (3.7) ,
, .
. ,
,  .
. и вычтем одно из другого. Получим
и вычтем одно из другого. Получим .
. и перейдём к пределу при
и перейдём к пределу при  . С учётом (3.7) и линейной зависимости функций Бесселя при
. С учётом (3.7) и линейной зависимости функций Бесселя при  (3.4) получим
(3.4) получим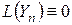 .
. ,
, 

 .
. .
. .
. (т.е. для первых
(т.е. для первых 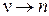 значение
значение  и значение
и значение  . Поэтому первые
. Поэтому первые 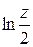 , будут отсутствовать (
, будут отсутствовать (  , при
, при  , принимают неопределённый вид. Раскроем эту неопределённость. Имеем
, принимают неопределённый вид. Раскроем эту неопределённость. Имеем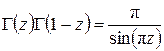

 .
. .
.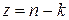 при
при 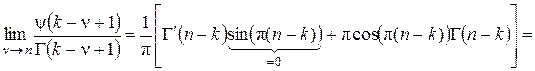
 .
.
 .
.


 ,
,  , то это представление верно и для случая
, то это представление верно и для случая  . Сравнивая коэффициент при
. Сравнивая коэффициент при 
 ,
,  ,
,  , когда
, когда  и
и  линейно независимы между собой. Для
линейно независимы между собой. Для  этот результат является следствием линейной независимости решений
этот результат является следствием линейной независимости решений 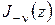 . Линейная независимость для
. Линейная независимость для  .
. , (3.12)
, (3.12) . (3.13)
. (3.13) , которые называются также функциями Ханкеля первого и второго рода с индексом
, которые называются также функциями Ханкеля первого и второго рода с индексом 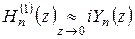 ,
,  ,
,