
|
|
Построение графиков работ сил сопротивления и движущих сил.Построение одномассовой динамической модели машинного агрегата.
В качестве звена приведения выбираем условное звено, совершающее вращательное движение с той же угловой скоростью, что и кривошип. Параметрами модели являются приведенный момент инерции Iп , приведенный момент сил полезного сопротивления Мпс и движущих сил Мпд
Представим Iп в виде сумм двух слагаемых Iп=I1+III где I1 – приведенный момент инерции звеньев, связанных с кривошипом постоянным передаточным отношением; III – приведенный момент инерции остальных звеньев. Приведение масс выполняется из условия равенства кинетической энергии звена приведения сумме кинетических энергий звеньев механизма. Поэтому III подсчитывается для каждого положения механизма по формуле
С использованием планов скоростей формула приобретает следующий вид
III=
где mI и Ii – соответственно массы и моменты инерции звеньев механизма. Отношения скоростей вычисляем, используя построенные ранее планы возможных скоростей. Исходные данные и результаты расчетов заносим в таблицу.
Приведение сил выполняется из условия равенства мощности приведенного момента сумме мощностей всех сил и пар сил, действующих в машинном агрегате. Приведенный момент Мпс сил сопротивления определяется для каждого положения механизма по формуле:
Мпс =
где Gi – сила тяжести соответствующего звена; Fпс- сила производственного сопротивления. Результаты расчета Мпс сводятся в таблицу.
Определение динамического цикла машинного агрегата. Установившимся движением называется такое, при котором скорость начального звена (обобщенная скорость) является периодической функцией времени и координаты. Период изменения скорости начального звена называется динамическим циклом установившегося движения или сокращенно циклом. Параметры динамической модели Мпс и III также являются периодическими функциями угла j со своими, в общем случае разными, периодами. Динамический цикл машинного агрегата будет равен наименьшему общему кратному периодов Мпс и III. Например, если период изменения III соответствует одному обороту кривошипа, а Мпс повторяет свои значения через два оборота, то динамический цикл равен двум оборотам, т.е. j=4p. Для нашего случая параметры модели Мпс и III повторяют свои значения с каждым оборотом кривошипа, поэтому j=2p.
Построение графиков работ сил сопротивления и движущих сил. Наш механизм работает в установившемся режиме, при котором угловая скорость кривошипа есть периодическая функция его угла поворота, а среднее значение угловой скорости не изменяется. Для изучения установившегося движения достаточно рассмотреть его динамический цикл, равный одному обороту кривошипа j=2p. Определим работу
mj=
mМ= 20 Н*м/мм
Для упрощения графического решения и экономии места на чертеже график Мпс(j) строим перевернутым относительно оси абцисс, т.е. отрицательные значения Мпс(j) взятые из ранее полученной таблицы, откладываем в области положительных значений ординат, а положительные – в области отрицательных значений. График Ас получаем путем графического интегрирования построенного графика Мпс(j) при этом масштабный коэффициент полученного графика
mА=mj*mМ*H1=0,0349*20*60=41,88 Дж Суть метода: на продолжении оси абсцисс слева выбирается произвольный отрезок интегрирования ОК, чем он длиннее, тем более пологим будет график А
Построим теперь график изменения работы А
Построим теперь график изменения работы Ад(j) приведенного момента движущих сил. Так как в начале и в конце цикла установившегося движения угловая скорость звена приведения одинакова, то приращение кинетической энергии в этих точках равна нулю, что означает равенство по модулю работ Ас и Ад. График Ад(j) должен пройти через начало и конец графика Ас , построенного за один цикл. Введем допущение, что вращающий момент электродвигателя и, соответственно, приведенный момент Мпд движущих сил есть величины постоянные. Тогда график Ад(j) представляет собой линейную зависимость. Учитывая вышеизложенное, получим график Ад(j), соединив начало и конец графика Ас(j) отрезком прямой. Значение Мпд = const получим, выполнив графическое дифференцирование графика Ад(j)
Выбор электродвигателя. В машинных агрегатах, работающих в установившемся режиме чаще всего применяются асинхронные трехфазные электродвигатели переменного тока серии 4А. Конкретный двигатель выбирается по номинальной мощности Мощность
Потребная мощность двигателя с учетом потерь определяется по формуле:
По каталогу исходя из полученных величин выбираем электродвигатель.
Тип двигателя – НА160S4Y3 Номинальная мощность в кВт-15 Номинальная частота вращения в об/мин – 1465 Синхронная частота вращения в об/ мин – 1500 Момент инерции ротора двигателя
Определение средней частоты вращения кривошипа. Вначале определяем номинальный вращающий момент:
Средний вращающий момент на роторе электродвигателя:
где
Средняя частота вращения ротора определяется по формуле
Таким образом средняя частота вращения кривошипа:
и средняя угловая скорость соответственно:
Определение момента инерции маховика и закона движения звена приведения по методу Н.И.Мерцалова Основное назначение маховика в механизме заключается в обеспечении требуемой неравномерности вращения кривошипа, т.е. в ограничении размаха колебаний угловой скоротси от минимального до максимального значений за цикл установившегося режима, установленным коэффициентом d неравномерности движения. Потребный момент инерции маховика Iм находится по заданному значению коэффициента d с учетом величины средней угловой скорости кривошипа и распределения инерционных и силовых параметров машинного агрегата, учитываемых приведенными моментами инерции и сил. Для синтеза маховика по методу Мерцалова вычисляется кинетическая энергия ТII , Дж звеньев, не связанных с кривошипом постоянным передаточным отношением по формуле
Результаты расчета для каждого положения механизма заносим в таблицу. Выбрав масштабный коэффициент
mТ= 2 Дж/мм строим график ТII(f). Зависимость III (f) имеет такой же вид, так как wср= const , а масштабный коэффициент подсчитывается по формуле
Далее строится зависимость На построенной кривой
Приведенный момент инерции звеньев связанных с кривошипом постоянным передаточным отношением находим по формуле
Значение -приведенный к валу кривошипа момент инерции ротора электродвигателя
-приведенный момент инерции звеньев привода
- момент инерции маховика Поэтому
Закон изменения угловой скорости звена приведения при установившемся движение машинного агрегата совпадает с законом изменения
Линия ,соответствующая на графике Так как начало координат выходит за пределы листа ,то ось абцисс графика
Конструирование маховика и определение места его установки в машинном агрегате. Для уменьшения массы и габаритов целесообразно применять конструкцию маховика в виде тяжелого обода, связанного с нажимаемой на вал ступицей, спицами или облегченным диском. Для такого маховика
Iм=m*D2/4; Ввиду значительной величины момента инерции маховика принимаем решение о его установке на выходном валу редуктора . В этом случае приведенный к выходному валу редуктора момент Инерции маховика определяется по следующей формуле
Определяем требуемый диаметр такого маховика
подставляя получаем
Массу обода определяем по формуле
Масса маховика соответственно
H=0,25D=276*0,25=69 мм В=0,35D=276*0,35=97 мм
СИНТЕЗ МЕХАНИЗМА Принимаем масштаб построения µ1=0,002 В принятом масштабе размечаем Положение центров О и С ,А также линию перемещения звена 5. При этом : Из центра С проводим дугу радиусом Из центра О проводим две дуги ,делая засечки на ранее проверенной дуге :
Соединив полученные точкб с центром С .определяем тем самым крайние положения звена 3. Разбиваем траекторию перемещения т.А на 12частей (через 30°) и методом засечек строим 12 положений механизма . За первое положении принимаем положение при котором механизм начинает холостой ход( усилие нагрузки Fc = 0). ПОСТРОЕНИЕ ПЛАНОВ ВОЗМОЖНЫХ СКОРОСТЕЙ Планы скоростей строим в произвольном масштабе.. Кривошип OA вращается относительно центра О.Принимаем точку р за полюс плана скоростей и приступаем к построению. Откладываем отрезок ра = 60мм _L OA .т.е. направленный в сторону вращения кривошипа .В произвольном масштабе он представляет собой скорость т.А , принадлежащей кривошипу .Для нахождения скости т.В решаем векторное уравнения
Vв- скорость т В. Эта точка принадлежит не только второму ,но и третьему звену находящемуся во вращательно движении .Поэтому VB _L ВС; VА - скорость точки В в переносном движении совместно с точкой А; VBA - скорость точки В в относительном движении относительно точки А. решая это уравнение графически, находим скорость точки В - рb. Для нахождения скорости точки D Составляем векторное уравнение VD =VB+ VDB Здесь: VD- скорость т D. Эта точка принадлежит третьему звену находящемуся во вращательном движении .Поэтому V ┴ ВС ; VD - скорость точки D в переносном движении совместно с точкой В; VDB - скорость точки D в относительном движении относительно точки В. решая это уравнение графически, находим скорость точки D - pd . Для нахождения скорости точки F составляем векторное уравнение V,, =VD+ VFD Здесь: VF- скорость т F. Эта точка принадлежит пятому звену находящемуся в поступательном движении. Поэтому VFIIY - Y ; VD - скорость точки F в переносном движении совместно с точкой D ; VFD - скорость точки F в относительном движении относительно точки D. решая это уравнение графически, находим скорость точки F pf. Для нахождения скоростей центров тяжести звеньев используем теорему о подобии плоской фигуры и планов скоростей .

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|




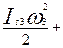


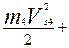
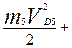
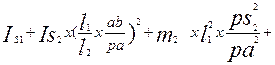
 +
+  +
+ +
+  +
+ 

 приведенного момента Мпс при повороте звена приведения на угол j=2p. Для этого сначала изображаем на чертеже график Мпс. Масштабные коэффициенты принимаем равными
приведенного момента Мпс при повороте звена приведения на угол j=2p. Для этого сначала изображаем на чертеже график Мпс. Масштабные коэффициенты принимаем равными =0,03491 рад/мм
=0,03491 рад/мм . Затем площадь под кривой М(φ1) на каждой итерации заменяется площадью равновеликого прямоугольника.
. Затем площадь под кривой М(φ1) на каждой итерации заменяется площадью равновеликого прямоугольника.

 (j) приведенного момента сил сопротивления. Так как в начале и в конце цикла установившегося движения угловая скорость звена приведения одинакова, то приращение кинетической энергии в этих точках равна нулю, что означает равенство по модулю работ Ас и Ад. График А
(j) приведенного момента сил сопротивления. Так как в начале и в конце цикла установившегося движения угловая скорость звена приведения одинакова, то приращение кинетической энергии в этих точках равна нулю, что означает равенство по модулю работ Ас и Ад. График А  сил сопротивления есть величина постоянная. Тогда график А
сил сопротивления есть величина постоянная. Тогда график А 
 и синхронной частоте
и синхронной частоте  . Обычно выбирается двигатель со средним значением синхронной частоты
. Обычно выбирается двигатель со средним значением синхронной частоты 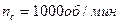
 , приведенного момента
, приведенного момента  на звене приведения вычисляем по формуле
на звене приведения вычисляем по формуле 540*17,8=9608 Вт
540*17,8=9608 Вт
 - 0,41
- 0,41

 - передаточное число привода
- передаточное число привода





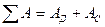 путем сложения с учетом знаков графиков Ад(j) и Ас(j). Затем из графика
путем сложения с учетом знаков графиков Ад(j) и Ас(j). Затем из графика  вычитается график ТII(j). Полученная кривая
вычитается график ТII(j). Полученная кривая  есть зависимость приращения кинетической энергии звеньев механизма, связанных с кривошипом постоянным передаточным отношением.
есть зависимость приращения кинетической энергии звеньев механизма, связанных с кривошипом постоянным передаточным отношением. находим наибольший максимум и наименьший минимум, разность между которыми позволяет вычислить наибольший размах изменений кинетической энергии
находим наибольший максимум и наименьший минимум, разность между которыми позволяет вычислить наибольший размах изменений кинетической энергии
 101*2=202 Дж
101*2=202 Дж
 включает в себя в общем случае
включает в себя в общем случае
 ,учитывающий массы муфт и зубчатых колес привода
,учитывающий массы муфт и зубчатых колес привода ,при его установке на валу кривошипа .
,при его установке на валу кривошипа . 63,11-7,62-5,2=50,3
63,11-7,62-5,2=50,3
 средней угловой скорости строится параллельно оси абцисс и выше на расстоянии a/2 ординаты
средней угловой скорости строится параллельно оси абцисс и выше на расстоянии a/2 ординаты  .
.
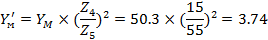
 ,где
,где -плотность материала обода (сталь
-плотность материала обода (сталь 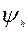 -коэффициент высоты обода (рекомендуется принимать в диапазоне 0,2…..0,4)
-коэффициент высоты обода (рекомендуется принимать в диапазоне 0,2…..0,4) -коэффициент ширины обода (рекомендуется принимать его в диапазоне 0,2...0,4 )
-коэффициент ширины обода (рекомендуется принимать его в диапазоне 0,2...0,4 )

 1,3*196=255 кг
1,3*196=255 кг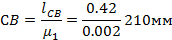


 /VBA Здесь:
/VBA Здесь: