
|
|
Примеры решения типовых задачПример 1. Производная функция (в денежном выражении) имеет вид Решение. Производственная функция в денежном выражении равна доходу от использования ресурсов. Издержки при этом равны
Требуется найти ее максимум. Частные производные функции
Таким образом, найденная критическая точка есть точка максимума. Соответствующее значение прибыли равно Пример 2.Производственная функция равна Решение. Следует максимизировать функцию Итак, имеем задачу максимизации функции
при условии что Первый способ. В силу ограничений имеем Производная функции Второй способ. При условии, что Уравнение линии уровня функции прибыли Легко видеть, что максимальное значение Замечание. Оптимальное решение лежит на прямой ограничений (в данном случае на прямой Пример 3.Функция полезности имеет вид:
Цена единицы первого блага равна 8, второго – 16. На приобретение этих благ может быть затрачена сумма, равная 1000. Как следует распределить эту сумму между двумя благами, чтобы полезность от их приобретения была бы наибольшей? Решение. Рассмотрим линии уровня функции полезности
Таким образом, линии уровня представляют собой графики функции Используя рассуждения, приведенные в предыдущем примере, получаем, что в точке
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1969. – 440с.; 2. Виленкин Н.Я. и др. Задачник по курсу математического анализа, ч.1.– М.: Просвещение, 1971. – 343 с.; 3. Давыдов Н.А. и др. Сборник задач по математическому анализу.–М.: Просвещение, 1973. – 256 с.; 4. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1./ Данко П.Е., Попов А.Г., Кожевникова Т.Я. – М.: ООО «Издательство «Мир и образование», 2003. – 304 с.; 5. Кремер Н.Ш. Высшая математика для экономистов.– М.: ЮНИТИ, 1997. – 479 с.; 6. Кудрявцев Л.Д. Краткий курс математического анализа: В 2-х т.: Т.1. Дифференциальное и интегральное исчисления функции одной переменной. Ряды. – Висагинас: «Alfa», 1998.–400с.; 7. Кудрявцев Л.Д. Краткий курс математического анализа: В 2-х т.: Т.2. Дифференциальное и интегральное исчисления функции многих переменных. Гармонический анализ. – Висагинас: «Alfa», 1998. – 384 с.; 8. Кузнецов Б.Т. Математика. – М.:ЮНИТИ, 2004. – 719 с.; 9. Лекции по математическому анализу / Архипов Г.И. , Садовничий В.А., Чубариков В.Н. – М.: Дрофа, 2003.–640 с.; 10. Малугин В.А. Математика для экономистов: математический анализ. Задачи и упражнения.– М.: Эксмо, 2006. – 288 с.; 11. Марон И. А. Дифференциальное и интегральное исчисление в примерах и задачах функции одной переменной. – М.: Наука, 1973.– 375 с.; 12. Математический анализ в вопросах и задачах. Функции нескольких переменных/ Под ред. В. Ф. Бутузова. – М.: Высш. шк., 1988. – 288 с.; 13. Мордкович А.Г., Солодовников А.С. Математический анализ.– М.: Вербум, 2001. – 416 с.; 14. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1,2. М.: Наука, 1985.; 15. Практикум по высшей математике для экономистов./Кремер Н.Ш., Тришин И.М., Путко Б.А. и др.; Под ред. проф. Н.Ш. Кремера.– М.: ЮНИТИ, 2005. – 479 с.; 16. Практикум по курсу математического анализа. Ч. 3. Интегральное исчисление для функций одной переменной / Н. Г. Ованесов, С.А. Казаров, Р. Л. Шапиро, Н. В. Трубицын. – Астрахань: Изд-во АГПИ, 1993. – 42 с.; 17. Сборник задач по математике для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. Т.1, 2. М.: Наука,1981.; 18. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. В 2-ч ч. Ч.2. – М.: Финансы и статистика, 2003.– 560с.; 19. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. – М.: Наука, 1966. – 606 с.; 20. Шипачев В. С. Задачник по высшей математике: Учеб. пособие для вузов. – М.: Высш. шк., 2001. – 304 с.; 21. Шипачев В.С. Математический анализ. – М.: Высшая школа, 2001. – 176 с. ПРИЛОЖЕНИЕ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
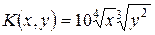 (
(  – количество единиц первого ресурса,
– количество единиц первого ресурса,  – второго). Стоимость единицы первого ресурса – 2, второго –
– второго). Стоимость единицы первого ресурса – 2, второго –  ден. ед. Найти максимальную прибыль при использовании ресурсов.
ден. ед. Найти максимальную прибыль при использовании ресурсов.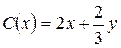 . Таким образом, функция прибыли равна
. Таким образом, функция прибыли равна
 равны
равны  ;
;  . Приравнивая их к нулю, найдем решение
. Приравнивая их к нулю, найдем решение  ,
,  . Частные производные второго порядка имеют вид:
. Частные производные второго порядка имеют вид:  ,
,  ,
,  .
. .
.  .
. (ден. ед.).
(ден. ед.).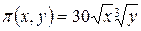 , стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600 ден. ед. В этих условиях найти оптимальное для производителя значение
, стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600 ден. ед. В этих условиях найти оптимальное для производителя значение  количества используемых ресурсов.
количества используемых ресурсов.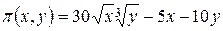 , при условии, что
, при условии, что  . Оптимальное распределение ресурсов в ситуации, когда ограничение отсутствует можно найти аналогично примеру 1
. Оптимальное распределение ресурсов в ситуации, когда ограничение отсутствует можно найти аналогично примеру 1 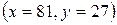 . Тогда оптимальные затраты на ресурсы равны
. Тогда оптимальные затраты на ресурсы равны 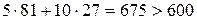 . Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму.
. Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму. , или
, или  .
. и
и  .
. . Приравнивая ее к нулю, получим решение
. Приравнивая ее к нулю, получим решение  , откуда
, откуда  . Максимальная прибыль при этом равна
. Максимальная прибыль при этом равна  (ден. ед.).
(ден. ед.). . Очевидно, что если какое-то значение
. Очевидно, что если какое-то значение  уровня функции
уровня функции  должна пересекаться с прямой
должна пересекаться с прямой  может быть записано как
может быть записано как  , где
, где  .
. , а, следовательно, и уровня
, а, следовательно, и уровня 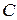 достигается в том случае, если соответствующая линия уровня касается прямой
достигается в том случае, если соответствующая линия уровня касается прямой  . Так как градиент в каждой точке ортогонален линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом: вектор
. Так как градиент в каждой точке ортогонален линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом: вектор 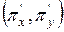 ортогонален прямой
ортогонален прямой  . Угловой коэффициент прямой, проходящей через вектор
. Угловой коэффициент прямой, проходящей через вектор  . По условию перпендикулярности прямых имеем
. По условию перпендикулярности прямых имеем  , т.е.
, т.е.  , или
, или  . Подставляя полученное выражение в управление прямой
. Подставляя полученное выражение в управление прямой  .
. .
. , т.е.
, т.е.  . Используя свойства логарифмов, имеем:
. Используя свойства логарифмов, имеем: , т.е.
, т.е. 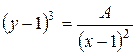 , где
, где  .
. .
. , или
, или  . Значит, градиент функции полезности должен быть перпендикулярен этой линии. Градиент функции полезности имеет вид
. Значит, градиент функции полезности должен быть перпендикулярен этой линии. Градиент функции полезности имеет вид 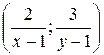 . Угловой коэффициент прямой
. Угловой коэффициент прямой  . Используя условие перпендикулярности прямых, имеем
. Используя условие перпендикулярности прямых, имеем 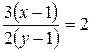 , или
, или  . Следовательно, оптимальное распределение потребления товаров находится как решение системы:
. Следовательно, оптимальное распределение потребления товаров находится как решение системы: т.е.
т.е.  .
.