
|
|
Первообразная функции и неопределенный интеграл.Вычислить неопределённый интеграл означает восстановить функцию по известной производной этой функции. Восстановленная таким образом функцияF(x) называется первообразной для функции f(x). Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции. Поставим задачу интегрирования: для данной функцииf(x)найти такую функциюF(x),производная которойравнаf(x). Пример. Для функции Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.
Следовательно, функция
где С – произвольная постоянная. В этом можно убедиться дифференцированием. Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции Теорема.Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная. Основные свойства неопределенного интеграла. Теорема 1.Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению. Теорема 2.Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями. Теорема 3.Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
Теорема 4.Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
Основные методы интегрирования: непосредственное, замена переменной, интегрирование по частям. Метод непосредственного интегрирования Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтег-ральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Задание. Найти интеграл Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к нескольким табличным.
Интегрирование заменой переменной Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся. Если в неопределенном интеграле
Эта формула называется формулой замены переменной в неопределенном интеграле. После нахождения интеграла по новой переменной В некоторых случаях целесообразно делать подстановку
Задание. Найти интеграл Решение. Сделаем замену переменной:
Ответ. Интегрирование по частям Рассмотрим функции
Проинтегрировав левую и правую части последнего равенства, получим:
Полученное равенство перепишем в виде:
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл В некоторых случаях формулу интегрирования частями нужно применять неоднократно. Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
Здесь Задание. Найти интеграл Решение. В исходном интеграле выделим функции
Ответ. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.
называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.
 этому условию удовлетворяет функция
этому условию удовлетворяет функция  так как
так как 
 или
или 
 - первообразная для функции
- первообразная для функции  . Однако она не является единственной первообразной для
. Однако она не является единственной первообразной для 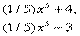 и вообще
и вообще 
 записываются в приведённом выше виде. Это вытекает из следующей теоремы.
записываются в приведённом выше виде. Это вытекает из следующей теоремы.

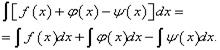






 сделать подстановку
сделать подстановку  , где функция
, где функция  - функция с непрерывной первой производной, то тогда
- функция с непрерывной первой производной, то тогда  и согласно свойству 6 неопределенного интеграла имеем, что:
и согласно свойству 6 неопределенного интеграла имеем, что:
 необходимо вернуться к первоначальной переменной
необходимо вернуться к первоначальной переменной  .
. , тогда
, тогда

 , далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.
, далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.
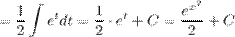

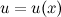 и
и  , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство: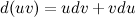


 можно свести к нахождению интеграла
можно свести к нахождению интеграла  , который может быть более простым.
, который может быть более простым. ;
;  ;
; 
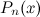 - многочлен степени
- многочлен степени  ,
,  - некоторая константа. В данном случае в качестве функции
- некоторая константа. В данном случае в качестве функции  берется многочлен, а в качестве
берется многочлен, а в качестве  - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется
- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 
 , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.


