
|
|
Свойства неопределенного интеграла1. 2. 3. 4. 5. Если
Таблица основных неопределенных интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
Интегралы от некоторых элементарных функций не являются элементарными функциями, например:
Основные методы интегрирования Непосредственное интегрирование Непосредственным интегрированием называется вычисление интегралов путем использования таблицы основных неопределенных интегралов, их свойств, а также тождественных преобразований подынтегрального выражения. Пример1. Найти Решение.
Пример2. Найти Решение. Воспользуемся свойством 5:
Пример3. Найти. Решение. Воспользуемся формулами тригонометрии:
Интегрирование путем подведения под знак дифференциала Все формулы таблицы основных интегралов справедливы, когда переменная интегрирования не является независимой, а представляет функцию от некоторой другой переменной: Тогда Пример 4. Вычислить интеграл Решение. Так как то Здесь мы применили формулу 1 таблицы интегралов. Пример 5. Вычислить интеграл Решение. Заметим, что
Замена переменой в неопределенном интеграле Замена переменной или метод подстановки, состоит в том что, при вычислении интеграла Введем новую переменную
Пример6. Вычислить интеграл Решение. Применим подстановку
Пример7. Вычислить интеграл Решение. Применяем подстановку
Интегрирование по частям в неопределенном интеграле Теорема. Если функции Эта формула называется формулой интегрирования по частям. Она позволяет свести вычисление интеграла Метод интегрирования по частям применяется при вычислении следующих интегралов: А) В) В этих интегралах за Пример 8. Вычислить Решение. Положим
Пример 9. Вычислить Решение. Положим Отсюда
Пример 10. Вычислить Решение. Примем
Пример11. Вычислить Решение. Сделаем предварительные преобразования:
Интегрирование рациональных дробей Рациональной дробью
где, m, n – целые положительные числа, Если Всякую неправильную дробь путем деления
где Интегрирование правильной рациональной дроби основано на следующей теории. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех видов:
где, A, a, M, N, p, q – действительные числа, k – натуральное число В алгебре устанавливается, что если знаменатель дроби представить в виде:
то в разложении самой дроби: а) каждому множителю вида б) каждому множителю вида
в) каждому множителю Пример12. Найти интеграл Решение. Разложим правильную рациональную дробь на сумму простейших дробей:
Приводя дроби к общему знаменателю и приравнивая числители, получим:
Так как данное тождество должно выполняться для любого Приравнивая коэффициенты при одинаковых степенях При При При При Подставив значение Поэтому:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



 ,
,  ,
, 
 первообразная для
первообразная для 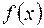 , тогда
, тогда ,
, 
 ;
; 





 ,
, 
 ,
,  ,
, 





 .
.

 .
. .
. .
. .
. .
. или
или  .
. .
. ,
, .
. .
. , тогда имеем:
, тогда имеем: .
. вместо переменной
вместо переменной  вводится новая переменная
вводится новая переменная  , связанная с
, связанная с  . При этом функцию
. При этом функцию  следует выбирать так, чтобы подынтегральная функция становилась более удобной для интегрирования.
следует выбирать так, чтобы подынтегральная функция становилась более удобной для интегрирования. .
. .
. , а затем продифференцируем это равенство:
, а затем продифференцируем это равенство: 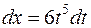 .
.
 =
=  .
. .
. , тогда
, тогда  .
. .
. и
и  дифференцируемы на интервале
дифференцируемы на интервале  , то
, то  .
. к вычислению интеграла
к вычислению интеграла  , который может оказаться более простым.
, который может оказаться более простым. ,
,  ,
,  , где
, где  - многочлен степени n. В этих интегралах за
- многочлен степени n. В этих интегралах за  ,
,  ,
,  ,
,  ,
,  .
. принимается
принимается  .
. .
. , тогда
, тогда  ,
, и по формуле интегрирования по частям получаем:
и по формуле интегрирования по частям получаем: .
. .
. .
. . Используя формулу интегрирования по частям, имеем:
. Используя формулу интегрирования по частям, имеем:
 .
. .
.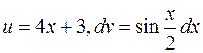 , тогда
, тогда 
 . Окончательно получаем:
. Окончательно получаем:
 .
. .
.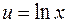 ,
, 

 отсюда
отсюда .
. называется функция, равная отношению двух многочленов:
называется функция, равная отношению двух многочленов: ,
, - действительные числа (
- действительные числа (  ).
). , то
, то  - неправильной дробью.
- неправильной дробью. на
на  можно представить в виде суммы некоторого многочлена и правильной дроби.
можно представить в виде суммы некоторого многочлена и правильной дроби. ,
,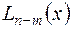 ,
,  - многочлены;
- многочлены; 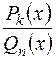 - правильная рациональная дробь
- правильная рациональная дробь 


 .
.

 ,
, соответствует одна простейшая дробь вида
соответствует одна простейшая дробь вида  ;
; соответствует сумма простейших дробей вида:
соответствует сумма простейших дробей вида: ;
; соответствует одна простейшая дробь вида
соответствует одна простейшая дробь вида  .
. .
. .
.
 и получим
и получим  .
. :
: 
 :
: 

 :
: 
 , находим:
, находим:  ,
,  ,
,  .
.