
|
|
Методические указания к выполнению контрольной работыМАТЕМАТИКА
Методические указания к изучению дисциплины и выполнению контрольной работы №2 для студентов I курса заочной формы обучения
Составители доктор физ.-мат. наук, профессор М.М. Галилеев канд. технических наук, доцент В.Н. Ассаул старший преподаватель П.С. Беломутская старший преподаватель Н.В. Кошкина
Рецензент
кандидат физ.-мат. наук, доцент А.М.Балонишников Подготовлено на кафедре высшей математики
Содержание 1. Общие положения 4 2. Методические указания к изучению дисциплины 5 3. Методические указания к выполнению контрольной работы 6 4. КОНТРОЛЬНАЯ РАБОТА №2 Контрольные задания 17 Указания к заданию 2. ТЕМА 2. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 19 Контрольные задания 24 Указания к заданию 3. ТЕМА 3. ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА 26 Контрольные задания 33 Указания к заданию 4. ТЕМА 4. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 34 Контрольные задания 36 Указания к заданию 5. ТЕМА 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 38 Контрольные задания 49 Указания к заданию 6. ТЕМА 6. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 51 Контрольные задания 58 5. Требования к выполнению контрольной работы 61 6. Список литературы 62 Приложение 1 63 Приложение 2 66 Общие положения Цель курса - дать необходимый математический аппарат и привить навыки его использования при решении инженерно-экономических задач. Для этого при изучении курса студенты осваивают методы математического моделирования экономических ситуаций, математические методы их исследования и решения, методы анализа полученных результатов. Это способствует также развитию логического и алгоритмического мышления. Значительная часть материала выносится на самостоятельную проработку, что служит развитию навыков самостоятельного изучения литературы по математике и ее приложениям. Математика как учебная дисциплина в системе обучения инженеров-экономистов опирается на школьный курс математики, используя все его разделы. Изученные в курсе математики методы и алгоритмы используются во всех параллельных и следующих за ним курсах дисциплин. Формой контроля является экзамен. 2. Методические указания к изучению дисциплины Рекомендуется изучение методического пособия в порядке изложения материала. Возможно изучение отдельной темы. В качестве дополнительной литературы рекомендуется использовать издания, указанные в списке литературы. В методических указаниях приведены краткие теоретические сведения по каждому типу задач с подробными пояснениями к их решению. Методические указания могут быть использованы студентами заочной формы обучения при выполнении контрольных работ, а также при подготовке к экзамену. Контрольная работа №2 включает задания по следующим темам: 1. Предел функции (2 задания); 2. Основы дифференциального исчисления (2 задания); 3. Исследование функции и построение графика (1 задание); 4. Функции двух переменных (1 задание); 5. Неопределенный интеграл (3 задания); 6. Определенный интеграл (3 задания). Целостное представление о содержании курса дает Приложение 1. Содержание дисциплины (извлечение из рабочей программы дисциплины), где показаны принципы и логика построения дисциплины. Необходимость выпуска настоящего пособия вызвана особенностями заочной формы обучения.
Методические указания к выполнению контрольной работы Выполнение контрольных работ служит решению задачи получения студентами необходимых практических навыков по решению заданий из курса математики. Выполнение контрольных работ нацелено на получение студентами необходимых практических навыков решения задач из курса математического анализа. Прежде чем приступить к их выполнению, необходимо внимательно изучить соответствующие разделы Методических указаний, попробовав самостоятельно решить разобранные примеры. В случае возникновения затруднений, а также при необходимости более глубокого изучения вопроса, следует обратиться к рекомендованной учебно-методической литературе. Процесс работы над контрольной работой является важным этапом подготовки к зачету. Номер выполняемой работы определяется путем деления шифра (номера зачетной книжки) на 20 и равен остатку, получающемуся при делении. Например, для зачетной книжки №1972 это вариант №12. 4. КОНТРОЛЬНАЯ РАБОТА №2 Указания к заданию 1. Областью определения функции Пусть функция
Число
Аналогично, число Например, для функции Можно доказать, что для существования предела функции Если для любого Если же для любого Важным частным случаем последнего определения является предел числовой последовательности. Если функция Отметим следующие свойства пределов:
1. Если 2. 3. 4. 5. Дадим несколько определений, важных для дальнейшего. Функция Для вычисления пределов важны следующие свойства бесконечно малых величин. Пусть 1. 2. 3. 4. Если существует 5. Для монотонно возрастающей функции ( Рассмотрим две бесконечно малые величины Рассмотрим несколько примеров. Пример1. Вычислить предел Решение.Очевидно, что числитель дроби Здесь мы использовали свойства пределов, о которых говорилось выше. Пример2. Вычислить предел Решение. Очевидно, Поскольку числитель в окрестности точки Пример3. Вычислить предел Решение. Если подставить Вернемся к примеру. Разложим числитель на множители:
Рассмотрим
Пусть
Нетрудно видеть, что при Если
Рассмотрим теперь случай
Таким образом,
Рассмотрим два предела: С помощью несложных оценок можно показать, что В силу важности этих пределов их называют замечательными пределами. Используя замечательные пределы, можно получить следующие результаты:
Поэтому можно утверждать, что при Пример 4. Вычислить предел:
Решение.
Очевидно, что все подкоренные выражения при
Пример 5. Вычислить предел Решение. Подставив в заданную функцию Следовательно,
Следовательно,
Пример 6. Вычислить предел Решение. Это неопределенность вида
Пример7. Вычислить предел Решение. В данном случае имеем дело с неопределенностью вида
Тогда
Так как при то
Поскольку
Пример 8. Найти предел Решение. При
так как Пример 9. Найти предел Решение. Неопределенность вида Далее, Поэтому Пример10. Найти предел Решение. Неопределенность вида
Здесь учтено, что Контрольные задания Найти следующие пределы.
1.1 а)
1.2. а)
1.3. а)
1.4. а)
1.5. а)
1.6. а)
1.7. а)
1.8. а)
1.9. а)
1.10. а)
1.11. а)
1.12. а)
1.13. а) 1.14. а) 1.15. а)
1.16. а)
1.17. а)
1.18. а)
1.19. а)
1.20. а)
Указания к заданию 2. Пусть на интервале
Нахождение производной называют дифференцированием функции. Функцию
Можно доказать, что для дифференцируемости функции необходимо и достаточно, чтобы существовала и была конечной ее производная, при этом Выражение Геометрически дифференциал Если производная существует для всех Для освоения техники дифференцирования, то есть нахождения производных, необходимо использовать правила дифференцирования и таблицу производных наиболее часто встречающихся функций. Основные правила дифференцирования 1. 2. 3. 4. 5. Производная сложной функции: если Приведем таблицу производных наиболее часто используемых функций: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Логарифмической производной функции Функция y(x) называется неявной, если зависимость между х и у выражена уравнением F(x,y)=0, неразрешенным относительно у. Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая у функцией от х, а затем полученное уравнение решить относительно производной Рассмотрим примеры вычисления производных. Пример 1. Найти производную функции Решение. Применяя правила 4,1 и таблицу производных, получим:
Пример 2. Найти Решение. Последовательно применяя правило дифференцирования сложной функции, получим:
Пример 3. Найти производную функции Решение. Применим логарифмическую производную:
Пример4. Найти производную функции Решение. В случае произведения нескольких сомножителей применение логарифмической производной также эффективно:
Пример 5. Найти производную функции Решение. Применим правило дифференцирования неявной функции:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называют те значения
называют те значения  , для которых данное выражение имеет смысл и значения
, для которых данное выражение имеет смысл и значения  конечны.
конечны. определена в некоторой окрестности точки
определена в некоторой окрестности точки 
 . Если для любого
. Если для любого  > 0 найдется такое число
> 0 найдется такое число  > 0, что при всех
> 0, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , будет выполнено неравенство
, будет выполнено неравенство , то число
, то число  называют пределом функции
называют пределом функции  в точке
в точке 
 называется левосторонним пределом функции
называется левосторонним пределом функции  , если для любого
, если для любого  , будет выполнено неравенство
, будет выполнено неравенство . Левосторонний предел обозначают следующим образом:
. Левосторонний предел обозначают следующим образом: 
 .
. называется правосторонним пределом функции
называется правосторонним пределом функции  следует
следует  и
и 
 .
. в точке
в точке  имеет смысл говорить только о левостороннем пределе, а для функции
имеет смысл говорить только о левостороннем пределе, а для функции  в точке
в точке  существует
существует 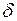 > 0, такое, что при всех
> 0, такое, что при всех  будет выполнено условие
будет выполнено условие  , то предел функции
, то предел функции  .
. существует
существует  , такое, что при всех
, такое, что при всех 

 .
. (
(  =
= 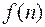 ), а ее предел
), а ее предел  ─ пределом последовательности
─ пределом последовательности 
 Таким образом, число
Таким образом, число  существует
существует  , такое, что при
, такое, что при  выполняется неравенство
выполняется неравенство  .
. существует, то он единственный.
существует, то он единственный. (
(  постоянное число);
постоянное число);

 (
(  ).
). . Функция
. Функция  . Функция
. Функция  , такое, что
, такое, что  при всех
при всех  и
и  ─ бесконечно малые, а
─ бесконечно малые, а  ─ бесконечно малая величина в окрестности точки
─ бесконечно малая величина в окрестности точки  ─ бесконечно малая величина в окрестности точки
─ бесконечно малая величина в окрестности точки  ─ бесконечно малая величина в окрестности точки
─ бесконечно малая величина в окрестности точки  , то это равносильно тому, что в окрестности точки
, то это равносильно тому, что в окрестности точки 
 , где
, где  ─ бесконечно малая величина в окрестности этой точки;
─ бесконечно малая величина в окрестности этой точки; при
при  ) или монотонно убывающей (
) или монотонно убывающей (  при
при  , то говорят, что
, то говорят, что  . Если
. Если  , то
, то  .
. при
при  стремится к
стремится к  . Аналогично знаменатель стремится к
. Аналогично знаменатель стремится к  . Тогда вся дробь будет стремиться к
. Тогда вся дробь будет стремиться к  . Таким образом,
. Таким образом,  .
. .
. , а
, а  при
при  . Таким образом, дробь будет стремиться к бесконечности, так как знаменатель ─ бесконечно малая величина, а обратная ей величина ─ бесконечно большая.
. Таким образом, дробь будет стремиться к бесконечности, так как знаменатель ─ бесконечно малая величина, а обратная ей величина ─ бесконечно большая. ограничен, получаем:
ограничен, получаем:  .
. .
. . Встречаются также неопределенности вида
. Встречаются также неопределенности вида  ,
,  ,
,  ,
,  , для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенности.
, для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенности. .
. , где
, где  и
и  ─ многочлены степени
─ многочлены степени 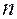 и
и  :
: 

 Разделим числитель и знаменатель почленно на
Разделим числитель и знаменатель почленно на 

 все слагаемые числителя, кроме последнего, стремятся к нулю, а в знаменателе все слагаемые стремятся к нулю. Таким образом,
все слагаемые числителя, кроме последнего, стремятся к нулю, а в знаменателе все слагаемые стремятся к нулю. Таким образом,  по аналогии с примером 2.
по аналогии с примером 2. , то
, то  , а дробь в знаменателе имеет уже степень числителя большую, чем степень знаменателя и, согласно только что рассмотренному случаю, стремится к бесконечности. Тогда имеем:
, а дробь в знаменателе имеет уже степень числителя большую, чем степень знаменателя и, согласно только что рассмотренному случаю, стремится к бесконечности. Тогда имеем: так как величина, обратная бесконечно большой, есть бесконечно малая величина.
так как величина, обратная бесконечно большой, есть бесконечно малая величина. Поделив числитель и знаменатель почленно на
Поделив числитель и знаменатель почленно на  , получим:
, получим:

 и
и  .
. Вычисление второго предела требует бóльших усилий, но можно доказать, что он равен числу
Вычисление второго предела требует бóльших усилий, но можно доказать, что он равен числу  (основанию натурального логарифма):
(основанию натурального логарифма):  . Доказательства можно найти в учебниках по математическому анализу.
. Доказательства можно найти в учебниках по математическому анализу. ;
;  ;
;  ;
; ;
;  .
.
 ~
~  ~
~  ~
~  ,
,  ~
~  ~
~ 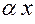 , где знак ~ означает эквивалентность соответствующих бесконечно малых величин. При вычислении пределов можно использовать эти соотношения эквивалентности, заменяя, например, отношения бесконечно малых на отношения эквивалентных им бесконечно малых величин.
, где знак ~ означает эквивалентность соответствующих бесконечно малых величин. При вычислении пределов можно использовать эти соотношения эквивалентности, заменяя, например, отношения бесконечно малых на отношения эквивалентных им бесконечно малых величин. .
.



 стремятся к единице, а вторые слагаемые в скобках ─ к нулю. Поэтому последний предел равен следующему:
стремятся к единице, а вторые слагаемые в скобках ─ к нулю. Поэтому последний предел равен следующему:
 .
. . Известно, что если
. Известно, что если  , где
, где  ─ многочлен степени
─ многочлен степени  .
. . Проще всего узнать вид многочлена
. Проще всего узнать вид многочлена  , разделив
, разделив  на
на  . Это можно сделать, выполнив деление «столбиком», как делят числа:
. Это можно сделать, выполнив деление «столбиком», как делят числа:












 . Тогда, разлагая на множители разность кубов в знаменателе, получим:
. Тогда, разлагая на множители разность кубов в знаменателе, получим:
 .
. :
:
 .
.

 ─ бесконечно малая величина,
─ бесконечно малая величина,
 , получаем:
, получаем:

 рассматриваемая функция имеет неопределенность вида
рассматриваемая функция имеет неопределенность вида  . Когда переменная
. Когда переменная  , переменная
, переменная  . Тогда рассматриваемый предел принимает вид:
. Тогда рассматриваемый предел принимает вид:
 ~
~  , а
, а  .
.

 ~
~  . Поэтому
. Поэтому  ~
~  .
. ~
~  .
.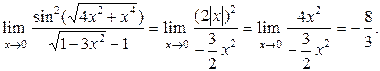
 .
. Тогда получим:
Тогда получим:
 ~
~  при
при  б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 задана функция
задана функция  и придадим аргументу
и придадим аргументу  . Тогда значение функции получит приращение
. Тогда значение функции получит приращение  . Рассмотрим отношение
. Рассмотрим отношение 
 . Если при
. Если при 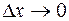 существует конечный предел дроби
существует конечный предел дроби  (или
(или  ):
): .
. .
. .
. называют дифференциалом функции и обозначают
называют дифференциалом функции и обозначают  . Приращение аргумента
. Приращение аргумента  называют дифференциалом независимой переменной и обозначают
называют дифференциалом независимой переменной и обозначают  . Таким образом,
. Таким образом,  .
. есть приращение касательной, проведенной к графику функции в точке
есть приращение касательной, проведенной к графику функции в точке  . Для линейной функции
. Для линейной функции 

 Аналогично вводится понятие высших производных (производные, начиная со второй, называются производными высшего порядка).
Аналогично вводится понятие высших производных (производные, начиная со второй, называются производными высшего порядка).
 .
. (
(  – постоянная)
– постоянная)  .
.


 .
. , то
, то  , где производные функций в правой части равенства берутся по аргументам
, где производные функций в правой части равенства берутся по аргументам  и
и  (
( 
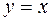



 (
( 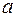 – постоянная)
– постоянная) 






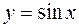















 , при y > 0. Нахождение производных от многих функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0.
, при y > 0. Нахождение производных от многих функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0. .
. .
.

 .
. , если
, если  .
.
 .
.
 .
.

 .
. , если
, если  .
.



