
|
|
МАТЕМАТИЧЕМКАЯ СТАТИСТИКАМатематическая статистика Программные вопросы 1. Генеральная и выборочная совокупности и их объёмы. 2. Вариационный и интервальный ряды распределения. Статистическое распределение. Полигон и гистограмма. 3. Основные характеристики вариационного ряда: выборочная средняя, низшая и высшая средние, мода и медиана, выборочная дисперсия и среднее квадратическое отклонение; исправленная дисперсия, стандарт, коэффициент вариации. 4. Статистическая гипотеза. Проверка гипотезы о нормальном распределении признака с помощью критериев согласия 5. Точечные и интервальные оценки генеральной средней и генерального среднего квадратического отклонения для нормально распределённого признака. 6. Ошибки выборочных оценок.
Решение типового примера
Пример 13.1.В таблице 1 приведены денежные затраты Х на животноводство, заданные выборкой по 60 хозяйствам области, дес. тыс. руб. на 100 голов. Требуется для признака Х: 1. Построить интервальный ряд распределения; для каждого интервала подсчитать локальные, а также накопленные частоты; построить вариационный ряд; 2. Построить полигон и гистограмму; 3. Определить выборочную среднюю; а также низшую и высшую частные средние; моду и медиану; дисперсию и среднее квадратическое отклонение; коэффициент вариации; 4. Проверить при уровне значимости 0,05 гипотезу о нормальном законе распределения соответствующего признака с помощью критериев согласия χ2 ─ Пирсона и 5. Найти точечные и интервальные оценки генеральной средней и среднего квадратического отклонения (при доверительной вероятности р = =0,95); 6. Найти ошибки выборочных оценок; 7. Произвести анализ всех вычисленных статистических параметров. Таблица 13.1 Распределение затрат на животноводство
Решение. 1) Составим интервальный ряд для признака Х. Для этого найдём размах варьирования значений признака по формуле: RХ =Xmax - Xmin. Из таблицы 13.1 следует: Xmax = 68 ; Xmin = 18 и RХ = 68 - 18 = 50. Число интервалов m, на которые следует разбить интервал значений признака, найдём по формуле Стерджеса: m = 1+3,322 lg n, где n - объём выборки, то есть число единиц наблюдения. В нашем примере n=60. Получим: m = 1+3,322•lg 60 = 1+3,322•1,778 = =6,9 ≈7.
Теперь рассчитаем шаг (длину частичного интервала) h по формуле: h= За начало первого интервала принимаем такое значение из интервала [хmin- Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал.
Его вершины, стороны и диагонали обозначают одну единицу. Итого: 4 вершины, 4 стороны и 2 диагонали. Всего 10 единиц. Например, 2; -7; - 8; - 10. Таблица 13.2 Распределение частот денежных затрат на животноводство
В табл. 13.2 произведена разноска значений признака Х, указаны интервалы, середины интервалов, частоты ni, накопленные частоты, равные сумме частот, попавших в предшествующие интервалы. Интервалы и их частоты представляют собой интервальный ряд. Середины интервалов и соответствующие частоты дают вариационный ряд (табл. 13.3). Таблица 13.3 Вариационный ряд
2) Графически интервальный ряд изображают с помощью гистограммы. Для её построения в прямоугольной системе координат на оси абсцисс откладывают отрезки, соответствующие интервалам вариационного ряда. На этих отрезках строят прямоугольники с высотами, равными частотам. Полученная ступенчатая фигура, состоящая из прямоугольников, и есть гистограмма. Для признака Х гистограмма изображена на рис. 13.1.
n Рис. 13.1. Гистограмма распределения денежных затрат на животноводство
Для графического изображения дискретного ряда служит многоугольник (полигон). Для его построения на оси абсцисс откладываются варианты, а на оси ординат их частоты. Полученные точки соединяют отрезками. Полигон вариационного ряда признака Х изображён
на рис.13 2.
Рис. 13.2. Полигон денежных затрат на животноводство
3) Для интервального ряда распределения выборочная средняя вычисляется по формуле:
где хi - середина i - го интервала, ni - частота i- го интервала, n – объём выборки. Используя данные табл. 13.3., вычислим средние затраты на животноводство: Низшая и высшая частные средние находятся по формулам:
причём в знаменателе суммируются частоты тех же групп, что и в числителе. Вычисляем:
Для характеристики рядов распределения применяют также структурные средние: моду Мо и медиану Ме. Мода – это варианта, которая наиболее часто встречается в данной совокупности, то есть варианта с наибольшей частотой. Для интервального ряда (с равными интервалами) мода определяется по следующей формуле:
где h - шаг, В нашем случае Мо=40+ Медианой в статистике называют варианту, расположенную в середине вариационного ряда. Для интервального ряда медиану определяют по формуле:
где хМе - начало медианного интервала (содержащего медиану), nн Me-1 - накопленная частота интервала, предшествующего медианному, nМе - локальная частота медианного интервала. В нашем примере, используя данные таблицы 13.2, получим: Ме=40 +8 Дисперсия вариационного ряда служит для характеристики рассеяния значений признака вокруг среднего значения и вычисляется по формуле:
Для удобства вычислений дисперсии признака Х составим рабочую таблицу (см. табл. 13.4). Таблица 3.4
Таким образом, Среднее квадратическое отклонение (стандарт) SX - это арифметическое значение квадратного корня из дисперсии.
Таблица 3.5
Для сравнения величин рассеяния вариационных рядов вычисляют коэффициент вариации Vх как процентное отношение стандарта к средней арифметической: Для признака Х: Результаты вычислений поместим в табл. 13.5.
4) Проверим гипотезу о соответствии данных ряда (табл. 3.3) нормальному закону распределения сначала по критерию Пирсона χ2. Для этого сравним наблюдаемые ni и теоретические nit (вычисленные в предположении нормального распределения) частоты. Теоретические частоты рассчитываются по формуле: Таблица13. 6
 5). Если частота группы ряда менее 5, то эту группу следует объединить с соседней. Расчёты проверки критерия Пирсона поместим в табл. 6, вычислив предварительно 5). Если частота группы ряда менее 5, то эту группу следует объединить с соседней. Расчёты проверки критерия Пирсона поместим в табл. 6, вычислив предварительно  , и используя, что , и используя, что  . .
Поскольку частоты крайних групп n1 = 3 < 5 и n7 = 3 < 5, то объединяем их с соседними группами. Сумма последнего столбца определяет фактическую величину критерия Пирсона χф2 = 0,94. Эта величина сравнивается с предельным значением χкр2, значения которой даны в таблице (приложение 4) в зависимости от уровня значимости В условиях задачи, принимая надёжность результатов равной 95%(р=0,95), уровень значимости расчётов будет равен Число групп вариационного ряда, после объединения первой и второй, а так же шестой и седьмой групп, равна
Сравнение фактического и критического значений даёт: Следовательно, с надёжностью р=95% можно принять гипотезу, что разность частот между фактическим и нормальным распределением несущественна, а получена за счёт случайных отклонений, и данное распределение вариант можно считать подчиняющимся закону нормального распределения. Критерий Пирсона, как правило, используется, когда объём выборки n>100. Когда же 50<n<100, то наиболее эффективен критерий Критерий Фактическое значение критерия Fit ─ теоретическое значение накопленной частости i-ой группы. Вычисленное значение Таблица 13.7
Для n = 60 Расчёт Сравнение фактического 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ─ Пирсона и
─ Пирсона и 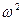 ─ Смирнова.
─ Смирнова. =
=  7,1. Округление шага производится, как правило, в большую сторону. Таким образом, принимаем h=8.
7,1. Округление шага производится, как правило, в большую сторону. Таким образом, принимаем h=8. ; хmin), чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём хmin - 2 = 18 - 2 = 16. В результате получим следующие границы интервалов: 16-24-32-40-48-56-64-72.
; хmin), чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём хmin - 2 = 18 - 2 = 16. В результате получим следующие границы интервалов: 16-24-32-40-48-56-64-72.





 Для удобства подсчёта частот используют «метод конверта»:
Для удобства подсчёта частот используют «метод конверта»:








 15
15 11
11 9
9
 5
5 3
3 0 20 28 36 44 52 60 68 xi
0 20 28 36 44 52 60 68 xi
 ,
, =
=  , то есть 455 тыс. руб. на 100 голов.
, то есть 455 тыс. руб. на 100 голов. и
и  ,
, ;
; .
. ,
, - частота модального (содержащего моду) интервала;
- частота модального (содержащего моду) интервала;  - частота домодального интервала;
- частота домодального интервала;  - частота послемодального интервала;
- частота послемодального интервала;  - начало модального интервала.
- начало модального интервала. =46,4.
=46,4.
 ≈45,9
≈45,9 .
.
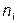



 .
. .
.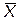


 .
. .
. , где nit ─ теоретические частоты, n ─ объём выборки, h ─ шаг (длина) частичного интервала,
, где nit ─ теоретические частоты, n ─ объём выборки, h ─ шаг (длина) частичного интервала,  ─ нормированное отклонение, xi ─ середины частичных интервалов,
─ нормированное отклонение, xi ─ середины частичных интервалов,  ─ выборочная средняя, SХ ─ стандарт,
─ выборочная средняя, SХ ─ стандарт,  ─ дифференциальная функция Лапласа (значения даны в приложении 1).
─ дифференциальная функция Лапласа (значения даны в приложении 1).

 и числа степеней свободы
и числа степеней свободы  , где
, где  ─ число групп вариационного ряда.
─ число групп вариационного ряда. .
. и к=2, находим по таблице приложения 4.
и к=2, находим по таблице приложения 4.
 .
. ф2 вычисляют по формуле:
ф2 вычисляют по формуле:  , где Fi ─ накопленная частость i-ой группы,
, где Fi ─ накопленная частость i-ой группы, сравнивают с критическим значением
сравнивают с критическим значением  , которое находится по таблице для величины n и уровня значимости
, которое находится по таблице для величины n и уровня значимости  .
.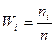

 .
.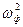 и предельного
и предельного 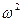 даёт:
даёт:  Следовательно, с надёжностью р = 0,95. можно полагать, что данная выборка подчиняется закону нормального распределения.
Следовательно, с надёжностью р = 0,95. можно полагать, что данная выборка подчиняется закону нормального распределения.