
|
|
Задачи контрольной работыВ заданиях 5.1.1 -5.1.20 продифференцировать указанные функции, пользуясь правилами и формулами дифференцирования.
ИССЛЕДОВАНИЕ ФУНКЦИЙ Программные вопросы 1. Область определения функции. 2. Исследование функции на четность, нечетность и периодичность. 3. Нахождение участков непрерывности функции и точки разрыва с указанием вида разрыва. 4. Точки пересечения с осями координат. 5. Асимптоты графика функции. 6. Интервалы возрастания и убывания функции. 7. Экстремумы функции. 8. Интервалы выпуклости и вогнутости и точки перегиба функции. Решение типового примера Пример 1.1. Исследовать заданную функцию Исследование функций и построение графиков рекомендуется проводить по следующей схеме: 1) найти область определения функции D(y) и исследовать функцию на непрерывность, найти точки разрыва функции, ее односторонние пределы в точках разрыва; 2) проверить четность (нечетность) функции; 3) найти точки экстремума функции и определить интервалы ее монотонности; 4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика; 5) найти наклонные асимптоты графика функции; 6) построить график, используя результаты предыдущих исследований. Решение. 1)Областью определения данной функции являются все действительные значения аргумента x, то есть 2) Исследуем функцию на четность (нечетность), для чего рассмотрим
Таким образом, мы видим, что
Таким образом, мы видим, что 3) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем ее к нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки x1 = – 5, x2 = – 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
4) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку
Значение 5) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты
Имеем
Таким образом, у графика заданной функции наклонных асимптот нет. 6) Для построения графика в выбранной системе координат изобразим точки максимума
Задачи контрольной работы
В примерах с 6.1.1-6.1.20 исследовать заданные функции методами дифференциального исчисления, начертить их графики.
Решение типового примера Пример 6.2. Исследовать заданную функцию Исследование функций и построение графиков рекомендуется проводить по следующей схеме:
1) найти область определения функции D(y) 2) исследовать функцию на непрерывность, найти точки разрыва функции, ее односторонние пределы в точках разрыва; 3) найти точки экстремума функции и определить интервалы ее монотонности; 4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика; 5) найти наклонные асимптоты графика функции; 6) построить график, используя результаты предыдущих исследований. Решение. 1) Область определения.
2) Исследование на непрерывность и классификация точек разрыва. Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика. 3) Исследование на экстремум и промежутки монотонности.
х1 = – 2, х2 = 10.
4) Исследование графика на выпуклость, вогнутость, точки перегиба.
Так как
5) Исследование графика на наличие наклонных асимптот.
Таким образом, прямая 6) Построение графика. Очевидно, график заданной функции пересекает ось Оу в точке (0; –5) и на основе обобщения результатов всех предыдущих исследований имеет вид, представленный на рис. 2.
Рис. 2

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  , д)
, д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в) 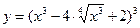 ,
д)
,
д)  .
.
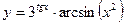 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 ,
в)
,
в)  ,
д)
,
д)  .
.
 ,
г)
,
г)  ,
,
 методами дифференциального исчисления, начертить ее график.
методами дифференциального исчисления, начертить ее график. , а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
, а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот. :
: .
. . Следовательно, функция не является четной.
. Следовательно, функция не является четной. .
. . Следовательно, функция не является нечетной. Поэтому, делаем вывод, что график функции - общего вида.
. Следовательно, функция не является нечетной. Поэтому, делаем вывод, что график функции - общего вида. ,
, 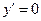
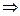
 ,
,  .
.






 ,
, .
. ,
, 

 .
.




 .
. воспользуемся формулами
воспользуемся формулами ,
,  .
. .
. , минимума
, минимума  , перегиба
, перегиба  . С учетом результатов предыдущих исследований построим кривую.
. С учетом результатов предыдущих исследований построим кривую.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.










 , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:



 – наклонная асимптота графика.
– наклонная асимптота графика.