
|
|
Задачи контрольной работыВ заданиях 4.2.1 – 4.2.20 найти указанные пределы.
Пример 4.3.Вычислить, используя первый замечательный предел:
Решение. При непосредственной подстановке получаем неопределенность:
В данном случае для освобождения от неопределенности будем использовать первый замечательный предел
Таким образом, нам не удалось избавиться от неопределенности. Воспользуемся формулами тригонометрии
Задачи контрольной работы В заданиях 4.3.1 – 4.3.20 найти указанные пределы, используя первый замечательный предел.
Пример 4.4.Вычислить, используя второй замечательный предел: а) Решение. а) При непосредственной подстановке получаем неопределенность:
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел
Т.о. наш предел примет вид:
Введем такую новую переменную
Таким образом, пользуясь свойствами пределов и правилами действия со степенями, будем иметь:
б) При непосредственной подстановке получаем неопределенность:
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел Выразив основание и показатель степени через
в) При непосредственной подстановке получаем неопределенность:
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел
Задачи контрольной работы В заданиях 4.4.1 – 4.4.20 найти указанные пределы, используя второй замечательный предел.
Производные Программные вопросы 1. Сформулируйте определение производной. 2. Каков геометрический смысл производной? 3. Что называется касательной к кривой? Напишите уравнение касательной к графику функции y = f(x). 4. Каков механический смысл первой и второй производной? 5. Каковы правила вычисления производных от суммы, произведения, частного двух функций? 6. Сформулируйте правило вычисления производной сложной функции. Решение типового примера
Пример 5.Продифференцируйте указанные функции, пользуясь правилами и формулами дифференцирования. a) в) РЕШЕНИЕ. а) Это сложная логарифмическая функция, которая дифференцируется по формуле:
Окончательно получаем:
При решении использовали формулы дифференцирования:
б) Данная функция представляет собой произведение сложной показательной функции
Для того, чтобы закончить дифференцирование воспользуемся формулами дифференцирования сложной обратнотригонометрической и тригонометрической функций:
в) Это сложная степенная функция, которая дифференцируется по формуле:
При решении использовали формулы дифференцирования:
г) Данная функция представляет собой частное сложной обратнотригонометрической функции и разности сложной показательной и степенной функций. Воспользуемся правилом дифференцирования частного
д) Это показательно – степенная функция, которую можно продифференцировать, используя формулу
но эта формула сложна для запоминания, поэтому мы поступим иначе: 1. прологарифмируем обе части равенства и воспользуемся свойствами логарифмической функции
2. продифференцируем обе части равенства, считая
Или
3. Из полученного равенства выразим

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.
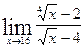 .
.
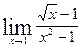 .
.
 .
.
 .
.
 .
.
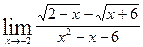 .
.
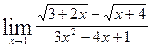 .
.
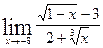 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
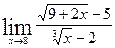 .
.
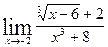 .
.
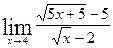 .
.
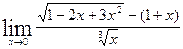 .
.
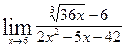 .
.
 .
. .
.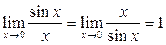 . Для этого сначала домножим числитель и знаменатель дроби под знаком предела на
. Для этого сначала домножим числитель и знаменатель дроби под знаком предела на 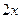 и воспользуемся свойствами пределов (предел произведения равен произведению пределов, если эти пределы существуют):
и воспользуемся свойствами пределов (предел произведения равен произведению пределов, если эти пределы существуют):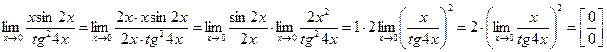 .
. и еще раз применим первый замечательный предел и свойства пределов:
и еще раз применим первый замечательный предел и свойства пределов: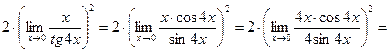
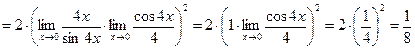 .
.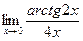 .
.
 .
.
 .
.
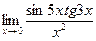 .
.
 .
.
 .
.
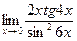 .
.
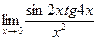 .
.
 .
.
 .
.
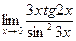 .
.
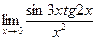 .
.
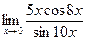 .
.
 .
.
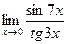 .
.
 .
.
 .
.
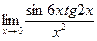 .
.
 ; б)
; б)  ; в)
; в) 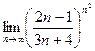 .
. .
. .
.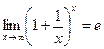 . Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины:
. Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины: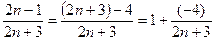 .
. .
. , что
, что 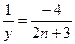
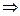
 ,
,  или
или  . При
. При  переменная
переменная 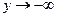 . Показатель степени примет вид:
. Показатель степени примет вид: .
.

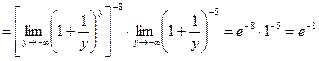 .
. .
.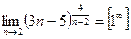 .
. . Для этого положим
. Для этого положим 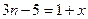 , или
, или  ,
, 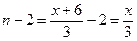 , тогда показатель степени примет вид:
, тогда показатель степени примет вид:  . При
. При 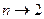 ,
,  .
. , а также воспользовавшись свойствами пределов и правилами действия со степенями, получим
, а также воспользовавшись свойствами пределов и правилами действия со степенями, получим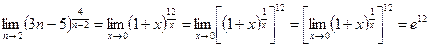 .
. .
.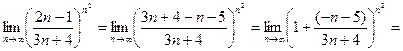
 .
. .
.
 .
.
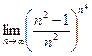 .
.
 .
.
 .
.
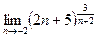 .
.
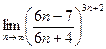 .
.
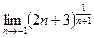 .
.
 .
.
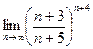 .
.
 .
.
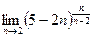 .
.
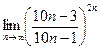 .
.
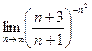 .
.
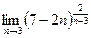 .
.
 .
.
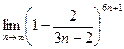 .
.

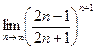 .
.
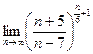 .
.
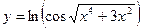 , b)
, b) 
 , г)
, г)  , д)
, д) 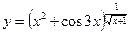 .
. .
.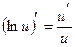 .
.
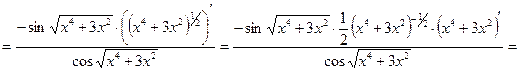
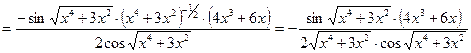 .
.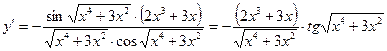 .
.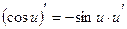 ,
,  .
. и сложной степенной функции
и сложной степенной функции  . Воспользуемся правилом дифференцирования произведения функций:
. Воспользуемся правилом дифференцирования произведения функций: 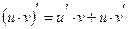 , а также формулами дифференцирования показательной и степенной функции:
, а также формулами дифференцирования показательной и степенной функции: ,
, 

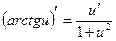 ,
,  .
.
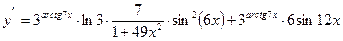 .
. .
. .
.
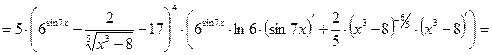
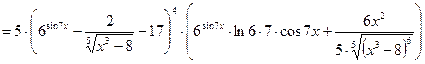 .
. ,
,  ,
,  .
. , а также формулами дифференцирования:
, а также формулами дифференцирования: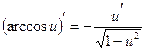 ,
,  ,
,  .
.
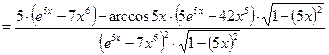 .
. .
.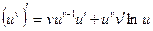 ,
,
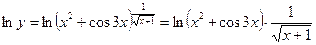 .
.
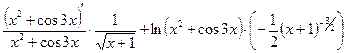 ,
,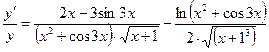 .
.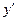
 .
.