
|
|
Расстояние от точки до прямой.
Расстояние d от точки
Пример: В треугольнике (рис.) с вершинами О(0,0), А(12,5) и В (6,8) найти уравнение сторон, высоты (В, К) биссектрисы (О, Е) угол
Решение: Используя (5), получим
Так как (В, К) Отсюда получаем (В, К) у – 8 = Отсюда, опять используя уравнения прямой проходящей через две точки, получаем уравнение (О, Е) : 7х – 9у = 0. По последней формуле для угла между прямыми - θ =
Наконец длину высоты найдем используя формулу расстояния точки В до прямой (О, А) :
Уравнения плоскости в пространстве.
Плоскость (Р), вложенную в д.с.к. пространства (рис. 14), вполне определяют лежащая на ней фиксированная точка М0 (х0,у0,z0) и любой ее так называемый нормальный вектор 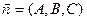 , перпендикулярный (Р). Условием принадлежности текущей точки М (х,у,z) (рис. 14) этой плоскости (Р) является равенство переписанное в виде , перпендикулярный (Р). Условием принадлежности текущей точки М (х,у,z) (рис. 14) этой плоскости (Р) является равенство переписанное в виде
(1, а)
или (1,б) оно именуется как векторное уравнение плоскости. Расписав в координатной форме (1,а) и (1,б) последовательно, получим: уравнение плоскости с нормальным вектором
; (2) и общее уравнение плоскости –
: (3)
Расстояние от точки до плоскости.
Расстояние d от точки М* (х*,у*,z*) до плоскости (рисунок ниже), заданной общим уравнением
может быть найдено по формуле
Пример: Найти: уравнение плоскости (Р0) (рис), содержащей точки А (1,1,1); Е(5,-1,1) и С(5,0,0); расстояние от D(6,2,2) до этой плоскости и уравнение плоскости (Р1), которая параллельна (Р0) и содержит точку D.
Решение: Возьмем сначала Сжав его в два раза получим (Р0): (х-1)+2(у-1)+2(z-1) = 0 или х+2у+2z –5=0 (Р1) : (х-6)+2(у-2)+2(z-2) = 0 или х+2у+2z-14=0 Теперь по формуле для расстояния от точки до плоскости расстояние D до (Р0):
Уравнение прямой в пространстве.
Прямую (l), вложенную в д.с.к. пространства (рис. 17), как и в плоскости вполне определяют лежащая на ней точка М0 (х0,у0,z0) и ее направляющий вектор
и здесь определяющего условие принадлежности к этой прямой её «текущей точки» М (х,у,z) получим векторное уравнение прямой
и далее параметрические уравнения прямой –
Канонические уравнения прямой
уравнение прямой, проходящей через две точки М0 (х0,у0,z0) и М1 (х1,у1,z1) –
Однако можно подойти к определению прямой в пространстве совсем по другому и задать её как пересечение любых двух пересекающихся по ней плоскостей, то есть системой
Расстояние от точки до прямой
Расстояние d от точки М* (х*,у*,z*) до прямой (l), направляющим вектором
Пример: Написать уравнение прямой, проходящей через точки А (1,1,5) и В (3,2,7) и найти расстояние от точки С (1,0,15) до этой прямой. Решение: Используя уравнение прямой проходящей через две точки, получаем
Последнее - уже каноническое уравнение прямой. Теперь по последней формуле находим:
Замечания о взаимном расположении. Так как ориентацию прямых и плоскостей в пространстве вполне определяют соответствующие направляющие или нормальные векторы, то их взаимное расположение (параллельность, перпендикулярность и пр.) характеризуется с помощью этих векторов. В частности, для нахождения угла φ между плоскостями с известными нормальными векторами
а для нахождения угла α между плоскостью с нормальным вектором
Пример: Будут ли плоскости 2х+3у-z+2=0 и 3х-у+9z-5=0 параллельны или перпендикулярны?
Решение:
Кривые второго порядка.
Назовем кривой второго порядка множество точек «координированной» плоскости, координаты х и у которых удовлетворяют так называемому общему уравнению кривых второго порядка Ах2 + Вху + Су2 + Dх + Еу + F = 0 Известно, что сменой системы координат - ее параллельным переносом (*) или (и) поворотом (**) когда координаты любой точки М ( (х', у') – «новые», а (х, у) – «старые») связываются формулами
 ; (*) ; (*)
или
это общее уравнение может быть преобразовано к одному из следующих так называемых «канонических» («образцовых») видов:
Из них, очевидно, (7) определяет пару параллельных прямых; (6) - пару пересекающих прямых; (5) - точку (0,0) и (4) и (8) - «ничего» не определяют. Наконец, будем называть: эллипсом кривую, которая в некоторой д.с.к. определяется уравнением (1); гиперболой - кривую, которая в некоторой д.с.к. определяется уравнением (2) и параболой - кривую, которая в некоторой д.с.к. определяется уравнением (3). (За некоторую похожесть уравнений (8) и (4) на уравнения (7) и (1) их называют соответственно уравнениями пары мнимых параллельных прямых и уравнением мнимого эллипса). Итак, повторим ещё раз что
В первом случае а и в, (а>в) называют, соответственно, большой и малой полуосями, а число Во втором случае а и в называют соответственно действительной и мнимой полуосями, а фокусным расстоянием обзывают величину Точки F1 (-с, 0) и F2 (с, 0) в том и другом случае называют фокусами, величину Важнейшими характеристиками гиперболы и только гиперболы являются так называемые асимптоты. Это прямые Для параболы величины р именуется фокальным (не путать с фекальным) параметром, точка Каждая из этих трех кривых обладает так называемым общими свойством:
Обозначив через r1 и r2 расстояния от произвольной точки эллипса или гиперболы до фокусов F1 и F2 сформулируем их так называемые характеристические свойства r1 + r2 = 2 · а - для эллипса r1 - r2 = 2 · а - для гиперболы. Приведение к каноническому виду иллюстрируют следующие Примеры: 1. х2 + 4у2 + 4х – 24у = 0 Выделяя полный квадрат «при х и у» получаем (х+2)2 + 4 · (у-3)2 = 40. Поделив на 40, одновременно - полагая, х+2 = х'; у-3 = у', то есть перенося центр системы координат в точку О (-2,3), получаем
 каноническое уравнение эллипса. Здесь каноническое уравнение эллипса. Здесь 
Аналогично для уравнения 2. 3х2 – у2 + 12х – 2у = 0 получаем 3 · (х-2)2 – (у+1)2 = 12 – 1; х – 2 = х'; у + 1 = у'; О'(2, - 1),
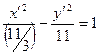 - каноническое уравнение гиперболы. - каноническое уравнение гиперболы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
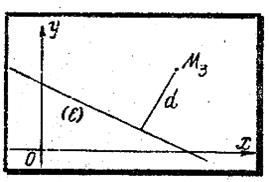
 до прямой (см. рис.), заданной общим уравнением
до прямой (см. рис.), заданной общим уравнением  может быть найдено по формуле
может быть найдено по формуле
 , длину (В, К)
, длину (В, К)
 или
или  ;
; или
или  ;
;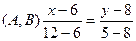 или
или  ;
; (А, О), то (24,3)
(А, О), то (24,3)  .
. или 12х + 5у – 112 = 0. Для нахождения уравнения (О ,Е) найдем координаты точки Е, используя то, что Е (конец биссектрисы) делит отрезок ВА в отношении
или 12х + 5у – 112 = 0. Для нахождения уравнения (О ,Е) найдем координаты точки Е, используя то, что Е (конец биссектрисы) делит отрезок ВА в отношении  . Так как длины |ОВ| = 10; |ОА| = 13, то
. Так как длины |ОВ| = 10; |ОА| = 13, то 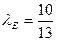 и по формуле деления отрезка в данном отношении получаем
и по формуле деления отрезка в данном отношении получаем  .
. - имеем
- имеем
 .
.






 . Отсюда используя соответствующее уравнение плоскости получаем
. Отсюда используя соответствующее уравнение плоскости получаем /
/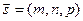 . Из равенства
. Из равенства


 ;
;


 - общие уравнения прямой.
- общие уравнения прямой. и
и  параллелограмма с площадью, равной |
параллелограмма с площадью, равной | 

 или
или 

 и
и  можно использовать формулу
можно использовать формулу ;
; и прямой с направляющим вектором
и прямой с направляющим вектором 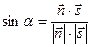 .
. и
и 


 . (**)
. (**)
 ; (1)
; (1)  ; (2)
; (2) ; (3)
; (3)  ; (4)
; (4)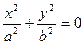 ; (5)
; (5)  ; (6)
; (6) ; (7)
; (7)  . (8)
. (8)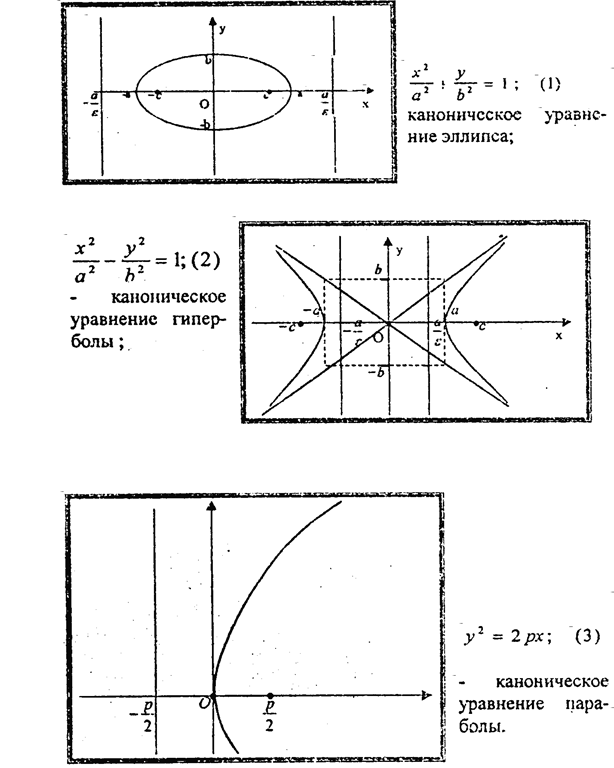
 - фокусным расстоянием.
- фокусным расстоянием. .
. - эксцентриситетом, а прямые
- эксцентриситетом, а прямые  и
и  - директрисами соответствующих эллипсов или гиперболы.
- директрисами соответствующих эллипсов или гиперболы. к которым сколь угодно близко приближаются точки гиперболы при неограниченном удалении их от начала координат.
к которым сколь угодно близко приближаются точки гиперболы при неограниченном удалении их от начала координат. - фокусом, а прямая (d): 2 · х + р = 0 - директрисой параболы. При этом считается, что эксцентриситет всех парабол равен 1. Легко заметить, что величина р выражает расстояние от фокуса F до директрисы (d). Отметим, что точка О (0,0) принадлежит канонической параболе и называется ее вершиной.
- фокусом, а прямая (d): 2 · х + р = 0 - директрисой параболы. При этом считается, что эксцентриситет всех парабол равен 1. Легко заметить, что величина р выражает расстояние от фокуса F до директрисы (d). Отметим, что точка О (0,0) принадлежит канонической параболе и называется ее вершиной.
