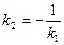|
|
Проекция вектора на вектор или осьПроекцией вектора
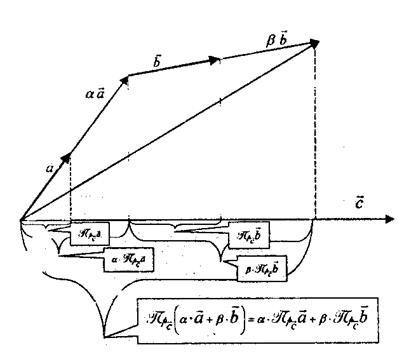
где φ – угол между Можно показать (смотри нижний рисунок), что
т.е. проекция линейной комбинации векторов равна линейной комбинации проекций этих векторов.
Произведение векторов. Скалярное произведение.
Скалярным произведение векторов Обозначив скалярное произведение символами ( Можно показать, что скалярное произведение обладает следующими свойствами: 1. ( 3. Из них, частности, вытекает следующее
Правило вычисления скалярного произведения в декартовом базисе.
Для заданных в декартовом базисе {i¸ j¸ k} векторов
Эту формулу используют, в частности, когда применяют
Основные приложения скалярного произведения
Последнее означает, что в декартовом базисе координаты вектора и соответствующие проекции - суть одно и тоже. Пример. Для треугольника (рис.) с вершинами А (2,4,0)В (6,5,8), С (-4,6,3) найти
Векторное произведение
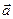 и и  называется новый вектор называется новый вектор  , наделенный свойствами: , наделенный свойствами:
1) его длина 2) вектор 3) векторы
Векторное произведение и обладает свойствами: 1) 2) 3) Из этих свойств вытекает
Правило вычисления векторного произведения
Для заданных в декартовом базисе {i¸j¸k} векторов
их векторное произведение может быть найдено по формуле
Из определения и свойств следует и Основные приложения векторного произведения Если S∆ - площадь треугольника построенного на векторах 1) 2) 3) Если h - высота пирамиды (параллелепипеда (призмы)), построенного (смотри следующий ниже рисунок) на векторах
Смешанное произведение векторов.
Смешанным произведением трех векторов Обозначив смешанное произведение символом ( ( В декартовом базисе смешанное произведение векторов
вычисляется по формуле ( Геометрически модуль смешанного произведения (
Пример. В пирамиде (рис. 9), построенной на векторах
Найти площадь основания, построенного на Решение:
С другой стороны
АЗЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. Уравнения прямой на плоскости.
 коллинеарный этой прямой. Условием принадлежности «текущей» (произвольной) точки М (х,у,z) к этой прямой является равенство коллинеарный этой прямой. Условием принадлежности «текущей» (произвольной) точки М (х,у,z) к этой прямой является равенство
(t - «коэффициент коллинеарности»). Переписанное в виде
(1)
оно именуется как векторно – параметрическое уравнение прямой. Из него вырастает целый букет» уравнений все той же прямой. Это: параметрические уравнения прямой -
; (2) каноническое уравнение прямой -
; (3)
уравнение прямой с нормальным вектором
(4)
уравнение прямой, проходящей через две точки М0 (х0,у0,z0) и М1 (х1,у1,z1) -
уравнение прямой с угловым коэффициентом k, содержащей точку М0 (х0,у0,z0) -
«школьное» уравнение прямой-
Общее уравнение прямой
Угол между прямыми.
Угол θ между прямыми (1) и (2) (рис. 11) с известными угловыми k1 и k2 может быть найден по формуле 
Отсюда, если прямые перпендикулярны, то

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , число
, число
 и
и 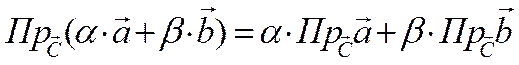
 и
и  называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.
называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. ,
, 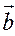 ) или
) или  +
+  ) ·
) ·  =
=  +
+ 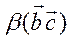 ;
;
 = (хb, уb, zb)
= (хb, уb, zb)

 , где К - основание высоты.
, где К - основание высоты.
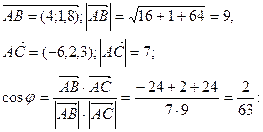



 ; а значит численно равна площади параллелограмма, построенного на этих векторах как на сторонах;
; а значит численно равна площади параллелограмма, построенного на этих векторах как на сторонах;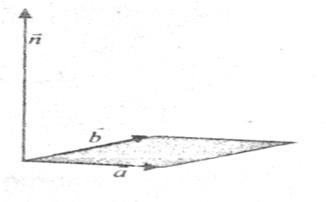
 или
или 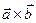
 ,
, ,
, .
.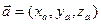 и
и 

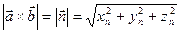 ,
, ,
, .
.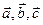 как на ребрах, то она может быть найдена по формуле
как на ребрах, то она может быть найдена по формуле




 ,
,  ,
, 


 .
.




 , содержащей точку М0 (х0,у0,z0) -
, содержащей точку М0 (х0,у0,z0) - ; (5)
; (5) ; (6)
; (6) ; (7)
; (7) . (8)
. (8)