
|
|
ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯПусть имеется выборка объема n со значениями признака х1 х2, х3, ..., хk. Построим статистическое распределение. Таблица 4
Для того чтобы охарактеризовать наиболее существенные свойства этого распределения, так же как и в теории вероятностей, используют средние показатели или, как их называют, выборочные числовые характеристики. Рассмотрим некоторые из них. 1. Выборочная средняя где п — объем выборки, хi ni взяты из табл. 4. Выборочная средняя Если дано распределение непрерывной случайной величины, то вместо хi берут середину интервала (xi, …, xi+1), т.е. Для упрощения вычисления выборочных характеристик удобно перейти от данных значений признака x1|, х2, х3,...,хk к условным значениям и1, и2,. и3,..., uk—по формуле т. е. ввести вспомогательную величину Можно показать, что при переходе к условным значениям признака по формуле зависимость, связывающая Действительно,
Пример.Дано статистическое распределение: Таблица 5
Найти Решение. Перейдем к условным значениям признака, приняв за C значение с наибольшей частотой, т. е. С=5. Далее находим h = xi-xi-1 = 2. Имеем
Составляем распределение условных значений признака. Таблица 6
Находим
Особенно выгодно применять формулу (4), если значения признака велики. 2. Выборочная и исправленная дисперсия.Одна числовая характеристика Составим таблицу отклонений Таблица 7
Найдем среднее значение отклонений
Следовательно, среднее значение отклонения Итак,
или Определение. Выборочной дисперсией называется среднее арифметическое значение квадратов отклонений признака от выборочной средней. Пример.Урожайность двух сортов А и В пшеницы, возделываемых на трех участках с одинаковыми условиями роста и развития, характеризуется следующими таблицами: сорт А сорт В
Найти дисперсии значений признака обоих сортов. Решение. Вычислим XB, YB, DX, DY. Находим
Как видим, дисперсия Dy как мера рассеяния или разброса урожайности сорта В относительно среднего значения YB в случае примерно одинаковых площадей больше, чем Dy, а это явление нежелательное. Из двух сортов лучшим является тот, урожайность которого более устойчива. По данным опыта сорт А предпочтительнее сорта В. Для вычисления выборочной дисперсии используют следующую формулу: т. е. дисперсия равна разности между средним значением квадрата и квадратом выборочной средней. Действительно,
Для облегчения вычисления дисперсии используют следующие свойства: 1°. Дисперсия не изменится, если все значения признака увеличить (уменьшить) на постоянное число. 2°. При умножении значений признака на постоянное число h ≠ 0 дисперсия умножается на h2. Выборочная дисперсия, как это показано в более подробных курсах (например, [4]), имеет систематическую ошибку, приводящую к уменьшению дисперсии. Чтобы это устранить, вводят поправку, умножая DB, на
или
На практике часто вместо этой формулы используют другую, ей равносильную, а именно:
При малых выборках S ощутимо отличается от DB, например, при n = 2 имеем S2=2DB. С возрастанием n исправленная дисперсия S2®DB. Уже при n = 30 дисперсии S2и DB различаются на 3%. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .При наличии повторяющихся значений признака
.При наличии повторяющихся значений признака , (3)
, (3) .
. , (4)
, (4) , где С–новое начало отсчета, обычно это значение признака с наибольшей частотой, h – масштаб.
, где С–новое начало отсчета, обычно это значение признака с наибольшей частотой, h – масштаб.
 , имеет вид
, имеет вид (5)
(5)




 , указывая соответствующие частоты.
, указывая соответствующие частоты.



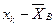
 . Имеем
. Имеем
 .
.
 (5)
(5)




 (6)
(6)
 . В результате получают исправленную дисперсию
. В результате получают исправленную дисперсию (7)
(7) (8)
(8)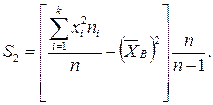 (9)
(9)