
|
|
Вывод производных основных элементарных функций12 Глава II. Дифференциальное исчисление функций одной переменной Производная функции Определение производной функции Пусть функция Определение. Производной функции
Если Если существуют только односторонние пределы при Если функция
Дифференцируемость функции, ее взаимосвязь с производной И непрерывностью функции Определение. Функция Если функция
Справедливо также обратное утверждение, если функция одной переменной
Следовательно, Рассмотрим, как связана дифференцируемость функции с ее непрерывностью. Если функция, дифференцируемая в точке, то она непрерывна в этой точке. Действительно, Однако, не всякая непрерывная функция является дифференцируемой. Например, функция
Непосредственное нахождение производной
Найти производные функций, используя определение производной. 1. 2. Геометрический смысл производной
Таким образом, производная функции Используем этот факт, запишем уравнение касательной в точке
Механический смысл производной
Пусть S = S(t) является функцией зависимости пути от времени. Тогда
Отсюда следует, что производная функции равняется мгновенной скорости изменения функции.
Правила дифференцирования функций
Пусть u = u(x) и v = v(х) – дифференцируемые функции. Получим формулы дифференцирования суммы, произведения и частного функций. При этом используем определение производной и свойства пределов. 1. Производная суммы (разности) функций.
2. Производная произведения функций.
3. Производная частного функций (v(х) ¹ 0).
4. Производная сложной функции
Правило нахождения производной сложной функции. Производная сложной функции равняется произведению производных составляющих функций; причем при нахождении производных составляющих функций их аргументы не изменяются. 5. Производные взаимно обратных функций
Следовательно, производные взаимно обратных функций являются обратными по величине.
Вывод производных основных элементарных функций Получим формулы для нахождения производных основных элементарных функций. 1.
2.
3.
4. При выводе формул нахождения производных обратных тригонометрических функций используем взаимосвязь производных взаимно обратных функций и формулы взаимосвязи тригонометрических функций. 5.
6.
7.
8.
9.
В частном случае, когда a = e, 10. При нахождении производной показательной функции
В частном случае, когда a = e 11. Производную степенной функции
В практических задачах часто встречаются производные от функций
12. Производная обобщенно-показательной (показательно-степенной) функции
= Как можно заметить производная обобщенно-показательной функции равняется сумме производных как показательной и как степенной функций. Например: 1) 2)
13. Производная функции, заданной неявно. Функция Пример 2.1. Найти производные функций 1) 2)
14. Производная функции, заданной параметрически. Функция называется заданной параметрически, если функция y и аргумент x заданы в виде функций, зависящих от некоторого параметра t, т. е.
Найдем производную данной функции в общем случае
Здесь предполагается, что функция Например, пусть функция в параметрической записи имеет вид
Исключим в этой системе параметр t. Получим
т. е. данная функция представляет окружность в параметрической записи. Найдем производную данной функции.
Сводка формул 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 непрерывна на отрезке
непрерывна на отрезке  и точка
и точка  является внутренней точкой этого отрезка.
является внутренней точкой этого отрезка. к приращению независимой переменной
к приращению независимой переменной  при
при  , если этот предел существует (конечный или бесконечный), т. е.
, если этот предел существует (конечный или бесконечный), т. е. .
. , то говорят, что функция
, то говорят, что функция  , то функция
, то функция  .
. , то
, то  называется производной функции на этом интервале.
называется производной функции на этом интервале. , где
, где 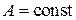 ,
, 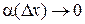 при
при  .
. , где
, где 
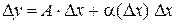 .
. , что соответствует определению 1 непрерывности функции в точке.
, что соответствует определению 1 непрерывности функции в точке. является непрерывной в точке x = 0 (рис. 16) , а ее производная
является непрерывной в точке x = 0 (рис. 16) , а ее производная  в точке x = 0 не существует (рис. 17). Следовательно,
в точке x = 0 не существует (рис. 17). Следовательно, 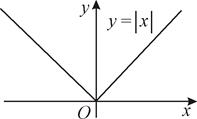 Рис. 16
Рис. 16
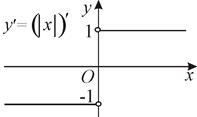 Рис. 17
Рис. 17
 . Производная постоянной равна нулю.
. Производная постоянной равна нулю.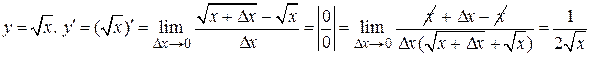 .
. Рис. 18
Рис. 18
 ,
где φ – угол наклона секущей
,
где φ – угол наклона секущей  , проходящей через точку
, проходящей через точку  к оси Оx.
При
к оси Оx.
При  и
и  ,
где a – угол наклона к оси Ох касательной.
,
где a – угол наклона к оси Ох касательной.
 равна тангенсу угла наклона касательной к графику этой функции в данной точке (рис. 18).
равна тангенсу угла наклона касательной к графику этой функции в данной точке (рис. 18).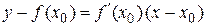 .
.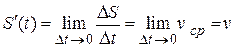 .
.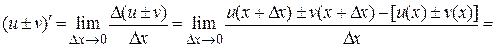

 .
.

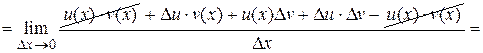
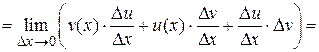

 .
.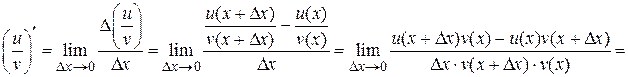
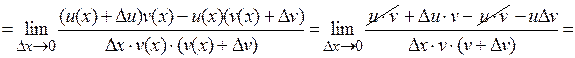
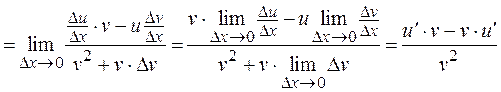 .
.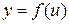 ,
, 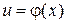 .
. .
. .
. .
.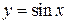 . При нахождении производной функции
. При нахождении производной функции 

 .
. . Используем формулы приведения и производную сложной функции, получим
. Используем формулы приведения и производную сложной функции, получим .
. . Используем формулу дифференцирования частного, получим
. Используем формулу дифференцирования частного, получим .
. .
.  .
. . Для
. Для 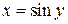 .
.
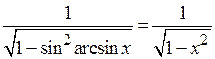 .
.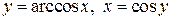 .
. .
. .
. 
 .
. .
. 
 .
. .При нахождении производной логарифмической функции используем определение производной и второй замечательный предел.
.При нахождении производной логарифмической функции используем определение производной и второй замечательный предел.
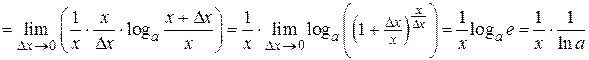 .
. .
.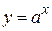 используем так называемое логарифмическое дифференцирование. Для этого логарифмируем равенство
используем так называемое логарифмическое дифференцирование. Для этого логарифмируем равенство  . Это равенство дифференцируем; при этом учитываем, что
. Это равенство дифференцируем; при этом учитываем, что  сложная функция.
сложная функция. .
. ,
, 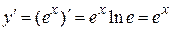 .
. найдем так же, используя логарифмическое дифференцирование.
найдем так же, используя логарифмическое дифференцирование. 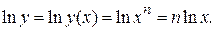
 .
.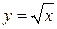 и
и 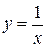 , которые полезно помнить.
, которые полезно помнить.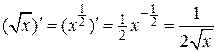 .
.  .
.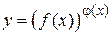 . Используем определение логарифма, представим функцию в виде
. Используем определение логарифма, представим функцию в виде  Эту функцию дифференцируем как сложную показательную функцию.
Эту функцию дифференцируем как сложную показательную функцию.
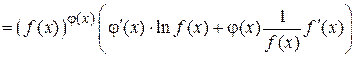 =
= .
.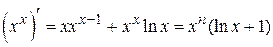 ;
;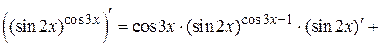
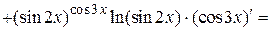
 .
. , не разрешенным относительно y. Чтобы найти производную функции
, не разрешенным относительно y. Чтобы найти производную функции  , заданную неявно, необходимо каждое слагаемое уравнения
, заданную неявно, необходимо каждое слагаемое уравнения  .
. , заданных неявно.
, заданных неявно. . Находим
. Находим  .
.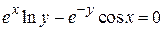 . Получаем
. Получаем  Þ
Þ Þ
Þ  .
.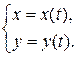
 .
. имеет обратную функцию
имеет обратную функцию  .
.
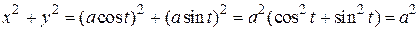 ,
,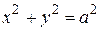 ,
, .
.