
|
|
Обобщённый алгоритм ЕвклидаДискретная математика для ФРТ
Введение В пособии рассматриваются следующие задачи: Основы теории целых чисел, комбинаторика, понятие о графах (дополнительный материал), булевы функции. Основы теории целых чисел
1. Деление с остатком
Определение
a, b Î Z, b > 0.
Поделить a на b с остатком – значит найти такие числа p и q, что a = bq + r, при этом 0≤r<b.
Примеры: 1. (Показать на доске) 25 = 4×6 + 1 2. (Решить самостоятельно) -25 = -5×6 + 5
Докажем единственность деления с остатком. В самом деле, если Тогда Если левая часть не равна 0, то её модуль не меньше b, поскольку умножаем b на ненулевое целое число. С другой стороны, оба остатка меньше b, поэтому модуль разности в правой части меньше b. Противоречие! Поэтому левая часть равна 0, и два представления совпали.
Пример. Найдутся два целых числа, составленных из одних единиц, которые дают одинаковый остаток при делении на 37.
Решение Возьмём 38 чисел, составленных из одних единиц. Поскольку остатков от деления на 37 всего 37, то хотя бы у двух чисел совпадут остатки.
Задачи.
1. Найти остаток от деления 22000 на 3. Решение
Раскрыв скобки, получим много слагаемых, кратных 3, и одно слагаемое, равное 1. Поэтому остаток равен 1.
Ответ: 1.
2. а) доказать, что найдутся два числа, составленные из единиц, разность которых кратна 5007. б) доказать, что найдётся одно число, составленное из единиц и кратное 5007. Решение.
а) Возьмём 5008 чисел, составленных из одних единиц. Поскольку остатков от деления на 5007 всего 5007, то хотя бы у двух чисел совпадут остатки, следовательно, их разность будет кратна 5007. б) Рассмотрим эту разность. В начале её некоторое количество единиц, затем одни нули. Поскольку нули означают умножение на степень числа 10, а это число взаимно просто с 5007, то нули не помогают для делимости на 5007, их можно отбросить. Поэтому число из единиц делится на 5007.
Делимость
Говорят, что
Свойства делимости 1. a | b и b | c Þ a | c. 2. a | b и a | c Þ a | (b ± c). 3. a | b и a | c Þ a | (b ± kc), k Î Z.
Наибольший общий делитель и наименьшее общее кратное
Определение.
d = НОД (a1, … an), если d – наибольшее целое число, на которое делятся все a1, … an. m = НОК (a1, … an), если m – наименьшее целое число, которое делится на все a1, … an.
Алгоритм Евклида
Пример. НОД (72, 96) = НОД (72, 96 - 72) = НОД (72, 24) = 24. Идея вычисления наибольшего общего делителя в том, что некоторые числа заменяем их линейными комбинациями таким образом, что числа уменьшаются, а наибольший общий делитель остаётся прежним.
Приведём более строгое описание работы алгоритма.
Теорема
Множество общих делителей не меняется при элементарных преобразованиях набора (a1, … an), то есть при замене ai числом ai - q× ak. В самом деле, если некоторое число d было общим делителем набора (a1, … an), то все линейные комбинации этих чисел, в том числе ai - q× ak, делятся на d. Аналогично, если число d1 является общим делителем для набора, в котором провели замену, то оно является делителем q× ak, а, следовательно, является делителем ai. Следовательно, является делителем исходного набора.
Пример
276 = 84 × 3 + 24 84 = 24 × 3 + 12 24 = 12 × 2
НОД (276, 84) = НОД (84, 24) = НОД (12, 24) = НОД (12, 0) = 12
Общая формула алгоритма для двух чисел.
a = bq1 + r1 b = r1q2 + r2 r1 = r2q3 + r3 r2 = r3q4 + r4 … В конце концов остаток при делении окажется равен нулю, поскольку остатки уменьшаются с каждым шагом, и все они положительные. rk-1 = rkqk+1 + rk+1 rk = rk+1qk+2
Тогда НОД (a, b) = rk+1 (то есть наибольший общий делитель равен последнему ненулевому остатку).
Алгоритм Евклида относится к так называемым «быстрым» алгоритмам, поскольку на каждом шаге остаток уменьшается, по крайней мере, в 2 раза, поэтому за сравнительно небольшое количество шагов алгоритм заканчивает работу.
Для трёх чисел вычисление наибольшего общего делителя может быть, например, таким.
НОД (65, 182, 130) = НОД (65, 182, 0) = НОД (65, 52, 0) = НОД (13, 0, 0) = 13.
Упражнения.
1. Найти НОД (111 111, 1111) Решение:
Таким образом, НОД (111111, 1111) = 11.
2. Найти НОД (98, 147, 112) Решение. НОД (98, 147, 112) = НОД (98, 147, 14) = НОД (0, 147, 14) = НОД (0, 7, 14) = НОД (0, 7, 0) = 7
Обобщённый алгоритм Евклида (Линейное представление наибольшего общего делителя).
Если d = НОД (a, b), то существуют такие целые числа x и y, что d = ax + by.
Пример.
1 = 7 x + 11 y
1 = 11 × 2 – 7 × 3
Теперь выведем общий метод вычисления линейного представления наибольшего общего делителя набора из произвольного количества чисел.
Определение
Линейным представлением числа d через набор чисел a1, a2, … , an называется выражение d = x1a1 + …. + xnan.
Теорема
d = НОД (a1, … , an) Þ $ x1, …. , xn: d = x1a1 + …. + xnan.
Лемма Элементарное преобразование ai’ = ai – kaj не меняет линейную оболочку набора.
(Линейной оболочкой набора (a1, … , an) называют множество всех выражений вида x1a1 + …. + xnan)
Доказательство леммы
Каждое число из линейной оболочки (a1’, … , an’) входит в линейную оболочку (a1, … , an), и наоборот.
На самом деле, если число представлено в виде t1a1’ + … + tnan’, то представив число ai’ в виде ai – kaj, выразим все a1’, … , an’ через (a1, … , an) и получим коэффициенты разложения для системы (a1, … , an). Аналогично находим представление по системе (a1’, … , an’), если известно разложение по системе (a1, … , an).
Доказательство теоремы
Линейная оболочка набора (a1, … , an) совпадает с линейной оболочкой (0, 0, …, d) (это следует из применения алгоритма Евклида).
Примеры.
276 = 84 × 3 + 24 84 = 24 × 3 + 12 24 = 12 × 2
Раскручивая последовательность вычислений в обратную сторону, получим:
24 = 276 – 84 × 3 12 = 84 – 24 × 3 = 84 – (276 – 84 × 3) × 3 = 84 × 10 – 276 × 3
Итак, 12 = 84 × 10 – 276 × 3
Общая формула:
a = bq1 + r1 b = r1q2 + r2 r1 = r2q3 + r3 r2 = r3q4 + r4 … rk-2 = rk-1qk + rk rk-1 = rkqk+1 + rk+1 rk = rk+1qk+2
Отсюда получаем: rk+1 = rk-1 – rkqk+1
То есть мы выразили rk+1 = НОД (a, b) через два предыдущих остатка: rk и rk-1. Далее, воспользовавшись тем, что rk = rk-2 – rk-1qk, выразим rk+1 в виде rk+1 = rk-1 – rkqk+1 = rk-1 – (rk-2 – rk-1qk)qk+1. (1)
В этом случае получим линейное представление rk+1 = НОД (a, b) через остатки rk-1 и rk-2. Затем выразим rk-1 через остатки rk-2 и rk-3, подставив полученное представление в формулу (1), получим представление НОД (a, b) через остатки rk-2 и rk-3. Продолжим процесс до тех пор, пока не получим линейное представление НОД (a, b) через a и b.
Свойства НОД 1. Если
Доказательство: Обозначим
Умножим это равенство на
2. Если
Согласно предыдущему:
Деля это равенство на
В частности,
3. Если Действительно, так как
Умножим это равенство на
Так как 4. Если В силу равенства (1) всякий общий делитель Свойства НОК. 1.Всякое кратное чисел 2. Свойства кратного двух чисел. Пусть Тогда Пусть Тогда
Но Получаем формулу:
При любом целом При
Следовательно
Доказаны следующие теоремы. 1) Совокупность общих кратных двух чисел совпадает с совокупностью кратных наименьшего общего кратного этих чисел. 2) Это наименьшее кратное равно произведению чисел, поделенному на их наибольший общий делитель. 3. Наименьшее общее кратное трех и более чисел находится по следующему правилу.
Если числа И вообще, если

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



 (a делится на b) или b | a (b делит a), если существует q такое, что a = bq.
(a делится на b) или b | a (b делит a), если существует q такое, что a = bq.
 любое положительное число, то
любое положительное число, то .
. . Имеем разложение:
. Имеем разложение: .
.
 является делителем чисел
является делителем чисел  и
и  и является линейной комбинацией этих чисел. Следовательно,
и является линейной комбинацией этих чисел. Следовательно,  .
. - любой делитель
- любой делитель  и
и  , то
, то
 .
.
 делится на
делится на  делится на
делится на  и
и  , такие что
, такие что .
. . (1)
. (1) .
. делит
делит  . Но и
. Но и  называется их общим кратным. Наименьшее из общих кратных называется наименьшим общим кратным чисел
называется их общим кратным. Наименьшее из общих кратных называется наименьшим общим кратным чисел  .
.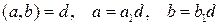 .
. .
. - кратное
- кратное  . Но
. Но  - целое число.
- целое число. , поэтому
, поэтому  .
. .
.
 получаем наименьшее общее кратное:
получаем наименьшее общее кратное: .
.
 .
. и
и  .
. - попарно просты, то
- попарно просты, то