
|
|
Типовые нечеткие логические операцииНечеткие логические операции могут быть введены различными способами. Рассмотрим типовые нечеткие логические операции, используемые в прикладных задачах управления. Поскольку значения истинности нечетких предикатов описываются нечеткими множествами, то для введения операций нечеткой логики будем использовать операции нечетких множеств. Определение: нечеткая конъюнкция (Fuzzy conjunction или fuzzy AND). Значение истинности нечеткой конъюнкции
где Определение: нечеткая дизъюнкция: (Fuzzy disjunction или fuzzy OR). Значение истинности нечеткой конъюнкции
где Определение:нечеткое отрицание (Fuzzy negation). Значение истинности нечеткого отрицания
где Нечеткая импликация или нечеткое правило Нечеткая импликация или нечеткое правило (Fuzzy implication или a fuzzy rule) представляет собой следующее выражение: ЕСЛИ где A и B - лингвистические переменные, определенные нечеткими множествами на универсумах C и U соответственно. В символьной форме запись имеет следующий вид: Часть «ЕСЛИ» (х есть A) называется антецедентом (the antecedent) или посылкой. Часть «ТО» ( Определение: Нечеткая импликация (Fuzzy implication).Значение истинности нечеткой импликации
где Интерпретация нечеткой импликации, данная в этом определении, называется импликацией Мамдани (Mamdani implication). На рис. 2.9 показаны различные интерпретации нечеткой импликации R.
Рис. 2.9.(а, б) Две интерпретации нечеткой импликации Первая интерпретация (рис. 2.9 (а)) представляет импликацию Мамдани: Мы будем использовать первую интерпретацию. При этом нечеткое множество R может быть описано как
где * есть оператор нечеткой конъюнкции ( fuzzy AND operator), т.е.
Примечание. Как принято в литературе по нечетким множествам, знаки интеграла « Примечание. Заметим, что в литературе предложено много определений нечетких логических операций. В общем случае, эти операции называются Импликация Лукашевича (Lukasiewicz’s implication):
Импликация Ларсена (Larsen implication):
Импликация Заде (Zadeh implication):
Популярной альтернативой введенным выше определениям нечеткой конъюнкции и дизъюнкции являются следующие:
Процесс нечеткого вывода Прежде, чем рассмотреть процесс нечеткого вывода, обсудим модель процесс рассуждений (reasoning process) в общем виде, который проиллюстрирован на рис. 2.10. Примечание. Представленные на рис. 2.10 английские термины имеют следующий перевод: Current data – текущие входные данные; Reasoning scheme – схема рассуждения; KB (Knowledge Base) – БЗ; A set of Rules- множество правил; New Facts – новые факты.
Рис. 2.10. Общая схема процесса рассуждений
В общем случае, процесс рассуждений, или вывод (inference), состоит из двух этапов: 1. сопоставление (matching) входных данных (A1,A2,…) с левыми частями правил, содержащихся в БЗ, и 2. вывод (Inferring) выходных данных (фактов) (B1, B2,…) с использованием законов вывода. Рассмотрим вначале классический вывод. Классические схемы вывода Обратимся к классической пропозициональной логике (classical propositional logic) или логике высказываний. Наиболее популярными законами вывода в логике высказываний являются так называемые законы «модус поненс» (modus ponens) и «модус толленс» (modus tollens), приведенные ниже. Modus ponens правило вывода: которое означает следующее: если имеется правило Другими словами, зная, что высказывания Modus tollens правило вывода: которое означает следующее: если имеется правило Другие законы вывода также используются в логике высказываний, например, следующие: Закон силлогизма (Law of syllogism): Закон противоположностей (Law of contra positive): Закон двойного отрицания (Law of double negation): Перепишем теперь традиционный закон вывода modus ponens следующим образом: Посылка 1 (входной факт): Правило: ЕСЛИ Заключение: Отметим главные особенности классической схемы вывода: · мы делаем точное сопоставление (exact matching) входных данных (фактов) с левыми частями правил (импликаций); · мы имеем дело с двузначными величинами истинности (истинно/ложно) входных и выходных данных. Нечеткий вывод Процесс нечеткого вывода показан на рис. 2.11. Мы сопоставляем нечеткие входные данные с левыми частями нечетких правил (нечеткой импликации) и нечеткий выход получаем с применением нечеткого закона вывода. Рассмотрим закон вывода в нечеткой логике. Этот закон называется обобщенный «модус поненс» (generalized modus ponens):
что означает следующее: если мы имеем нечеткое правило Перепишем эту схему вывода следующим образом: Посылка 1 ( нечеткий вход): Нечеткое правило: ЕСЛИ Нечеткое заключение:
Рис. 2.11. Процесс нечеткого вывода
Таким образом, мы можем видеть две основные особенности нечеткой схемы вывода. · мы делаем приближенное сопоставление (approximate matching) входных данных (фактов) с левыми частями правил (импликаций); · мы имеем дело с непрерывными величинами истинности (continuous-valued truth values) входных и выходных данных. Сформулируем теперь основную проблему нечеткого логического вывода: если мы знаем функции принадлежности входных данных Нечеткий вывод, основанный на правиле max-min композиции Итак, опишем следующую проблему. Пусть Рассмотрим следующий нечеткий вывод: Посылка 1 ( нечеткий вход): Нечеткое правило: ЕСЛИ Нечеткое заключение: Поставим следующую задачу: построить нечеткое множество Рассмотрим метод ее решения. Нечеткое правило может быть рассмотрено как нечеткое бинарное отношение в двумерном пространстве Для построения множества 1. построить цилиндрическое расширение (cylindrical extension) с основой 2. найти пересечение 3. сделать проекцию пересечения Запишем эти шаги формально. Пусть
Но из определению пересечения нечетких множеств имеем
Далее, проецируя
Формула (2.1) называется max-min композицией (max-min composition). Обозначим эту композицию символом “
Если мы выберем в качестве операции нечеткого пересечения операцию умножения (функций принадлежности), то мы будем иметь правило max-product композиции:
Формулы (2.1) и (2.3) являются наиболее часто применяемыми в нечетком выводе. Пример: Нечеткий вывод с единственным нечетким правилом, в котором всего один антецедент. Рассмотрим простейший случай, когда мы имеем в БЗ всего одно правило: Нечеткое правило: ЕСЛИ Правило содержит в левой части только один антецедент «ЕСЛИ Перепишем формулу (2.2) с учетом интерпретации для нечеткой импликации в виде:
Тогда
= Будем называть Примечание. В литературе этот параметр Пример: Нечеткий вывод с единственным нечетким правилом, в котором два антецедента. Рассмотрим нечеткое правило с двумя антецедентами: “ЕСЛИ Данное нечеткое правило представляет тернарное нечеткое отношение R, которое может быть определено следующими функциями принадлежности
Результирующее нечеткое множество
Используя (2.5) и расширение (2.2) на случай (2.6), мы можем вычислить
Механизм вычисления формулы (2.7) показан графически на рис. 2.12.
Рис. 2.12. Простая графическая интерпретация схемы нечеткого вывода на основе max-min композиции Опишем вычисления в формуле (2.7), представленных на рис. 2.12. Находим Примечание. Рассмотрим другой тип нечеткого правила: “ЕСЛИ Тогда степень активации правила w вычисляется как максимум из величин w1 и w1. Пример: Нечеткий вывод с множеством нечетких правил, в которых много антецедентов. В этом случае схема нечеткого вывода выглядит следующим образом: Посылка 1 (вход): Правило 1: ЕСЛИ Правило 2: ЕСЛИ Заключение (выход):
Будем строить нечеткое множество
Так как оператор max-min композиции обладает дистрибутивным свойством относительно операции «
где Итак, конечный результат вывода строится как сумма (т.е. мах) нечетких множеств Механизм вычисления формулы (2.9) показан графически на рис. 2.13. Этот метод нечеткого вывода называется также как минимаксный (min-max) метод нечеткого вывода. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определяется следующим образом:
определяется следующим образом: =
= 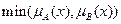 ,
, - значения истинности нечетких предикатов A, B соответственно.
- значения истинности нечетких предикатов A, B соответственно. определяется следующим образом:
определяется следующим образом: =
=  ,
, определяется следующим образом:
определяется следующим образом: =
=  ,
, - значение истинности нечеткого предиката A.
- значение истинности нечеткого предиката A. есть
есть 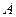 , ТО
, ТО  есть
есть  ,
, .
. определяется следующим образом:
определяется следующим образом: =
=  ,
, есть операция нечеткой конъюнкции (fuzzy AND operation) и
есть операция нечеткой конъюнкции (fuzzy AND operation) и  соответственно.
соответственно. (а)
(а)
 (б)
(б)
 . Вторая интерпретация (рис. 2.9,б) представляет так называемую материальную импликацию, или Булеву импликацию и означает следующее:
. Вторая интерпретация (рис. 2.9,б) представляет так называемую материальную импликацию, или Булеву импликацию и означает следующее: 
 B =
B =  ,
, =
=  .
. » и деления «/» в приведенной выше формуле используется только для указания непрерывной совокупности точек
» и деления «/» в приведенной выше формуле используется только для указания непрерывной совокупности точек  .
. -нормы и
-нормы и  ;
; ;
; .
. .
.
 ,
, ,
, (не
(не  также верно, то есть высказывание
также верно, то есть высказывание  ;
; ;
; .
. ,
, (
(  ), то мы можем сделать выходное заключение
), то мы можем сделать выходное заключение  (
(  ).
).
 и функции принадлежности левых и правых частей нечеткого правила
и функции принадлежности левых и правых частей нечеткого правила  , то как определить функцию принадлежности заключения
, то как определить функцию принадлежности заключения  ?
? с некоторой функцией принадлежности
с некоторой функцией принадлежности  . Следовательно, R есть двумерное нечеткое множество с двумерной функцией принадлежности
. Следовательно, R есть двумерное нечеткое множество с двумерной функцией принадлежности  . Это означает, что мы расширили домен
. Это означает, что мы расширили домен  .
. ,
, 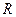 соответственно.
соответственно. .
. =
=  . (2.1)
. (2.1) ” и представим ее в символьной форме как:
” и представим ее в символьной форме как: . (2.2)
. (2.2)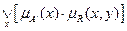 . (2.3)
. (2.3) =
= . (2.4)
. (2.4) - степень активации правила.
- степень активации правила. И
И  ТО
ТО  .”
.” (2.5)
(2.5) может быть представлено как:
может быть представлено как: (2.6)
(2.6)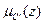 как:
как:

 (2.7)
(2.7)

 и
и 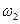 (степени активации правила) следующим образом:
(степени активации правила) следующим образом:  , and
, and  ,
, И
И  ТО
ТО 
 И
И  ТО
ТО 

 Рис. 2.13. Графическая интерпретация схемы нечеткого вывода на множестве правил
Рис. 2.13. Графическая интерпретация схемы нечеткого вывода на множестве правил (2.8)
(2.8)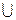 », перепишем (2.8) следующим образом:
», перепишем (2.8) следующим образом: , (2.9)
, (2.9) and
and  - результирующие нечеткие множества для правил 1 и 2.
- результирующие нечеткие множества для правил 1 и 2.