
|
|
Эйлера — кинематические уравнения Эйлера12 По заданным уравнениям движения (5.1) можно определить мгновенную угловую скорость Поскольку при движении НМС с одной неподвижной точкой изменяются все три угла Эйлера с угловыми скоростями
Используя рис. 56, спроектируем выражение (5.2) на оси неподвижной системы координат
Используя рис. 56, спроектируем также выражение (5.2) на оси подвижной системы координат Охуz:
Формулы (5.3) и (5.4) при известных уравнениях движения НМС (5.1) позволяют определить модуль угловой скорости:
Направление угловой скорости можно определить по известным формулам через косинусы углов, которые составляет этот вектор с осями координат.
Угловое ускорение НМС Так как движение НМС с одной неподвижной точкой может быть представлено в каждый момент времени, как мгновенное вращательное движение с угловой скоростью По смыслу векторной производной
Рис. 59 Так как
то, взяв производную по времени от проекций угловой скорости на оси неподвижной системы координат (5.3), можно вычислить проекции углового ускорения Модуль углового ускорения
Направление углового ускорения
Скорость точки НМС Так как в каждый момент времени движение НМС с одной неподвижной точкой представляет собой мгновенное вращательное движение относительно мгновенной оси, проходящей через эту неподвижную точку, то, используя векторную формулу Эйлера (3.13), для каждого момента времени можно записать:
Модуль скорости определяется соотношением:
где Направление скорости · · скорость Скорость
Рис. 60 Представляя выражение (5.7) в виде определителя, получим:
где Разлагая определитель по элементам первой строки, получим проекции скорости
Представляя выражение (5.7) в виде определителя, получим также:
где x, y, z – координаты точки B в подвижной системе координат, а Разлагая определитель по элементам первой строки, получим проекции скорости
где х, у, z – величины постоянные, так как положение точки относительно осей Охуz, неизменно связанных с движущейся НМС, с течением времени не изменяется. Формулы (5.10) и (5.12) называются формулами Эйлера. Ускорение точки НМС Ускорение точки В, принадлежащей НМС, имеющую одну неподвижную точку, можно найти, взяв производную по времени от выражения (5.7):
или
Первое слагаемое ускорения точки:
называется вращательным ускорением точки. Величина вращательного ускорения точки определяется формулой:
где Направление вращательного ускорения точки определяется правилом векторного произведения: · ·ускорение
Рис. 61 В отличие от случая вращения НМС вокруг неподвижной оси угловое ускорение Второе слагаемое ускорения точки:
называется осестремительным ускорением точки. Величина осестремительного ускорения точки с учетом (5.8) определяется формулой:
Направление осестремительного ускорения МТ определяется правилом векторного произведения: · · ускорение Так как Таким образом,
а модуль ускорения
Подставив соотношения (5.15) и (5.16) в формулу (5.19), получим:
Ускорение 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. ,
,  ,
,  , то угловая скорость
, то угловая скорость  ,
,  ,
, 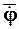 (глава 8):
(глава 8):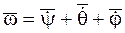 . (5.2)
. (5.2) :
: (5.3)
(5.3) (5.4)
(5.4) .
. относительно мгновенной оси вращения, проходящей через неподвижную точку, а
относительно мгновенной оси вращения, проходящей через неподвижную точку, а  изменяется с течением времени не только по модулю, но и по направлению, то направление углового ускорения
изменяется с течением времени не только по модулю, но и по направлению, то направление углового ускорения  не совпадает с направлением
не совпадает с направлением  (в отличие от вращательного движения НМС вокруг неподвижной оси и плоскопараллельного движения НМС).
(в отличие от вращательного движения НМС вокруг неподвижной оси и плоскопараллельного движения НМС). в соответствующей точке (рис. 59) (по аналогии с направлением скорости по касательной к годографу радиус-вектора
в соответствующей точке (рис. 59) (по аналогии с направлением скорости по касательной к годографу радиус-вектора  ,
, 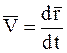 ).
).
 (5.5)
(5.5) на неподвижные оси через углы Эйлера. Аналогично можно найти проекции углового ускорения на подвижные оси координат.
на неподвижные оси через углы Эйлера. Аналогично можно найти проекции углового ускорения на подвижные оси координат. определяется формулой:
определяется формулой: (5.6)
(5.6) можно определить через косинусы углов, которые составляет этот вектор с осями координат.
можно определить через косинусы углов, которые составляет этот вектор с осями координат. . (5.7)
. (5.7) , (5.8)
, (5.8) rВ×sina – кратчайшее расстояние от рассматриваемой точки до мгновенной оси вращения.
rВ×sina – кратчайшее расстояние от рассматриваемой точки до мгновенной оси вращения. определяется правилом векторного произведения:
определяется правилом векторного произведения: (следовательно, скорость
(следовательно, скорость  );
); был виден против хода часовой стрелки (рис. 60).
был виден против хода часовой стрелки (рис. 60).
 , (5.9)
, (5.9) — координаты точки B в неподвижной системе координат, а
— координаты точки B в неподвижной системе координат, а  — единичные орты неподвижной системы координат.
— единичные орты неподвижной системы координат. (5.10)
(5.10) , (5.11)
, (5.11) – единичные орты подвижной системы координат.
– единичные орты подвижной системы координат. (5.12)
(5.12)
 . (5.13)
. (5.13) (5.14)
(5.14) , (5.15)
, (5.15) = rВ sin b (рис. 61).
= rВ sin b (рис. 61). (следовательно, ускорение
(следовательно, ускорение  перпендикулярно также отрезку
перпендикулярно также отрезку 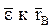 был виден против хода часовой стрелки (рис. 61).
был виден против хода часовой стрелки (рис. 61).
 при сферическом движении НМС не лежит на той же прямой, что и угловая скорость
при сферическом движении НМС не лежит на той же прямой, что и угловая скорость  , а направлено по касательной к годографу угловой скорости
, а направлено по касательной к годографу угловой скорости  перпендикулярно не к радиусу мгновенного вращения
перпендикулярно не к радиусу мгновенного вращения  , представляющему собой кратчайшее расстояние от точки до мгновенной оси вращения, а к отрезку
, представляющему собой кратчайшее расстояние от точки до мгновенной оси вращения, а к отрезку  (5.16)
(5.16) . (5.17)
. (5.17) ;
; направлено так, чтобы, глядя с конца этого вектора, поворот от
направлено так, чтобы, глядя с конца этого вектора, поворот от  к
к  был виден против хода часовой стрелки (рис. 61).
был виден против хода часовой стрелки (рис. 61).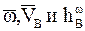 три взаимно перпендикулярных направления (рис. 60), то осестремительное ускорение
три взаимно перпендикулярных направления (рис. 60), то осестремительное ускорение 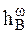 к мгновенной оси вращения (рис. 61).
к мгновенной оси вращения (рис. 61). , (5.18)
, (5.18)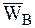 , как диагональ параллелограмма, построенного на ускорениях
, как диагональ параллелограмма, построенного на ускорениях  . (5.19)
. (5.19) .
.