
|
|
СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИУпругая твёрдая среда называется линейной и изотропной в том случае, если напряжения в ней линейно связаны с деформациями, а механические свойства среды не зависят от направления. В такой среде главные оси напряжений и деформаций совпадают. Связь между напряжениями и деформациями удобно записать в системе координат, связанной с главными осями:
где упругие модули l и G (модуль сдвига) называются параметрами Ламе. Свойства среды таковы, что от действия компонент деформации e возникает напряжение (l+2G)e в том же направлении и напряжения le в других взаимно перпендикулярных направлениях:
где Е (модуль Юнга, меняется для горных пород в пределах 10¸100 ГПа) и n (коэффициент Пуассона, меняется в пределах 0.1¸0.4) - материальные параметры среды. Главная компонента напряжения s создаёт деформацию s/E в направлении своего действия и деформации - ns/E в двух других взаимно перпендикулярных направлениях. Упругие свойства среды характеризуют, задавая l и G или E и n. Эти параметры не являются независимыми. Одноосное напряжённое состояние. В этом случае отлично от нуля только одно главное напряжение, например, s1. s2 = s3 = 0 , тогда
Отсюда видно, что напряжение s1 вызывает не только деформацию e1 в направлении своего действия, но и деформации в перпендикулярных направлениях e2 и e3. Если s1 - напряжение сжатия, то e1 - укорочение, а e2 и e3 - удлинения и наоборот. Эти деформации показаны на рис. 5.6, где элемент dxdydz стал короче в направлении оси y, но толще в направлении осей х и z. В соответствии с равенствами (5.3.4) - (5.3.6)мы можем написать
Сравнивая это равенство с (5.3.7), получаем
Из (5.3.1) и (5.3.7)находим
совместно с (5.3.8) для модуля Юнга получаем
С помощью (5.3.9) - (5.3.11) выражаем l и G через E и n:
В случае одноосного сжатия или растяжения соотношение (5.3.8) превращается в закон Гука:
Линейно-упругое тело называется иначе Гуковским телом. Относительное изменение объёма (дилатация D) определяется в этом случае выражением
Из формулы видно, что уменьшение объёма, происходящее за счёт сокращения размера в направлении действия напряжения, компенсируется увеличением объёма за счёт расширения в перпендикулярных направлениях. Из выражения (5.3.15) можно определить коэффициент Пуассона для несжимаемой среды, объём которой не меняется под действием приложенного напряжения. Чтобы это реализовать, при одноосном сжатии n должно быть равно ½. Под действием одноосного сжатия несжимаемая среда сокращается в направлении приложенного напряжения и расширяется на величину, вдвое меньшую в каждом из перпендикулярных направлений. Одноосная деформация. Состояние одноосной деформации характеризуется тем, что отличной от 0 является только одна главная компонента деформации, например, e1.Тогда (5.3.1) - (5.3.3) дают
а (5.3.4) - (5.3.6) упрощаются следующим образом:
Плоское напряжённое состояние. Возникает тогда, когда имеется только одно нулевое главное напряжение, например, s3 = 0,s2 ¹ 0,s1¹ 0. Тонкая пластина нагружена с боков. Определим компоненты деформации (5.3.4) - (5.3.6)
Плоская деформация. В этом случае равна нулю только одна главная деформация, например, e3 = 0.
На (рис.5.7) длинная балка жёстко зажата между двумя стенками, которые не позволяют ей расширяться или сжиматься в продольном направлении. Кроме того, вдоль всей длины на балку действуют равномерно распределённые напряжения s1и s2. (5.3.1)-(5.3.3) в этом случае становятся: s1 = (l + 2G)e1 + le2; s2 = le1 + (l + 2G)e2; s3 = l(e1 + e2). Из равенства (5.3.6) следует s3 = n(s1 + s2 ),что совместно с (5.3.7) и (5.3.9) даёт
ОСНОВЫ ГИДРОДИНАМИКИ ОСНОВНЫЕ ПОЛОЖЕНИЯ Задачи гидродинамики делятся на два основных класса: внутренние и внешние. К внешним задачам относятся задачи обтекания тела потоками жидкости или газа, или о движении тела в жидкой или газообразной среде. Внешними задачами являются задачи, связанные с полётами самолётов, снарядов и других тел, движущихся в атмосфере. Внутренние задачи занимаются движением жидкости в каналах. В этот класс задач входят такие, как: 1. течение жидкостей в трубопроводах (водопровод, газо-и нефтепроводы, кровеносная система, тепло и газоснабжение); 2. течение воды в открытых каналах и реках (ирригационные и осушительные системы, расчёт паводков, судопропускные сооружения и т.д.). При решении внешней задачи основной акцент делается на определение силового взаимодействия потока и тела. Определение силы, действующей со стороны набегающего потока, или силы сопротивления движению тела в жидкости - цель таких задач. Поэтому при анализе и решении внешних задач, как правило, используются уравнения, выражающие закон изменения количества движения: дифференциальные уравнения Навье - Стокса или Рейнольдса, а также интегральные формы этого закона. При решении внутренней задачи чаще всего стараются определить потери энергии в потоке жидкости. Здесь используются уравнения, выражающие закон изменения энергии, чаще всего в виде различных форм уравнения Бернулли. В основе гидродинамики, как части гидромеханики, положены три основных закона механики: I. закон сохранения массы; II. закон сохранения количества движения (импульса); III. закон сохранения энергии. Эти законы формулируются для конечных объёмов (размеры ограничены и оговорены). В МСС используются два подхода к описанию движения сплошной среды: Лагранжев и Эйлеров. Соответственно при Лагранжевом подходе используется движующиеся (материальные, индивидуальные) объемы Законы гидродинамики для конечных объёмов часто упрощаются с учётом конкретных условий на поверхностях, ограничивающих данный объём. Такие упрощенные уравнения используются в разделе, называемом гидравликой. По сути, это теоретические основы технической механики жидкости. Они особенно эффективны, когда исследуются интегральные (осреднённые по времени и пространству) гидромеханические характеристики потоков. В том случае, когда есть необходимость определять гидромеханические характеристики и величины в каждой точке объёма жидкости, используют дифференциальные уравнения. Они тоже являются фундаментальными законами механики, но относятся к точке сплошной среды. Если эти уравнения дополнить каким-либо реологическим законом, то можно определить структуру поля скорости и напряжённое состояние в любой точке потока жидкости. Практическое использование этих уравнений, в зависимости от изложенных здесь подходов, преобразуется из одного вида в другой с помощью теоремы Остроградского - Гаусса. Так при выводе гидравлических уравнений объёмные интегралы заменяются на поверхностные с тем, чтобы использовать особенности условий на поверхностях, ограничивающих поток, для упрощения уравнений. При выводе дифференциальных уравнений, наоборот, поверхностные интегралы заменяются на объёмные, чтобы можно было исследовать гидромеханические величины в точках внутри потока. При этом условия на границах потока вводятся как граничные или краевые условия для дифференциальных уравнений.
ЗАКОН СОХРАНЕНИЯ МАССЫ Выделим в пространстве контрольный материальный объём Масса бесконечно малого объёма
Согласно закону сохранения массы, при движении жидкого объёма его масса остаётся неизменной. Изменение во времени гидромеханической характеристики, относящейся к движущемуся жидкому объёму, который содержится в начальный момент внутри контрольной поверхности .

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (5.3.1)
, (5.3.1) , (5.3.2)
, (5.3.2) , (5.3.3)
, (5.3.3) , (5.3.4)
, (5.3.4) , (5.3.5)
, (5.3.5) , (5.3.6)
, (5.3.6) . (5.3.7)
. (5.3.7) Рис. 5.6. Деформация под действием
одноосного сжатия
Рис. 5.6. Деформация под действием
одноосного сжатия
 (5.3.8)
(5.3.8) . (5.3.9)
. (5.3.9) , (5.3.10)
, (5.3.10) . (5.3.11)
. (5.3.11) , (5.3.12)
, (5.3.12)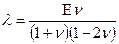 . (5.3.13)
. (5.3.13)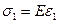 (5.3.14)
(5.3.14) (5.3.15)
(5.3.15) (5.3.16)
(5.3.16) , (5.3.17)
, (5.3.17) , (5.3.18)
, (5.3.18)  . (5.3.19)
. (5.3.19) Рис. 5.7. Плоское напряжённое состояние
Рис. 5.7. Плоское напряжённое состояние
 , (5.3.20)
, (5.3.20) , (5.3.21)
, (5.3.21) . (5.3.22)
. (5.3.22) Рис. 10. Пример плоской деформации
Рис. 10. Пример плоской деформации
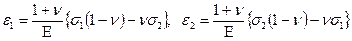 .
. , состоящая при всех t из одних и тех же частиц, граница которых
, состоящая при всех t из одних и тех же частиц, граница которых  непроницаема. При втором подходе – неподвижные объемы
непроницаема. При втором подходе – неподвижные объемы  с проницаемой границей
с проницаемой границей  . Далее будем использовать первый подход.
. Далее будем использовать первый подход. - плотность.
- плотность. , в момент времени t равна
, в момент времени t равна  . Масса объёма
. Масса объёма  . (6.2.1)
. (6.2.1) . (6.2.2)
. (6.2.2)