Усилий в заданном сечении арки с помощью нулевых точек

Расчет 3-х шарнирной арки

Шифр: схема №15, нагрузка №4, размеры № 4

Содержание

Расчет арки на неподвижную нагрузку

1.1. Определение опорных реакций;

1.2. Построение эпюр изгибающих моментов и поперечных сил;

1.3. Определение геометрических параметров в заданном сечении арки;

1.4. Определение внутренних усилий в заданном сечении арки аналитическим способом;

Расчет арки на подвижную нагрузку

2.1. Построение линий влияний опорных реакций и внутренних усилий М, Q, N в заданном сечении аналитическим способом;

2.2.Построение линий влияния внутренних усилий в заданном сечении арки с помощью нулевых точек;

2.3.Определение внутренних усилий в заданном сечении по линиям влияния.

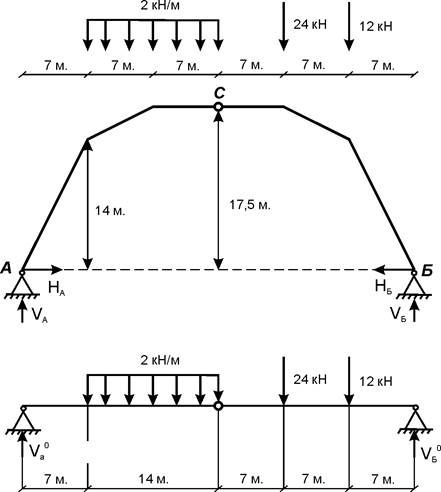
Расчет на неподвижную нагрузку

Определение опорных реакций.

Так как нагрузка действует перпендикулярно линии, соединяющей опоры арки, то арку можно заменить эквивалентной балкой.

Тогда мы можем использовать уравнение равновесия для арки, в которой определим вертикальные составляющие реакций:

∑Ма=0 => Vв=Vв°,

∑Мв=0 => Vа=Vа°,

где Vа° и Vв° - балочные опорные реакции.

Горизонтальные составляющие и распор определим из:

∑Х=0 => На=Нв=Н

Чтобы найти неизвестный распор воспользуемся дополнительным уравнением: алгебраическая сумма моментов сил, действующих на левую или правую половину арки, относительно ключевого шарнира С равна 0.

∑ Мс° =0 => Н=Мс°/f,

где Мс° - балочный момент

∑Ма=0: Vв° = (-2*14*14-24*28-12*35)/42 = 35,33 кН;

∑Мв=0: Vа° = (12*7+24*14+2*14*28)/42 = 28,67 кН;

∑ Мс°(пр) =0: Н = (-24*7-12*14+35,33*21)/17,5 = 23,2 кН.

Построение эпюр изгибающих моментов и поперечных сил

Определение геометрических параметров в заданном сечении

Рассмотрим треугольник авс чтобы определить Yк:

ав=√ас²+вс² = √7²+3,5² = 7,83 м;

cosφ=ас/ав =7/7,83 = 0,89 м;

sinφ=вс/ав = 3,5/7,83 = 0,45 м;

tgφ= sinφ/cosφ = 0,5 м;

d = x*tgφ = 3,5*0,5 = 1,75 м;

Тогда Yк = 14+1,75 = 15,75 м.

Определение внутренних усилий в заданном сечении арки аналитическим способом

Внутренним усилием в заданном сечении является изгибающий момент Мк, поперечная сила Qк (действующая по оси перпендикулярно к оси арки, т.е. по нормали n) и продольные усилия Nк (действующие вдоль оси арки).

Они определяются по методу сечений. Используем готовые формулы Мк, Qк, Nк:

1. Мк = Мк°-Н*Yк,

2. Qк = Qк°cosφк-Hsinφк,

3. Nк = -(Qк*sinφк+H*cosφк),

где Мк° и Qк° - значение момента и поперечной силы в сечении для эквивалентной балки.

Из формулы 1 видно преимущество арки перед балкой, следовательно более экономичная.

Из формулы распора видно, что:

1) Н не зависит от очертаний арки;

2) При f=>0; H=>∞, при f=>∞; H=>0.

Мк° = 28,67*10,5-2*3,5*1,75= 288,79 кНм;

Qк° = 28*67-2*3,5 = 21,67 кН;

Sinφ и cosφ берем из п.1.3 и находим значения Мк, Qк, Nк для данной арки:

Мк = 288,79-23,2*15,75 = -76,61 кНм;

Qк = 19,29-10,44 = 8,85 кН;

Nк = -(9,751+20,648) = -30,399 кН.

Расчет арки на подвижную нагрузку

Построение линий влияний опорных реакций и внутренних усилий М, Q, N в заданном сечении аналитическим способом

Линии влияния вертикальных составляющих Vа и Vв ничем не отличаются от линий влияний вертикающих реакций простой балки того же пролета. Уравнения такие же как для балки типа І.

Vа = Vа° = Р*(l-x)/l = (l-x)/l;

Vв = Vв° =x/l;

Линия влияния горизонтального распора Н строится из формулы Н = Мс°/f, т.е. она имеет такой же вид как линия влияния балочного момента в сечении С, умноженного на коэффициент 1*f, где f- стрела подъема арки.

Построим линии влияния для Мк, Qк, Nк аналитическим способом по известным нам формулам:

Мк = Мк° - Н*Yк,

Qк = Qк°cosφк - Hsinφк,

Nк = -(Qк*sinφк + H*cosφк),

В соответствии с ними линии влияния получаются путем предварительного построения линий влияния изгибающего момента Мк°, поперечной силы Qк° в сечении К для простой балки (тип І) и построения линии влияния распора Н арки. А затем путем сложения их с учетом поправочного коэффциента.

Последовательность построений показано на графике:

2.2.Построение линий влияния внутренних

усилий в заданном сечении арки с помощью нулевых точек

Нулевые точки – точки, в которых ординаты л/в равны нулю. Они образуются при пересечении средней прямой на линиях влияния с осью абсцисс. Чтобы их определить нужно найти такое положение силы Р=1, при котором М_К=0, Q_К=0, N_К=0.

Для построения линий влияния изгибающего момента в сечении К найдем такое положение единичной силы, при котором момент в этом сечении будет равен 0. Для этого используем известное из теоретической механики свойство: система 3-х сил может быть уравновешена в одной точке. Очевидно, что МК=0, если линия действия реакции VA проходит через сечение С с другой стороны, момент в ключевом шарнире МС=0, если линия действия реакции VB проходит через этот шарнир.

Из условия равновесия системы схождения сил следует, что единичная сила должна быть приложена в точке пересечения линии действия V_A и V_B. Эта точка будет нулевой для М_К.

Чтобы определить нулевую точку поперечной силы QK проведем из опоры А прямую, параллельную касательной К оси арки в сечении К до пересечения с (ВС). Получим точку Oq. Если груз Р приложить в эту точку, то QK=0, так как слева от сечения действует лишь одна RA по оси, перпендикулярной действию QK.

Для определения нулевой точки продольной силы проанализируем ее выражение. Из него видно, что N всегда отрицательна, независимо от места сечения, то есть точка, в которой может произойти изменение знака N должна находиться за пределами арки. Чтобы построить эту «мнимую» нулевую точку O_N нужно, чтобы R_A была перпендикулярна N, то есть провести из шарнира А прямую, перпендикулярную касательной к сечению до пересечения с (ВС).

Определив заранее все нулевые точки O_M, O_Q, O_N, можно не производить графическое суммирование составляющих линий влияния, а строить их сруазу с ординатами, отложенными от оси абсцисс. Такой прием построения линий влияния называется способом нулевой точки.

Не нашли, что искали? Воспользуйтесь поиском по сайту: