|
Момент силы относительно произвольного центра, оси.
 При рассмотрении пространственной системы сил в определение момента силы относительно точки должны входить величина момента и направление перпендикуляра к плоскости, содержащей линию действия силы и центр момента. Отсюда вытекает следующее определение момента силы: При рассмотрении пространственной системы сил в определение момента силы относительно точки должны входить величина момента и направление перпендикуляра к плоскости, содержащей линию действия силы и центр момента. Отсюда вытекает следующее определение момента силы:
 (1.1) (1.1)

| | Рис 4
| Величина (модуль) момента равен  , где α - угол между векторами , где α - угол между векторами  и и  . По численной величине момент силы относительно точки равен удвоенной площади треугольника, построенного на силе как на основании и на центре момента как на вершине (рис 3). Вместо удвоенной площади треугольника можно взять площадь параллелограмма со сторонами, равными силе и отрезку . По численной величине момент силы относительно точки равен удвоенной площади треугольника, построенного на силе как на основании и на центре момента как на вершине (рис 3). Вместо удвоенной площади треугольника можно взять площадь параллелограмма со сторонами, равными силе и отрезку  , соединяющему центр моментов с точкой приложения силы. Если сила не равна нулю, то момент может обратиться в нуль только тогда, когда линия действия силы проходит через центр момента. Итак, момент силы относительно некоторого центра равен векторному произведению вектор-радиуса точки приложения силы и вектора силы. Точка приложения силы , соединяющему центр моментов с точкой приложения силы. Если сила не равна нулю, то момент может обратиться в нуль только тогда, когда линия действия силы проходит через центр момента. Итак, момент силы относительно некоторого центра равен векторному произведению вектор-радиуса точки приложения силы и вектора силы. Точка приложения силы  в данном случае не играет никакой роли (рис 4). Действительно, если вектор в данном случае не играет никакой роли (рис 4). Действительно, если вектор  приложен в точке В на той же прямой, то приложен в точке В на той же прямой, то

и

так как векторное произведение  . Понятие момента свободного вектора лишено всякого смысла. Заметим, что . Понятие момента свободного вектора лишено всякого смысла. Заметим, что  , где H-кратчайшее расстояние от линии действия силы до выбранной точки О (его часто называют, и не без основания, плечом силы). Тогда можно дать ещё одно определение момента силы. Моментом силы относительно точки назовем вектор, равный по величине произведению силы на кратчайшее расстояние линии действия ее до точки и направленный по перпендикуляру к плоскости, содержащей силу и точку, в ту сторону, откуда, вращение тела силой представляется происходящим против хода часовой стрелки. , где H-кратчайшее расстояние от линии действия силы до выбранной точки О (его часто называют, и не без основания, плечом силы). Тогда можно дать ещё одно определение момента силы. Моментом силы относительно точки назовем вектор, равный по величине произведению силы на кратчайшее расстояние линии действия ее до точки и направленный по перпендикуляру к плоскости, содержащей силу и точку, в ту сторону, откуда, вращение тела силой представляется происходящим против хода часовой стрелки.

| | Рис 5
| Обратимся теперь к определению момента силы относительно оси (рис 5). Спроектируем силу  на плоскость П, перпендикулярную к этой оси (отрезок ab), и возьмем момент проекции силы на плоскость П, перпендикулярную к этой оси (отрезок ab), и возьмем момент проекции силы  относительно точки О (пересечения, для определённости, оси OZ с плоскостью П). Момент силы относительно точки О (пересечения, для определённости, оси OZ с плоскостью П). Момент силы  численно равен удвоенной площади ОАВ. Алгебраическую величину равную произведению проекции на плоскость, перпендикулярную оси и кратчайшего расстояния от линии действия проекции силы до точки пересечения оси и плоскости назовем моментом силы относительно оси, знак будем определять в зависимости от направления вращения силы численно равен удвоенной площади ОАВ. Алгебраическую величину равную произведению проекции на плоскость, перпендикулярную оси и кратчайшего расстояния от линии действия проекции силы до точки пересечения оси и плоскости назовем моментом силы относительно оси, знак будем определять в зависимости от направления вращения силы  : со знаком плюс, если для наблюдателя, смотрящего на плоскость с конца оси, вращение проекции силы вокруг точки представится совершающимся против часовой стрелки, и со знаком минус в противоположном случае. Из определения момента силы относительно оси следует, что он может быть равным нулю в двух случаях: : со знаком плюс, если для наблюдателя, смотрящего на плоскость с конца оси, вращение проекции силы вокруг точки представится совершающимся против часовой стрелки, и со знаком минус в противоположном случае. Из определения момента силы относительно оси следует, что он может быть равным нулю в двух случаях:
1) если линия действия силы пересекается с осью и
2) если линия действия силы параллельна оси, т.е.- если сила и ось лежат в одной плоскости.
Приняв указанное определение момента силы относительно оси, легко показать, что проекция вектора момента силы относительно некоторой точки на ось, проходящую через точку, равна моменту силы относительно этой оси.
Для доказательства заметим, что модуль вектора момента  силы силы  относительно точки О (рис.5) равен двум площадям треугольника ОАВ - относительно точки О (рис.5) равен двум площадям треугольника ОАВ -  , а момент силы относительно оси ОZ равен, по определению, двум площадям треугольника Оав - , а момент силы относительно оси ОZ равен, по определению, двум площадям треугольника Оав -  , но , но 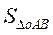 cosα= cosα=  , так как угол α между вектором , так как угол α между вектором  и осью ОZ равен углу между плоскостью перпендикулярной вектору момента силы и плоскостью П, а площадь и осью ОZ равен углу между плоскостью перпендикулярной вектору момента силы и плоскостью П, а площадь  есть проекция площади есть проекция площади  ; следовательно ; следовательно  , что и требовалось доказать. Полученный результат позволяет, там, где необходимо, считать момент силы относительно оси и не считать проекцию вектора момента силы на ось. , что и требовалось доказать. Полученный результат позволяет, там, где необходимо, считать момент силы относительно оси и не считать проекцию вектора момента силы на ось.
Пара сил и её свойства.
Рассмотрим две силы  и и  , равные по величине и направленные в противоположные стороны, но действующие на тело не по одной прямой (рис. 6). Сумма этих двух сил равна нулю, а момент? , равные по величине и направленные в противоположные стороны, но действующие на тело не по одной прямой (рис. 6). Сумма этих двух сил равна нулю, а момент?

или  . Момент таких двух сил не зависит от выбранного центра, то есть вектор . Момент таких двух сил не зависит от выбранного центра, то есть вектор  является свободным: его можно переносить как угодно в пространстве, не изменяя его величины и направления. Кратчайшее расстояние между линиями действия сил h называют плечом пары сил. Численно момент пары равен является свободным: его можно переносить как угодно в пространстве, не изменяя его величины и направления. Кратчайшее расстояние между линиями действия сил h называют плечом пары сил. Численно момент пары равен
 (1.2) (1.2)
Перечислим основные свойства пары сил как свободного вектора:
Пару сил можно переносить в плоскости действия, пару сил можно переносить в плоскость параллельной исходной. Из формулы (1.2) следует, что, оставляя неизменным один из сомножителей, можно менять два остальные, сохраняя при этом значение момента пары: так, например, оставляя неизменным угол α, можно пропорционально изменить величины АВ и F. Совокупность пар, как угодно расположенных в пространстве, статически эквивалентна одной паре с моментом, равным векторной сумме моментов слагаемых пар. Это обозначает: чтобы сложить моменты нескольких пар надо сложить векторно их моменты или по правилу параллелограмма или векторного многоугольника.

| | Рис 6.
| Здесь следует отметить, что, если две пары имеют одинаковый момент, нельзя говорить, что они равны, их действие на тело статически эквивалентно. Пара сил, вообще говоря, является искусственным элементом, так как подобрать равными и параллельными две силы можно только с точностью измеряющих эти величины приборов, но введение её будет полезно при дальнейшем изложении материала.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , где α - угол между векторами
, где α - угол между векторами  и
и  . По численной величине момент силы относительно точки равен удвоенной площади треугольника, построенного на силе как на основании и на центре момента как на вершине (рис 3). Вместо удвоенной площади треугольника можно взять площадь параллелограмма со сторонами, равными силе и отрезку
. По численной величине момент силы относительно точки равен удвоенной площади треугольника, построенного на силе как на основании и на центре момента как на вершине (рис 3). Вместо удвоенной площади треугольника можно взять площадь параллелограмма со сторонами, равными силе и отрезку  , соединяющему центр моментов с точкой приложения силы. Если сила не равна нулю, то момент может обратиться в нуль только тогда, когда линия действия силы проходит через центр момента. Итак, момент силы относительно некоторого центра равен векторному произведению вектор-радиуса точки приложения силы и вектора силы. Точка приложения силы
, соединяющему центр моментов с точкой приложения силы. Если сила не равна нулю, то момент может обратиться в нуль только тогда, когда линия действия силы проходит через центр момента. Итак, момент силы относительно некоторого центра равен векторному произведению вектор-радиуса точки приложения силы и вектора силы. Точка приложения силы  в данном случае не играет никакой роли (рис 4). Действительно, если вектор
в данном случае не играет никакой роли (рис 4). Действительно, если вектор  приложен в точке В на той же прямой, то
приложен в точке В на той же прямой, то

 При рассмотрении пространственной системы сил в определение момента силы относительно точки должны входить величина момента и направление перпендикуляра к плоскости, содержащей линию действия силы и центр момента. Отсюда вытекает следующее определение момента силы:
При рассмотрении пространственной системы сил в определение момента силы относительно точки должны входить величина момента и направление перпендикуляра к плоскости, содержащей линию действия силы и центр момента. Отсюда вытекает следующее определение момента силы: (1.1)
(1.1)


 . Понятие момента свободного вектора лишено всякого смысла. Заметим, что
. Понятие момента свободного вектора лишено всякого смысла. Заметим, что  , где H-кратчайшее расстояние от линии действия силы до выбранной точки О (его часто называют, и не без основания, плечом силы). Тогда можно дать ещё одно определение момента силы. Моментом силы относительно точки назовем вектор, равный по величине произведению силы на кратчайшее расстояние линии действия ее до точки и направленный по перпендикуляру к плоскости, содержащей силу и точку, в ту сторону, откуда, вращение тела силой представляется происходящим против хода часовой стрелки.
, где H-кратчайшее расстояние от линии действия силы до выбранной точки О (его часто называют, и не без основания, плечом силы). Тогда можно дать ещё одно определение момента силы. Моментом силы относительно точки назовем вектор, равный по величине произведению силы на кратчайшее расстояние линии действия ее до точки и направленный по перпендикуляру к плоскости, содержащей силу и точку, в ту сторону, откуда, вращение тела силой представляется происходящим против хода часовой стрелки.
 численно равен удвоенной площади ОАВ. Алгебраическую величину равную произведению проекции на плоскость, перпендикулярную оси и кратчайшего расстояния от линии действия проекции силы до точки пересечения оси и плоскости назовем моментом силы относительно оси, знак будем определять в зависимости от направления вращения силы
численно равен удвоенной площади ОАВ. Алгебраическую величину равную произведению проекции на плоскость, перпендикулярную оси и кратчайшего расстояния от линии действия проекции силы до точки пересечения оси и плоскости назовем моментом силы относительно оси, знак будем определять в зависимости от направления вращения силы  : со знаком плюс, если для наблюдателя, смотрящего на плоскость с конца оси, вращение проекции силы вокруг точки представится совершающимся против часовой стрелки, и со знаком минус в противоположном случае. Из определения момента силы относительно оси следует, что он может быть равным нулю в двух случаях:
: со знаком плюс, если для наблюдателя, смотрящего на плоскость с конца оси, вращение проекции силы вокруг точки представится совершающимся против часовой стрелки, и со знаком минус в противоположном случае. Из определения момента силы относительно оси следует, что он может быть равным нулю в двух случаях: силы
силы  относительно точки О (рис.5) равен двум площадям треугольника ОАВ -
относительно точки О (рис.5) равен двум площадям треугольника ОАВ -  , а момент силы относительно оси ОZ равен, по определению, двум площадям треугольника Оав -
, а момент силы относительно оси ОZ равен, по определению, двум площадям треугольника Оав -  , но
, но 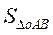 cosα=
cosα=  , так как угол α между вектором
, так как угол α между вектором  есть проекция площади
есть проекция площади  , что и требовалось доказать. Полученный результат позволяет, там, где необходимо, считать момент силы относительно оси и не считать проекцию вектора момента силы на ось.
, что и требовалось доказать. Полученный результат позволяет, там, где необходимо, считать момент силы относительно оси и не считать проекцию вектора момента силы на ось. и
и  , равные по величине и направленные в противоположные стороны, но действующие на тело не по одной прямой (рис. 6). Сумма этих двух сил равна нулю, а момент?
, равные по величине и направленные в противоположные стороны, но действующие на тело не по одной прямой (рис. 6). Сумма этих двух сил равна нулю, а момент? . Момент таких двух сил не зависит от выбранного центра, то есть вектор
. Момент таких двух сил не зависит от выбранного центра, то есть вектор  является свободным: его можно переносить как угодно в пространстве, не изменяя его величины и направления. Кратчайшее расстояние между линиями действия сил h называют плечом пары сил. Численно момент пары равен
является свободным: его можно переносить как угодно в пространстве, не изменяя его величины и направления. Кратчайшее расстояние между линиями действия сил h называют плечом пары сил. Численно момент пары равен (1.2)
(1.2)