
|
|
Признак сравнения отношенийТакже признак сравнения можно сформулировать в более удобной форме — в виде отношений. Формулировка
Доказательство Перемножая неравенства, составленные для
Дальше достаточно применить признак сравнения для положительных рядов
Предельный признак сравнения Поскольку достоверно установить справедливость этого неравенства при любых n — довольно сложная задача, то на практике признак сравнения обычно используется в предельной форме. Формулировка
Доказательство Если
Из ограниченности частных сумм 20 При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г. Если для числового ряда
существует такое число
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то ряд расходится. Признак сходимости д’Аламбера в предельной форме Если существует предел то рассматриваемый ряд абсолютно сходится если Замечание. Если Доказательство 1. 2. Примеры Ряд
абсолютно сходится для всех комплексных
Ряд
расходится при всех
Если
удовлетворяют этому условию, причём первый ряд (гармонический) расходится, а второй сходится. 21 Радикальный признак Коши — признак сходимости числового ряда: Если для числового ряда
с неотрицательными членами существует такое число Предельная форма Условие радикального признака равносильно следующему:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Доказательство 1. Пусть
Раскрыв модуль, получаем:
Поскольку 2. Пусть
Раскрыв модуль, получаем:
Поскольку Примеры Ряд
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
Рассмотрим ряд
22 Интегральный признак Коши́ – Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши – Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на
Формулировка теоремы
Набросок доказательства
1. Построим на графике f(x) ступенчатые фигуры как показано на рисунке 2. Площадь большей фигуры равна 3. Площадь меньшей фигуры равна 4. Площадь криволинейной трапеции под графиком функции равна 5. Получаем 6. Далее доказывается с помощью критерия сходимости знакоположительных рядов. Примеры · ·
23 Гармонический ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:
Ряд назван гармоническим, так как складывается из «гармоник»: 25 Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
Признак Лейбница Основная статья: Теорема Лейбница о сходимости знакочередующихся рядов Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Замечания: Если, выполнены все условия, и ряд из модулей ( Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым. Пример
Теперь воспользуемся признаком Лейбница: 1. знакочередование выполнено 2. 3. Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 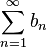 , начиная с некоторого места (
, начиная с некоторого места (  ), выполняется неравенство:
), выполняется неравенство:
 ,
то из сходимости ряда
,
то из сходимости ряда  , получаем
, получаем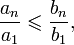 или
или 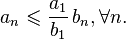
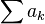 и
и 
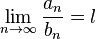 ,
то при
,
то при 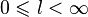 из сходимости
из сходимости  из расходимости
из расходимости  то для достаточно больших
то для достаточно больших 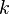
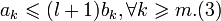
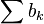 следует ограниченность частных сумм
следует ограниченность частных сумм 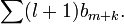 Соотношения
Соотношения  обеспечивают на основании признака сравнения сходимость
обеспечивают на основании признака сравнения сходимость  и вместе с тем сходимость
и вместе с тем сходимость  Если же
Если же  то
то 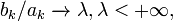 и
и 

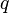 ,
, 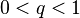 , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство


 , а если
, а если  — расходится.
— расходится. , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.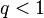 , тогда существует
, тогда существует 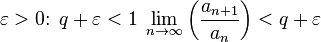 , существует
, существует  , для любого
, для любого  .
.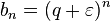 сходится (как геометрическая прогрессия). Значит, ряд из
сходится (как геометрическая прогрессия). Значит, ряд из 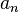 сходится (по признаку сравнения).
сходится (по признаку сравнения).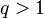 , тогда существует
, тогда существует 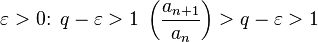 .
.  для любого
для любого  . Тогда
. Тогда 
 , так как
, так как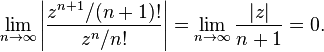
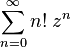
 , так как
, так как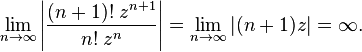
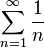 и
и 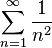
 ,
, 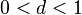 , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
, то данный ряд сходится.
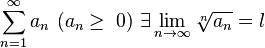 , то
если
, то
если 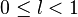 ряд сходится,
если
ряд сходится,
если 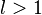 ряд расходится,
если
ряд расходится,
если 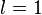 вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.
 . Очевидно, что существует такое
. Очевидно, что существует такое  , что
, что  . Поскольку существует предел
. Поскольку существует предел 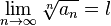 , то, подставив в определение предела выбранное
, то, подставив в определение предела выбранное  , получим:
, получим:



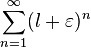 сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 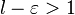 . Поскольку существует предел
. Поскольку существует предел  расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 


 ряд сходится.
ряд сходится. , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде. (функция принимает неотрицательные значения)
2.
(функция принимает неотрицательные значения)
2. 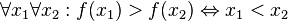 (функция монотонно убывает)
3.
(функция монотонно убывает)
3.  (соответствие функции члену ряда)
Тогда ряд
(соответствие функции члену ряда)
Тогда ряд  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.



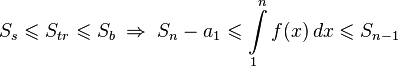
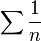 расходится так как
расходится так как  .
. сходится так как
сходится так как  .
.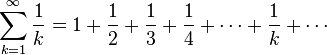 .
. от длины исходной струны[1].
от длины исходной струны[1].
 (монотонное убывание {an})
2.
(монотонное убывание {an})
2.  .
Тогда этот ряд сходится.
.
Тогда этот ряд сходится.
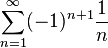 . Ряд из модулей имеет вид
. Ряд из модулей имеет вид 
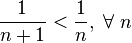
 .
.