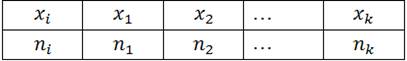|
|
Математическое ожидание абсолютно непрерывного распределения§ Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётсяплотностью
Математическое ожидание случайного вектора Пусть
то есть математическое ожидание вектора определяется покомпонентно. Математическое ожидание преобразования случайной величины Пусть
если
если Если распределение
В специальном случае, когда Простейшие свойства математического ожидания § Математическое ожидание линейно, то есть § Математическое ожидание сохраняет неравенства, то есть если если
§ Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если
§ Математическое ожидание произведения двух независимых случайных величин
Дополнительные свойства математического ожидания § Неравенство Маркова; § Теорема Леви о монотонной сходимости; § Теорема Лебега о мажорируемой сходимости; § Лемма Фату.kl;;l; Примеры § Пусть случайная величина имеет дискретное равномерное распределение, то есть
равно среднему арифметическому всех принимаемых значений. § Пусть случайная величина имеет непрерывное равномерное распределение на интервале
§ Пусть случайная величина
то есть математическое ожидание
12)Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. Обозначается Определение Пусть
где символ РЕКЛАМА Замечания § В силу линейности математического ожидания справедлива формула:
§ Дисперсия является вторым центральным моментом случайной величины; § Дисперсия может быть бесконечной. См., например, распределение Коши. Свойства дисперсииДисперсия любой случайной величины неотрицательна: § Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; § Если случайная величина равна константе, то её дисперсия равна нулю: § Пусть
где В частности: § если § § § Пример Пусть случайная величина
Тогда
и
Тогда
Определение 2. Среднеквадратичным отклонением случайной величины называется корень квадратный из еедисперсии:
или в развернутом виде
Среднеквадратичное отклонение обозначают также Замечание 1. При вычислении дисперсии формулу (1) бывает удобно преобразовать так:
Итак,
т. е. дисперсия равна разности математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины. Пример 1. Производится один выстрел по объекту. Вероятность попадания Решение. Строим таблицу значений числа попаданий
Чтобы представить смысл понятия дисперсии и среднеквадратичного отклонения как характеристики рассеивания случайной величины, рассмотрим примеры. 14) Множество социальных объектов, явлений, процессов, которые являются предметом изучения социологического исследования, образуют генеральную совокупность. Любую генеральную совокупность характеризует некоторый явно задаваемый признак (или набор признаков), по значению которого всегда можно однозначно определить, относится данный объект к генеральной совокупности или нет. Часть объектов генеральной совокупности, выступающих в качестве объектов наблюдения, называется выборочной совокупностью. Иными словами, если генеральная совокупность включает все без исключения единицы, составляющие объект исследования, то выборочная совокупность представляет собой специальным образом отобранную часть генеральной совокупности. Выборочная совокупность конструируется таким образом, чтобы при минимуме исследуемых объектов удавалось с необходимой степенью гарантии представить всю генеральную совокупность. Единицей отбора называют элементы генеральной совокупности, которые выступают единицами счета в различных процедурах отбора, формирующих выборку. Единицами наблюдения называют элементы сформированной выборочной совокупности, которые непосредственно подвергаются исследованию. Единица отбора и единица наблюдения представляют собой социальные объекты, обладающие характеристиками, существенными для предмета конкретного социологического исследования. Они могут совпадать (в простых схемах отбора) и различаться (при сложных комбинированных схемах отбора). Единицами отбора могут выступать как отдельные индивиды, так и целые коллективы или целые группы (например, при проведении сплошного опроса). При совпадении единицы наблюдения с единицей отбора применяется одноступенчатая (простая) выборка, при несовпадении – многоступенчатая (сложная) выборка.
Объем выборки зависит от ряда факторов: · от цели и задач исследования, · от степени однородности генеральной совокупности, · от величины доверительной вероятности, · от точности результатов (величины допускаемой ошибки репрезентативности Различаются выборки вероятностные и целенаправленные. Модель вероятностной (случайной) выборки связана с понятием вероятности, широко используемым во многих социальных науках. В самом общем случае вероятность некоторого ожидаемого события есть отношение числа всех возможных событий к числу ожидаемых. При этом общее число событий должно быть достаточно большим (статистически значимым). Кроме этого, необходимо создать условия равновероятности отбора единиц. Условие равновероятности должно гарантировать для каждого элемента генеральной совокупности попасть в выборочную. Такая ситуация возможна при равномерном распределении элементов генеральной совокупности. Существуют различные методы вероятностной (случайной) выборки: · метод собственно-случайного отбора, · случайно-бесповторный метод, · случайно-повторный, · метод механической выборки (например, каждый десятый элемент генеральной совокупности включается в выборочную).
Нередко используется довольно точный метод отбора выборочной совокупности - метод серийной выборки. Суть этого метода заключается в расчленении генеральной совокупности на однородные части (серии) по заданному признаку. После этого отбор респондентов осуществляетсяв каждой серии по заданному признаку. Кроме этого, существует метод гнездовой выборки. «Гнездо» представляет собой группу каких-либо объектов, состоящих из ряда элементов. В качестве единиц исследования используют не отдельных респондентов, а группы, коллективы.
Наряду с вероятностной выборкой в социологических исследованиях применяется также и целенаправленная выборка. Целенаправленная выборка осуществляется не с помощью теории вероятности, а при использовании ряда методов: · стихийной выборки, · основного массива, · квотной выборки.
Стихийная выборка чаще всего применяется в журналистике. Примером стихийной выборки может служить почтовый опрос. Достоверность и качество полученной при этом информации очень низкие и распространяются только на опрошенную совокупность. Метод основного массива применяется как «зондаж» при проведении пилотажного исследования, при этом изучается 60-70% генеральной совокупности. Наиболее точным из методов целенаправленных выборок можно считать метод квотной выборки. Однако, применение этого метода возможно при наличии статистических данных о генеральной совокупности. Все данные о признаках генеральной совокупности выступают в качестве квот, а отдельные числовые значения – в качестве параметров квот. При квотной выборке респонденты отбираются целенаправленно с соблюдением параметров квот. В качестве квоты могут выступать не более четырех признаков. Например, пол, возраст, стаж работы, уровень образования и т.д.
Определение объема и вида выборки - недостаточное условие правомерности распространения выводов исследования на всю генеральную совокупность. Из всего многообразия возможных выборочных совокупностей необходимо отобрать одну, наиболее точную. Способность выборки отражать, моделировать значимые свойства генеральной совокупности – есть репрезентативностьвыборки. Отклонение результатов выборочного исследования от существенных характеристик генеральной совокупности называется ошибкой репрезентативности. Ошибки репрезентативности могут быть случайными и систематическими. Случайныеошибки репрезентативности носят вероятностный характер и при повторном измерении изменяются по вероятностным законам. Систематическими ошибками репрезентативности называют ошибки смещения, нарушающие точность выборочной совокупности. Систематические ошибки возникают при просчетах на стадии проектирования выборки, при отсутствии информации о социальном объекте, при неправильном выборочном отборе. Систематические ошибки репрезентативности могут быть также непреднамеренными (например, просчет на стадии проектирования выборки) и преднамеренными (обусловленными идеологическими, экономическими и т.д. факторами).
15) Дискретный вариационный ряд
Вариационный ряд может быть дискретным (выборка значений дискретной случайной величины) и непрерывным (интервальным) (выборка значений непрерывной случайной величины). Дискретный вариационный ряд имеет вид: Выборка (выборочная совокупность) – совокупность наблюдений, отобранных случайным образом из генеральной совокупности. Число наблюдений в совокупности называется ее объемом. N – объем генеральной совокупности. n– объем выборки(сумма всех частот ряда). Частотой варианты хi называется число ni (i=1,…,k), показывающее, сколько раз эта варианта встречается в выборке. Частостью (относительной частотой, долей) варианты хi (i=1,…,k) называется отношение ее частоты ni к объему выборки n. Ранжирование опытных данных - операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания. Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов хi с соответствующими им частотами или частностями. По данным дискретного вариационного ряда строят полигон частот или относительных частот. Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот. Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2), ..., (xk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты Wi. Точки ( xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
xi – варианты дискретного ряда ni – частоты вариант wi– частости вариант(относительная частота)
Интервальным вариационным рядом называют упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины. Для построения интервального ряда необходимо: 1. определить величину частичных интервалов; 2. определить ширину интервалов; 3. установить для каждого интервала его верхнюю и нижнюю границы; 4. сгруппировать результаты наблюдении. 1. Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном случае исходя из целей исследования, объема выборки и степени варьирования признака в выборке. Приблизительно число интервалов k можно оценить исходя только из объема выборки n одним из следующих способов:
2. Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов h вычисляют:
где xmax и xmin - максимальная и минимальная варианты выборки;
3. Нижняя граница первого интервала xh1 выбирается так, чтобы минимальная варианта выборки xmin попадала примерно в середину этого интервала: xh1 = xmin - 0,5·h . Промежуточные интервалы получают прибавляя к концу предыдущего интервала длину частичного интервала h: xhi = xhi-1 +h . Построение шкалы интервалов на основе вычисления границ интервалов продолжается до тех пор, пока величина xhi удовлетворяет соотношению: xhi < xmax + 0,5·h . 4. В соответствии со шкалой интервалов производится группирование значений признака - для каждого частичного интервала вычисляется сумма частот ni вариант, попавших в i-й интервал. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы интервала. 16)Точечные и интервальные оценки. Оценки неизвестных параметров бывают двух видов - ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ.
X = (x1+x2+...+xn)/n, где: X - среднее арифметическое (точечная оценка МО); Вычисление интервальной оценки рассмотрим на примере интервальной оценки МО для случайной величины подчиняющейся нормальному закону распределения. Границы доверительного интервала определятся по формулам: Xmin = X - T(ν,P)*S/(n)1/2
Xmax = X + T(ν,P)*S/(n)1/2
где: Xmin, Xmax - нижняя и верхняя границы интервала; S = [(x1 - X)2 + (x2 - X)2 + ... + (xn - X)2]1/2 - корень квадратный из оценки дисперсии случайной величины X ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ СТАТИСТИКИ - число независимых случайных величин, по которым вычисляется данная статистика. Например, при вычислении среднего арифметического все случайные величины в выборкеx1,x2,...,xn независят друг от друга. В оценке S из n отклонений вида (xi - X)2 независимы только n-1 (т.к. в формуле присутствует X, то по любому набору n-1 отклонений вычисляется n-ое). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , равно
, равно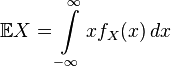 .
.
 - случайный вектор. Тогда по определению
- случайный вектор. Тогда по определению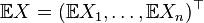 ,
,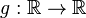 борелевская функция, такая что случайная величина
борелевская функция, такая что случайная величина  имеет конечное математическое ожидание. Тогда для него справедлива формула:
имеет конечное математическое ожидание. Тогда для него справедлива формула: ,
, имеет дискретное распределение;
имеет дискретное распределение; ,
, случайной величины
случайной величины  .
. , Математическое ожидание
, Математическое ожидание  называется k-тым моментом случайной величины.
называется k-тым моментом случайной величины.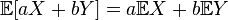 ,
, — случайные величины с конечным математическим ожиданием, а
— случайные величины с конечным математическим ожиданием, а  — произвольные константы;
— произвольные константы; почти наверное, и
почти наверное, и  — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины
— случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины  ;
; почти наверное, то
почти наверное, то .
. .
. Тогда её математическое ожидание
Тогда её математическое ожидание
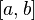 , где
, где  . Тогда её плотность имеет вид
. Тогда её плотность имеет вид 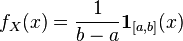 и математическое ожидание равно
и математическое ожидание равно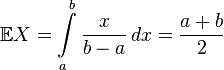 .
. ,
, в русской литературе и
в русской литературе и 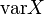 (Шаблон:Lang-en) в зарубежной. В статистике часто употребляется обозначение
(Шаблон:Lang-en) в зарубежной. В статистике часто употребляется обозначение 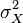 или
или  . Квадратный корень из дисперсии
. Квадратный корень из дисперсии  называетсясреднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.
называетсясреднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.
 обозначает математическое ожидание.
обозначает математическое ожидание.
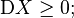
 Верно и обратное: если
Верно и обратное: если  , то
, то  п.н.
п.н. — случайные величины, а
— случайные величины, а  — их произвольная линейная комбинация. Тогда
— их произвольная линейная комбинация. Тогда
 — ковариация случайных величин
— ковариация случайных величин 
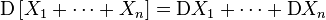 ,
,


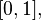 т. е. еёплотность вероятности задана равенством
т. е. еёплотность вероятности задана равенством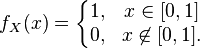






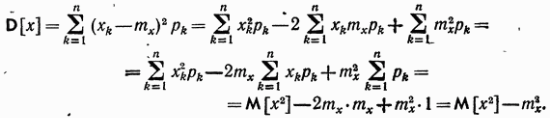

 . Определитьматематическое ожидание, дисперсию и среднеквадратичное отклонение.
. Определитьматематическое ожидание, дисперсию и среднеквадратичное отклонение.
 Следовательно,
Следовательно,