
|
|
Понятие определенного интеграла, его геометрический12 Пример 7.1. Функция F(x)= x2является первообразной для функции f(x)= 2x на всей числовой оси, так для любого x выполняется Функция F(x)= sinx является первообразной для f(x)= cosx, т. к.
Из примеров видно, что если задана функция f(x) , то ее первообразная не может быть определена однозначно, т. е. f(x) имеет не одну первообразную. Теорема. Пусть функция F(x) является первообразной для f(x). Тогда и функция F(x)+ C, в которой С — постоянная величина, также является первообразной для f(x). Обратно, если F1(x) и F2(x) — две различные первообразные для f(x), то они отличаются на постоянную величину С, т. е. F1(x) = F2(x) + C. Доказательство: а) так как
то по определению первообразной функции F(x) + C является первообразной для f(x); б) пусть у функции f(x) существуют две первообразные F1(x)и F2(x). Найдем их разность, которая тоже является функцией Ф(x) = F1(x) – F2(x). Найдем ее производную.
Так как производная функции Ф(х) равна нулю, то Ф(х) представляет собой некоторую постоянную величину С. Поэтому Ф(х) = С, F1(x) – F2(x) = C
Совокупностьвсех первообразных для функции f(x) называется неопределенным интегралом от f(x) в области определения первообразных. Неопределенный интеграл обозначается
где Так как все первообразные для f (x) отличаются друг от друга на постоянную величину, то ясно, что
т. е. неопределенный интеграл определяет семейство функций. Процесс нахождения неопределенного интеграла от функции f(x) называется интегрированием этой функции. Для нахождения конкретной первообразной необходимо задать координаты точки, через которую будет проходить график первообразной. Свойства неопределенного интеграла. 1. Производная от неопределенного интеграла равна подынтегральной функции
Действительно,
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
По определению дифференциала
3. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная
Так как было определено, что
4. Постоянный множитель можно вынести за знак интеграла
Доказательство:
5. Интеграл от алгебраической суммы конечного числа функций равен соответствующей алгебраической сумме интегралов от этих функций
Рассмотрим интегралы от основных элементарных функций в виде таблицы, которая получается путем простого подбора первообразной так, чтобы производная первообразной была бы равна подынтегральной функции. Таблица неопределенных интегралов 1. 2. 3. 4. 5. 6.
8. 9. 10.
11. 12.
13. Интегралы, входящие в эту таблицу, обычно называют табличными. Пример 7.2. 1.
2.
3.
4.
5. Нахождение неопределенных интегралов путем обращения к таблице интегралов часто называют непосредственным интегрированием. Методы вычисления неопределенных интегралов Одним из методов нахождения интегралов, отличных от табличных, является преобразование подынтегральной функции таким образом, чтобы осуществить переход от произведения или частного функций к их сумме и, в конечном итоге, на основе свойств интеграла 4 и 5 свести эти интегралы к табличным. Такой метод интегрирования называют методом разложения. Часто при этом успех достигается путем применения формул сокращенного умножения, а также тригонометрических формул перехода от произведения (или степени) к сумме. Пример 7.3.
Пример 7.4.
Пример 7.5.
Пример 7.6.
Пример 7.7.
Пример 7.8.
Метод замены переменной. Если подынтегральное выражение можно представить в виде
а интеграл t = u(x). Тогда
и легко находится выражение для интеграла через переменную интегрирования t. В заключение необходимо выполнить обратную подстановку, вернувшись к переменной x. Такая замена переменной позволяет свести сложный интеграл к табличному. Нахождение Наиболее просто осуществить подстановку, когда u(x) является линейной функцией вида u(x) = kx + b, то есть если интеграл имеет вид
Действительно, пусть F(x) — первообразная для f(x). Тогда
Следовательно,
Пример 7.9. Найти неопределенный интеграл Решение. Используя последнюю формулу, можно сразу записать ответ
Рассмотрим этот пример подробнее, используя выделение дифференциала:
Следовательно, нужно сделать замену переменной (подстановку) u = 3x + 2. Запишем
Пример 7.10.
Обозначим t = cos x. Тогда
Пример 7.11.
Необходимо уточнить, что во многих случаях выделить дифференциал достаточно трудно. Поэтому часто метод замены переменной используют, просто пробуя различные подстановки.
Пример 7.12. Рассмотрим последний пример, в котором использовалась подстановка t = x2 + 5. Тогда
и, подставляя в исходный интеграл, имеем
Существует несколько типовых приемов при интегрировании методом замены переменной. Рассмотрим некоторые из них.
1. Если нужно найти интеграл от алгебраической дроби, причем в знаменателе дроби находится квадратный трехчлен ax2 + bx + c, а в числителе — многочлен от x не выше первой степени, то в знаменателе выделяется полный квадрат и новая переменная приравнивается к выражению, возводимому в квадрат. Тот же прием применяется, если квадратный трехчлен находится под знаком квадратного корня.
2. Если в знаменателе дроби подынтегральной функции находится квадратный трехчлен, а в числителе — многочлен от x степени выше первой, то следует провести деление, например, уголком числителя на знаменатель, после чего интеграл сводится к уже рассмотренным случаям.
3. Если в подынтегральной функции имеются корни различной степени из x, то часто к успеху приводит замена переменной
Пример 7.16. 4. Если подынтегральная функция представляет собой тригонометрическое выражение, то часто используют замену переменной
Найдем dx. Для этого отразим переменную x
И окончательно
Пример 7.17.
Очень часто на практике является полезным использование следующих формул
Пример 7.19.
Интегрирование по частям.В некоторых случаях интеграл можно представить в виде
Если при этом легко вычисляется интеграл
Эта формула легко получается при интегрировании дифференциала произведения двух функций. Действительно,
Интегрируя, получаем
Интегрирование по частям обычно используют тогда, когда подынтегральная функция представляет собой произведение двух функций разного типа (степенной и тригонометрической; степенной и показательной; степенной и логарифмической; тригонометрической и показательной и т. п.). Если в подынтегральном выражении имеется логарифмическая функция, то ее следует принять за u, а если логарифмической функции в подынтегральном выражении нет, то за u принимают степенную функцию. Все, что остается под интегралом, принимают за dv.
Пример 7.21.
Не все интегралы могут быть выражены через элементарные функции. Эти интегралы имеют вид:
Для вычисления таких интегралов (иногда их называют неберущимися) используются специальные методы.
Понятие определенного интеграла, его геометрический
Пусть на отрезке [a, b] определена некоторая функция y = f(x) (рис. 13.1). Разобьем отрезок [a, b] на n частей точками x1 , x2 ,…, xn–1 . Для унификации обозначений положим a = x0 ; b = xn . Отрезок [xk–1 , xk] назовем k-тым частичным отрезком. Длина k-того частичного отрезка равна
Число d равное наибольшей длине k-того частичного отрезка называется диаметром или мелкостью разбиения
Выберем на каждом частичном отрезке [xk–1 , xk] произвольную точку
Функция Если существует предел интегральных сумм при Эту формулу можно записать в виде:
Числа a и b называются соответственно нижними верхним пределами интегрирования, а функция f(x), как и в случае неопределенного интеграла, называется подынтегральной функцией. Отметим, что в отличие от неопределенного интеграла, представляющего собой множество функций, определенный интеграл — это вполне определенное число.
Геометрический смысл определенного интеграла.Как видно из рис. 7.1, интегральная сумма
численно равна площади заштрихованной ступенчатой фигуры.
При переходе к пределу при
Рис. 7.1. Разбиение площади под кривой функции y = f(x)
Следовательно, геометрический смысл определенного интеграла
Рис. 7.2. Геометрический смысл определенного интеграла
Символ абсолютной величины здесь используется потому, что площадь фигуры является величиной положительной, а определенный интеграл может быть отрицательным числом, если, например, f(x) < 0 на отрезке [a, b] или если при положительной f(x) верхний предел интегрирования меньше нижнего.
Экономический смысл определенного интеграла состоит в том, что если подынтегральная функция является предельной величиной (т. е. производной) какого-либо экономического показателя, то определенный интеграл представляет собой соответствующую этому показателю суммарную величину. Например, пусть известна производительность труда как функция времени f(t). Из курса экономики известно, что производительность труда представляет собой предельный объем произведенной продукции (т. е. производную объема произведенной продукции по времени). Тогда объем V продукции, произведенной от момента времени t1 до момента t2, равен определенному интегралу

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Функция F1(x)= x2–3 также первообразная для f(x)= 2x, т. к.
. Функция F1(x)= x2–3 также первообразная для f(x)= 2x, т. к.  .
.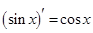 . Но функция F1(x)= sinx + 5 также является первообразной для f(x)= cosx, т. к.
. Но функция F1(x)= sinx + 5 также является первообразной для f(x)= cosx, т. к.  .
.  ,
, .
. F1(x) = F2(x) + C.
F1(x) = F2(x) + C. ,
, — знак интеграла, f(x) — подынтегральная функция, f(x) dx — подынтегральное выражение, а переменная x называется переменной интегрирования.
— знак интеграла, f(x) — подынтегральная функция, f(x) dx — подынтегральное выражение, а переменная x называется переменной интегрирования. ,
, .
. .
. .
. .
. .
. , то
, то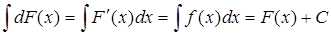 .
. .
.
 .
. .
. ,
,  ;
;
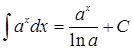 ;
; ;
; ;
; ;
; 7.
7. 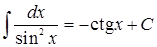 ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. .
. .
. .
.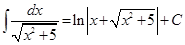 .
. .
. .
.

 .
.


 .
.
 .
.
 .
. ,
, является табличным, то для нахождения интеграла
является табличным, то для нахождения интеграла 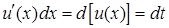
 в подынтегральной функции часто называют выделением дифференциала.
в подынтегральной функции часто называют выделением дифференциала. .
. , d[u(x)]= kdx и
, d[u(x)]= kdx и  .
. .
. .
.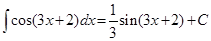 .
. .
.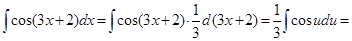
 .
.
 .
. .
.
 .
. В примере использовалось обозначение t = x2 + 5.
В примере использовалось обозначение t = x2 + 5. ;
;  ;
; 
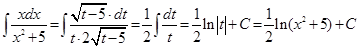 .
.
 Пример 7.13.
Пример 7.13.



 .
. Пример 7.14.
Пример 7.14.

 .
. Пример 7.15.
Пример 7.15.



 .
. , где n — наименьшее общее кратное показателей степени всех корней.
, где n — наименьшее общее кратное показателей степени всех корней.


 .
. . Тогда тригонометрические функции запишутся в виде:
. Тогда тригонометрические функции запишутся в виде: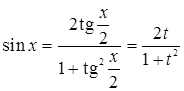 ;
;  ;
; .
.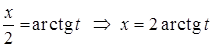 .
. .
. .
. ;
; .
. Пример 7.18.
Пример 7.18.

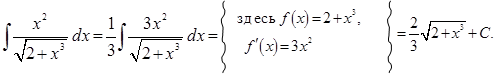
 .
. , то следует воспользоваться формулой, называемой формулой интегрирования по частям
, то следует воспользоваться формулой, называемой формулой интегрирования по частям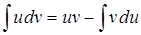 .
. .
. ;
;  .
. Пример 7.20.
Пример 7.20.
 .
.

 .
.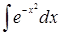 ;
;  ;
; 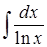 ;
;  ;
;  ;
;  .
. и экономический смысл
и экономический смысл xk = xk – xk–1 .
xk = xk – xk–1 . .
.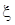 k , найдем f(
k , найдем f(  k) и составим сумму
k) и составим сумму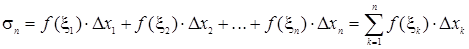 .
. называется интегральной суммой для функции f(x) на отрезке [a, b]. Ясно, что таких интегральных сумм можно составить бесконечное множество.
называется интегральной суммой для функции f(x) на отрезке [a, b]. Ясно, что таких интегральных сумм можно составить бесконечное множество. (при этом
(при этом 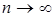 ), то он называется определенным интегралом от функции f(x) в пределах от a до b, а функция f(x) называется интегрируемой на отрезке [a, b].
), то он называется определенным интегралом от функции f(x) в пределах от a до b, а функция f(x) называется интегрируемой на отрезке [a, b].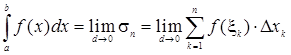 .
.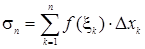
 , а ступенчатая линия, ограничивающая сверху заштрихованные прямоугольники, совпадет с графиком функции y = f(x) на отрезке [a, b].
, а ступенчатая линия, ограничивающая сверху заштрихованные прямоугольники, совпадет с графиком функции y = f(x) на отрезке [a, b].

 .
.