
|
|
Численное интегрирование. Метод трапеций.На частичном отрезке интегрирования Поставляя это выражение в формулу (4.12) и выполняя интегрирование по частичным отрезкам приходим к формуле трапеций: (4)
Название метода связано с тем, что интеграл по отрезку В случае постоянного шага интегрирования формула трапеций принимает вид:
Численное интегрирование. Формула Симпсона. Разобьем интервал интегрирования Интегрируя это выражение на отрезке Приближенное значение интеграла на интервале Полученное соотношение называется формулой Симпсона или формулой парабол. Задача Коши для дифференциального уравнения Для обыкновенного дифференциального уравнения первого порядка задача Коши состоит в следующем: найти решение уравнения
удовлетворяющего начальному условию y(x0)=y0 . (2) Необходимо найти на отрезке [x0,xn] такую непрерывную функцию y = y(x), которая удовлетворяет дифференциальному уравнению (1) и начальному условию (2). Нахождение такого решения называют решением задачи Коши Метод Эйлера Численное решение задачи Коши заключается в следующем. На отрезке [a,b] задается конечное множество точек В выбранных точках xi отыскиваются приближенные значения искомой функции yi ≈ y(xi) . . Для построения рабочей формул метода Эйлера разделим отрезок [a,b] на Приближенные значения искомой функции yi ≈ y(xi) в выбранных точках xi вычисляются последовательно по формуле:
При этом искомая интегральная кривая y(x), проходящая через точку (x0,y0), заменяется ломанной с вершинами в точках (xi,yi). Для практической оценки погрешности метода можно использовать правило Рунге. Для этого прибегают к следующему приему вычисления по формуле(3) проводятся дважды: с шагом h и h/2, что удваивает число n. За оценку погрешности принимается величина Метод Эйлера приводит к систематическому накоплению ошибок, поэтому в практике расчетов используют модификации этого метода: метод ломаных и метод Эйлера-Коши.В первом случае сначала вычисляют промежуточные значения 37) Метод Рунге-Кута На практике широко применяется одношаговый метод четвертого порядка Рунге-Кутта. 38) Метод Адамса Пусть для задачи Коши найдены каким-либо способом (например, методом Эйлера или Рунге-Кутта) три последовательных значения искомой функции, где h – шаг изменения Метод адамса 4 порядка м – Метод исключения.Суть метода состоит в том, что в ходе решения система ДУ сводится к одному дифференциальному уравнению. 1. Метод Эйлера. yij+1=yij+hfi(xi,y1j y2j..ynj) j - номер шага. xj+1=xj+h 2. Модифицированный метод Эйлера. ki1=h*fi(xj,y1j..ynj) ki1=h*fi(xj+h,y1j+ki1..ynj+ki2) yij+1=yij+(ki1+ki2)/2 xj+1=xj+h 3. Метод Рунге-Кутта четвертого порядка. ki1=hfi(xj,y1j..ynj) ki2=hfi(xj+h/2,y2j+ki1/2,..,ynj+kn1/2) ki3=hfi(xj+h/2,y2j+ki2/2,..,ynj+kn2/2) ki4=hfi(xj+h,y1j+ki2,..,ynj+kn3) yij+1=yij+(ki1+2ki2+2ki3+ki4)/6 xj+1=xj+h 40) Методы Рунге-Кутта можно использовать не только для решения дифференциальных уравнений первого порядка но и для решения дифференциальных уравнений более высоких порядков Любое дифференциальное уравнение m-го порядка
можно свести к системе, состоящей из m уравнений первого порядка при помощи замен. В результате дифференциальное уравнение m -го порядка (12.8) сводится к системе, состоящей из m дифференциальных уравнений первого порядка:
Решением системы (12.2), а значит и дифференциального уравнения m -го порядка (12.1) является m табличных функций

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 подынтегральная функция
подынтегральная функция  заменяется интерполяционным полиномом первой степени, т.е. прямой, проходящей через точки
заменяется интерполяционным полиномом первой степени, т.е. прямой, проходящей через точки  и
и  (рис. 4.4):
(рис. 4.4): .
. .
.
 (рис. 4.4).
(рис. 4.4). . (5)
. (5) на четное число n равных отрезков с шагами
на четное число n равных отрезков с шагами  . На каждом отрезке
. На каждом отрезке  , содержащем три узла, заменим подынтегральную функцию интерполяционным полиномом второй степени, т.е. параболой
, содержащем три узла, заменим подынтегральную функцию интерполяционным полиномом второй степени, т.е. параболой

 . (6)
. (6)
 . (7)
. (7) y'=f(x,y), (1)
y'=f(x,y), (1)
 .
. равных частей и вычислим шаг интегрирования
равных частей и вычислим шаг интегрирования  . Сформируем систему равноотстоящих точек
. Сформируем систему равноотстоящих точек  ,
,  , где
, где  ,
,  .
. ,
, 
 , (3)
, (3)
 и находят направление поля интегральных кривых в средней точке
и находят направление поля интегральных кривых в средней точке  , а затем полагают
, а затем полагают  .ф
.ф ,
,  уточняется следующим образом:
уточняется следующим образом: 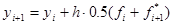



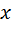 .
. ,
, ,
, ,
, .
. в виде таблицы. Продолжение вычисленный функции из четырех точек осуществляется по экстраполяционной формуле Адамса:
в виде таблицы. Продолжение вычисленный функции из четырех точек осуществляется по экстраполяционной формуле Адамса:  (1.3)
(1.3) . (1.4)
. (1.4)






