|
|
Форматирование линий и маркеров для графика нескольких функцийЕсли строится график нескольких функций, то можно форматировать линии и маркеры каждой кривой отдельно. Выполним следующие команды: » х=-6:.1:6; Рис. 3.11 показывает пример такого форматирования для графика, полученного исполнением этих команд. Кстати, обратите внимание на то, как заданы степени синуса. Записать эти выражения в виде sin(x)^3 и cos(x)^5 будет грубейшей ошибкой, поскольку х здесь вектор. Операторы ^ ??(.^)в данном случае дают поэлементное возведение в степень, что и нужно для построения графиков этих функций.
Рис. 3.11.Пример форматирования для графика трех функций
Форматирование осей графиков Аналогично описанным выше правилам выполняется форматирование и других объектов графиков. Например, указав курсором мыши на оси графиков (на них тоже есть метки в виде черных квадратиков) и дважды щелкнув левой клавишей мыши, можно увидеть появление окна форматирования объектов дескрипторной графики Property Editor (Редактор свойств, Графический редактор свойств) (рис. 3.12), настроенного на форматирование осей.
Рис. 3.12.Пример форматирования осей графика Окно графического редактора свойств дескрипторной графики имеет множество вкладок, настройки которых довольно очевидны, и ничто не мешает читателю поэкспериментировать с ними несколько минут. Это позволит понять простоту и одновременно высокую эффективность средств форматирования объектов графики. Например, вы можете задать линейный или логарифмический масштаб осей (вкладка Scale (Масштаб), открытая на рис. 3.12), нормальное или инверсное направление осей ( X, У, а в случае трехмерных графиков и Z), показ сетки (параметр Grid Show), изменить стиль осей и цвета фона (вкладка Style (Стиль)), нанести у осей надписи (вкладка Label (Ярлык)) и пр. Рис. 3.13 показывает график синусоиды после некоторых операций по форматированию осей. Здесь (кстати, как и на рис. 3.12) задано построение сетки Grid по осям X и Y, построение надписей (просто буквы X и Y) по координатным осям и построение титульной надписи. Заодно на рис. 3.13 показано в открытом виде меню расширенных инструментальных средств графического окна. Его команды подробно обсуждаются в уроке 5. Словом, с объектами графики можно сделать все, что угодно! Некоторые из возможностей форматирования объектов графики мы рассмотрим позже, по мере описания типов графиков.
Рис. 3.13.Пример построения графика синусоиды после форматирования осей Если компьютер оснащен должным набором шрифтов, то надписи на графиках могут быть сделаны на русском языке — рис. 3.13 хорошо иллюстрирует эту важную для наших пользователей возможность. На нем титульная надпись сделана на русском языке. Средства форматирования надписей дают обширные возможности по выбору набора шрифтов, их стиля, размеров символов и их цвета.
Нанесение надписей и стрелок прямо на график Дополнительно на график можно нанести надписи с помощью кнопки панели инструментов с буквой А. Место надписи фиксируется щелчком мыши. На рис. 3.14 показан отформатированный график с текстовым блоком, созданным таким образом в левой верхней части поля графика. Здесь показано контекстное меню правой клавиши мыши, поясняющее выбор размера символов надписи (и другие возможности этого меню). Напоминаем, что это меню появляется при щелчке правой кнопки мыши на заданном объекте. В этом меню имеются все команды, доступные для данного объекта в данной ситуации.
Рис. 3.14.Нанесение надписи на отформатированный график Полученную таким образом надпись можно выделить и перенести мышью в любое другое место. Рис. 3.15 показывает процесс создания еще двух надписей с переносом их текстового блока в нужное место. Надписи сделаны с разным размером символов и разным стилем. Особенно приятно, что при задании на надписи возведения в степень знаком ^ надпись на экране отображается в естественном математическом виде (степень в виде верхнего индекса).
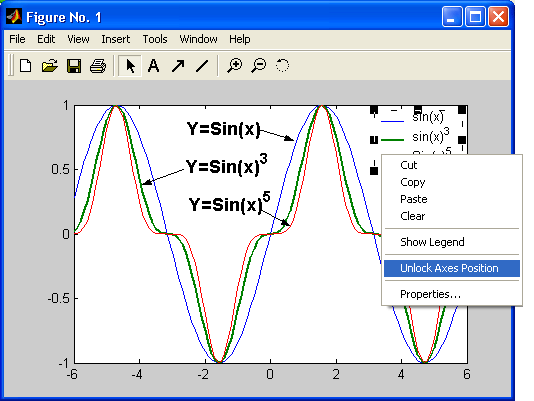
Рис. 3.15.Окончательно отформатированный график трех функций На рис. 3.15, в частности, показано задание надписей разным стилем, а также задание стрелки с помощью соответствующей кнопки панели инструментов. Это стрелку в режиме редактирования графика можно перемещать и вращать мышью, а также менять ее длину. Можно также наносить на график и обычные линии (без стрелки). Построение легенды и шкалы цветов на графике Дополнительно можно изменить размеры графика (см. меню Tools (Инструменты) и его команды Zoom In (Увеличить)и Zoom Out (Уменьшить)), начать поворот графика мышью (команда Rotate 3D), добавить отрезок прямой или иной графический примитив (подменю Add) и подключить к графику легенду — пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него. Поскольку наш график содержит три кривые, то легенда представляет собой обозначение этих трех линий в правом верхнем углу рисунка (рис. 3.16). Каждая линия имеет тот же цвет, что и на графике (и тот же стиль).
Рис. 3.16.Окончательно сформированный график Следует еще раз отметить, что все описанные возможности форматирования графиков доступны и программным способом, путем задания соответствующих графических команд, параметров и примитивов. Например команда text(х,у, 'legend') позволяет задать надпись 'legend' с началом, имеющим координаты (х, у). Если после первого апострофа перед текстом поместить параметр \leftarrow, то надпись (легенда) появится после стрелки с острием, обращенным влево. Аналогично параметр \rightarrow после надписи задает вывод стрелки после надписи с острием, обращенным вправо. Эта возможность позволяет помечать не только кривые, но и отдельные точки на них. Возможно также применение команды legend('s1', 's2',...), выводящей легенду обычного вида — отрезки линий графиков с поясняющими надписями 's1', 's2' и т.д. Перемещение графика в графическом окне Обычно график занимает фиксированное положение в центре графического окна. Однако в режиме редактирования графиков, когда курсор мыши находится в области графика, в контекстном меню правой клавиши мыши есть команда Unlock Axes Position (Отключить позиционирование осей). Она снимает фиксацию положения координатных осей графика и позволяет двигать его мышью вместе с осями. Это иллюстрирует рис. 3.17.
Рис. 3.17.Пример перемещения графика Интересно, что при перемещении графика его легенда и цветовая диаграмма остаются на прежнем месте.
Применение графической «лупы» На панели инструментов есть кнопки с изображение лупы и знаками + и -. С их помощью выполняются команды Zoom In (+)(Увеличить) и Zoom Out (-) (Уменьшить). Это позволяет увеличивать или уменьшать масштаб просмотра изображения. При этом команда Zoom In интересна еще одной возможностью — с ее помощью можно выделять часть графика перемещением мыши с нажатой левой клавишей — рис. 3.18.
Рис. 3.18.Пример выделения части графика
Рис. 3.19.Пример просмотра части графика Область выделения отмечается прямоугольником из тонких точечных линий. Отпустив левую клавишу мыши, можно наблюдать построение выделенной части графика на всем окне — рис. 3.19. С помощью команды Zoom Out можно восстановить график в прежнем масштабе. Таким образом реализуется графическая «лупа».
Урок №8. Операторы и функции · Арифметические и алгебраические операторы и функции · Операторы отношения и их функции · Логические операторы и функции · Специальные символы · Системные переменные и константы · Функции времени и даты · Элементарные функции · Тригонометрические и гиперболические функции · Функции округления и знака · Функции комплексного аргумента Начиная с этого урока мы переходим к изучению математических и логических возможностей системы MATLAB. Их изучение мы начнем с операторов и функций — тех кирпичиков, из которых строятся математические выражения. Вычисления математических выражений составляют главную цель любой системы, предназначенной для численных расчетов. Здесь мы рассмотрим полный набор операторов входного языка системы MATLAB 6.0 и соответствующих им функций. Напомним, что полный список операторов выводится командой help ops. Операторы и специальные символы системы MATLAB можно разделить на ряд категорий, которые рассматриваются ниже.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|