Модель энергетически рациональной структуры движения

Полная механическая энергия мышцы, идущая на совершение работа по перемещению звеньев нашего тела, складывается из энергии сократительного процесса (происходящего с потреблением энергии от организма) и энергии упругой деформации мышц ( практически “бесплатной” для организма). Остановимся на вопросе эффективности использования полной энергии мышцы в процессе выполнения наших движений, то есть рассмотрим модель энергетически рациональной структуры движения.

Рассмотрим этот вопрос на примере выполнения циклических движений, в которых движения биомеханических звеньев носят возвратно - вращательный характер. Возвратное движение характеризуется сменой направления движения на противоположное (туда - обратно). Например, движение маховой ноги при прыжках в длину, Обычно и прямое, и возвратное движение состоят из двух фаз: а) прямое - разгон и торможение звена; б) обратное - вновь разгон и торможение (рис.2.9). при этом наиболее характерными фазами большинства наших суставных движений являются торможение прямого движения и разгон обратного. Между этими фазами существует граничная поза, то есть положение звена, при котором происходит смена направления движения (смена направления скорости).

На рис. 2.10 представлена энергетически рациональная модель структуры возвратных движений. Рассмотрим режим работы мышц, осуществляющих движение, и их антагонистов в каждой фазе движения.

1. Прямое движение. Сгибание бедра - разгон. происходит стимуляция сократительного процесса мышц сгибателей бедра с потреблением энергии от организма. Эта энергия совершает работу по разгону звена. Как только скорость звена достигнет скорость сокращения мышцы, дальнейший разгон звена осуществляет релаксирующий последовательный упругий компонент за счет превращения накопленной потенциальной энергии упругой деформации в кинетическую энергию движения звена. Это дополнительная порция сообщаемой звену энергии, а значит, и скорости. Стимуляция сократительного процесса должна прекратиться, так как не дает механического эффекта.

Мышцы антагонисты (разгибатели бедра) не возбуждены. В конце фазы разгона начинается постепенное растягивания невозбужденного антагониста (разгибателя бедра).

2. Торможение прямого движения - сгибание бедра. Звено начинает тормозиться, когда его кинетическая энергия тратится на работе против сил тяжести звена и на работу против упругих сил растягивающегося антагониста (разгибателя бедра). Возникающие по мере растягивания антагониста все большие и большие упругие силы(нелинейная упругость, переменная жесткость) тормозят прямое движение бедра.

В граничной позе прямое движение останавливается. Скорость звена равняется нулю. Происходит смена направления движения. Вся кинетическая энергия звена израсходована на работу против сил тяжести звена и упругих сил растягивающихся, невозбужденных антагонистов.

В каком же состоянии оказываются мышцы в граничной позе к моменту начала второго возвратного движения - разгибания бедра?

Сгибатели бедра - расслаблены и возбуждены, они не удерживают сочленение в согнутом положении и не оказывают сопротивления начинающемуся возвратному движению.

Разгибатели бедра - не возбуждены, но предельно растянуты (внешней для них силой инерции звена, а не силой тяги мышц - сгибателей бедра). они накопили потенциальную энергию упругой деформации упругого компонента, на приобретение которой не потребовалось затраты химической энергии организма.

3. Обратное движение бедра. Разгон. Разгибание бедра.

Мышцы разгибателя бедра предельно растянуты, упругие силы изменяют направление движения звена на обратное. В этот момент необходимо включение в работу сократительных компонентов разгибателей бедра (должен начаться сократительный процесс как результат возбуждения мышцы). Сила тяги сократительных компонентов будет складываться с силами упругой деформации параллельного упругого компонента. Суммарная сила тяги мышцы увеличится. И опять сократительный процесс мышц бедра (с потреблением энергии от организма) должен прекратиться, как только скорость звена достигнет скорости укорочения мышцы. Дополнительную порцию кинетической энергии звено получит от последовательного упругого компонента.

4. Обратное движение. Торможение разгибателей бедра. протекает по тем же закономерностям, как и торможение прямого движения. Силы инерции звена растягивают мышцы антагонисты (сгибатели бедра). Упругие силы растягивающихся мышц сгибателей бедра тормозят движение.

К концу фазы торможения, перед моментом вторичного начала прямого движения, наблюдается следующая картина: разгибатели бедра расслаблены и не возбуждены, они не удерживают сочленение в разогнутом положении и не оказывают сопротивление начинающемуся возвратному движению (сгибанию бедра). Сгибатели бедра - не возбуждены, предельно растянуты внешней силой, накопили энергию упругой деформации для выполнения работы по разгону звена в следующей фазе движения.

Итак, сведем в единое резюме основные условия эффективного использования энергии мышечной системы в скоростно - силовых движениях:

1. В процессе движения мышца должна работать в диапазонах сильного растягивания, сокращаясь при этом на малую величину.

2, Растягивание должно быть результатом действия внешней силы (инерции), а не силы тяги антагонистов, развиваемой в текущий момент.

3. Стимуляция мышечного возбуждения (сократительный процесс мышцы) должна начинаться в фазе наибольшего удлинения мышцы.

4. При стимуляции возбуждения должно особо акцентироваться начало процесса (обеспечиваться возможно большая мощность первого рывка).

5. Активное сокращение мышцы (возбудительный процесс) должно делаться лишь до тех пор, пока это дает механический эффект.
3. УПРАЖНЕНИЯ С СОХРАНЕНИЕМ ПОЛОЖЕНИЯ ТЕЛА
3.1. Общая характеристика статических положений
При выполнении многих физических упражнений и спортивных движений человеку необходимо сохранять неподвижное положение тела или, как принято называть, статическое положение. Например, как исходное - различные стартовые положения, как промежуточные - всевозможные висы, упоры, стойки, как конечное - фиксация штанги на вытянутых руках.
В каждой из спортивных специализаций есть множество примеров статичных упражнений, которые являются важным элементом спортивной техники. В зависимости от принадлежности к той или иной фазе движения статические положения несут определенную функциональную нагрузку в целостном движении и играют свою особую роль в решении основной двигательной задачи.
Изучение биомеханики физических упражнений мы начинаем с биомеханического анализа статических положений как важного и своеобразного элемента спортивной техники, определяющего в ряде спортивных движений эффективность решения основной двигательной задачи.
Биомеханическая функциональная роль статических положений в целостном спортивной движении будет различной в зависимости от данного статического положения. Так, например, одной из задач правильного исходного статического положения штангиста перед подъемом штанги является задача - не допустить перегрузки межпозвоночных дисков в по-следующий момент подъема штанги (рис.3.1). Статическое положение с сохранением нормального поясничного лордоза устраняет сдавливание межпозвоночных дисков. В момент же фиксации штанги на вытянутых руках - основная задача принять такое статическое положение, которое бы обеспечило необходимую степень устойчивости равновесия механической системы “человек - штанга”.
Можно сравнить по биомеханическому функциональному значению и роли в решении двигательной задачи следующие статистические положения: стартовые положения в локомоторных движениях, стойки врата-рей, стойки волейболистов перед приемом мяча, защитные стойки в баскетболе, удержание упора, виса или стойки в гимнастике или акробатике и т.д. Необходимо помнить, что любая смена направления движения спорт-смена происходит через мгновенную статическую позу.
Огромная роль статических положений в спортивных движениях предполагает их специальное биохимическое изучение и анализ.

Рис. 3.1 Нагрузка на межпозвоночные диски при подъеме штанги:
а - правильное исходное положение, б - неправильное.

Рис.3.2 Проекция вектора силы на координатные оси.
Следует помнить, что термин “статическое положение” не совсем точен. Чистая статика наступает лишь после смерти. В живой системе происходят живые процессы дыхания, кровообращения, мышечного тремора, что приводит к смещению масс тела, а следовательно, и нарушению условий статики. Поэтому биомеханический анализ упражнений с сохранением положения тела как статических положений мы будем производить в рамках определенных допущений, которые оговорим несколько позже.
Сохранение положения тела (статическое положение) характеризуется: 1) позой, то есть взаимным относительным положением звеньев тела, необходимым для выполнения определенной двигательной задачи; 2) ориентацией и местоположением в пространстве; 3) отношением к опоре.
В статическом положении тело человека как биомеханическая система (элементы этой системы - отдельные звенья тела человека) находится в равновесии.
Равновесие механической системы под действием приложенных к ней сил - это такое состояние, при котором координаты всех точек системы постоянны (неизменяемы во времени) по отношению к неподвижной системе отсчета.
О равновесии мы можем говорить и в случае сохранения позы в движении, то есть в случае так называемой динамической позы, при которой скорость изменения координат хотя бы одного из звеньев не равна нулю. В случае динамической позы силы, действующие на отдельные звенья тела, не должны изменять их взаимного относительного положения, то есть не должны вызывать движения этих звеньев друг относительно друга.
Итак, для сохранения и положения позы тела нам необходимо со-стояние, при котором выполняется условие равновесия сил, действующих на биомеханическую систему.
Изучение условий равновесия механической системы под действием приложенных к ней сил является одной из основных задач раздела общей механики, который называется “Статика твердого тела”. В разделе “Статика” излагаются два основных вопроса: 1) учение о силах и условиях равновесия материальных тел под действием системы сил; 2) учение об обыщем центре тяжести тела (ОЦТ).

3.2. Определение координат ОЦТ тела спортсмена
На каждую частицу тела, находящегося в поле земного тяготения действует направленная к центру Земли сила, называемая силой тяжести. По величине сила тяжести равна массе тела, помноженной на ускорение свободного падения: P = m*g.
Ввиду малого размера тел, с которыми обычно приходится иметь дело, относительно размеров Земли, мы считаем силы тяжести частиц тела направленными вертикально вниз и параллельными друг другу. Если элементарные силы тяжести, действующие на отдельные частицы тела, есть P1, P2, P3,... Pn , а равнодействующая этих параллельных сил - Р, то модуль этой силы:

Точка, через которую проходит действие равнодействующей элементарных сил тяжести при любом повороте тела в пространстве, являющаяся центром параллельных сил тяжести, называется общим центром тяжести (ОЦТ) твердого тела. Так как тело человека не является твердым неизменяемым телом, а представляет из себя систему взаимно подвижных звеньев, то положение ОЦТ будет определяться главным образом, позой тела человека (то есть взаимным относительным расположением звеньев тела) и изменяться с изменением позы.
Знание положения ОЦТ тела человека важно для биомеханического анализа и для решения многих самостоятельных задач механики спортивных движений. Часто по движению ОЦТ мы судим о движении тела чело-века в целом, оцениваем как бы результат движения. Положение ОЦТ метаемых снарядов определяет их аэродинамические свойства. По характеристикам движения ОЦТ (траектории, скорости, ускорения) можно судить о технике выполнения движения. В безопорном положении движения всех звеньев тела человека происходит вокруг осей, проходящих через ОЦТ. На характеристики движения самого ОЦТ во время безопорного положения мы повлиять не можем, так как программа движения ОЦТ в полетной фазе задается в процессе взаимодействия спортсмена с опорой.
По положению ОЦТ тела спортсмена мы оцениваем статические положения (стартовые, промежуточные, конечные), так как положение ОЦТ характеризует степень устойчивости равновесия. Степень напряжения тех или иных мышечных групп в статическом положении зависит от положения ЦТ звена и вышележащих звеньев. Положение ОЦТ зависит от распределения масс тела (от конструкционных особенностей) и этим определяет двигательные возможности человека.
Говоря об ОЦТ тела человека, следует иметь в виду не геометрическую точку, а некоторую область пространства, в которой эта точка перемещается. Это перемещение обусловлено процессами дыхания, кровообращения, пищеварения, мышечного тонуса и др., то есть процессами, при-водящими к постоянному смещению масс тела человека. Ориентировочно можно считать, что диаметр сферы, внутри которой происходит перемещение ОЦТ, в спокойном состоянии составляет 10 - 20 мм. В процессе же движения смещение ОЦТ может значительно увеличиваться и при этом оказывать влияние на технику выполнения движений.
Координаты ОЦТ тела человека по фотографии определяются аналитическим путем на основании формулы:

3.3. Основные понятия статики
Перед тем как приступить к выяснению условий равновесия материальных тел под действием системы сил, введем некоторые теоретические понятия.
В статике будем рассматривать только силовые отношения, не выясняя природу (причину) возникновения этих сил. Под силой мы понимаем количественную меру механического взаимодействия тел.
Силы, действующие на человека в основной стойке: 1) сила тяжести его тела или других тел (снарядов, партнеров), 2) сила реакции опоры (вес приложен к опоре, реакция опоры - к человеку). Это внешние по отношению к телу человека силы (результат взаимодействия тела человека с другими телами - землей и опорой).
Тело человека - не твердое тело, а система подвижно соединенных звеньев. Для сохранения позы (то есть взаимного относительного расположения подвижных звеньев тела) необходимо закрепить суставы (более 240 степеней свободы, то есть 240 возможных передвижений). Это закрепление, фиксация суставов, обеспечивается силами мышечных тяг. Мышечные силы - это внутренние силы для тела человека. Мышцы своим напряжением обеспечивают сохранение позы и положения, они заставляют как бы “отвердеть” систему взаимно подвижных звеньев человеческого тела. Следует подчеркнуть, что для сохранения позы особую роль играют мышцы. Часто условия действия внешних сил таковы, что равновесие воз-можно ( “крест” на кольцах, “флажок“ на шведской стенке) , но человек не может сохранить свое положение и позу потому, что недостаточно сильны его мышцы. У разных людей свои предельные позы.

Рис.3.3 Момент силы тяжести гимнаста (МО) относительно оси перекладины.

Чтобы задать силу, надо знать: 1) ее величину (модуль), 2) направление, 3) точку приложения. Силы, как вектора, можно вычитать, складывать, умножать.
Решение многих задач по определению условий равновесия тела под действием системы сил связано с операцией геометрического сложения (вычитания) сил.
Одним из условий равновесия является необходимость того, чтобы геометрическая сумма всех сил, то есть главный вектор был равен нулю :
Силовой многоугольник должен быть замкнут (конец последней силы сов-падает с началом первой). Если главный вектор не равен нулю, то система сил приводится к одной силе, а под действием одной силы тело не может находиться в равновесии. Проекция силы на ось. Часто при решении задач статики оперируют не векторами сил, а их проекциями на координатные оси (рис.3.2). Проекцией силы на ось называется скалярная величина, равная длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак “плюс”, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак “минус” - если в отрицательном. Если сила перпендикулярна оси, то ее проекция равна нулю.
Моментом силы относительно точки на плоскости называется век-торная величина, по модулю равная произведению силы на плечо силы (плечом силы является кратчайшее расстояние между точкой, относительно которой изменяется момент силы, и направлением действия силы). Пример: гимнаст на перекладине (рис 3.3). Момент силы тяжести гимнаста : Мо = G * r. Если видим вращение почасовой стрелке, то такой момент отрицательный, и наоборот.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил (рис.3.4).
Система сил, образующих пару, не находится в равнодействии и не имеет равнодействующей. Действие пары сил на тело сводится к некоторому вращательному эффекту. Момент пары сил - это произведение модулю одной из сил на плечо: М = ±F * r.
Аксиома освобождаемости от связей. Равновесие твердого тела не изменится, если мы мысленно освободимся от связей, наложенных на данное тело, и заменим действие этих связей их реакциями.
Свободным телом называют тело, не связанное с другими телами. Оно может перемещаться в любых направлениях под действием приложенных к нему сил. Например, летящий мяч, ядро, тело спортсмена в без-опорной фазе. Обычно тела как то соединены, связаны друг

а б

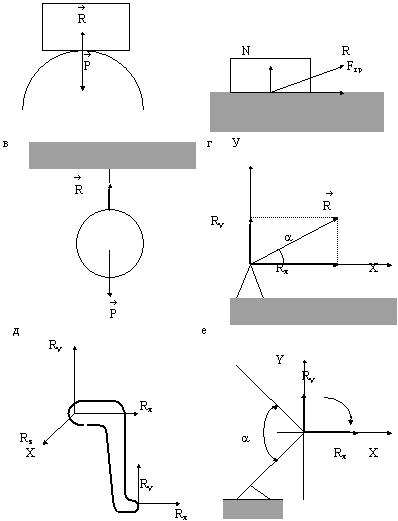
Рис.3.5 Направление реакции связи при разных видах связей.

с другом, в результате чего перемещения этих тел ограничены. Одно тело ограничивает, мешает перемещению другого. Если тело ограничено в своих перемещениях, то говорят, что тело не свободно, на это тело наложены связи. Связью в механике называется всякое другое тело, которое ограничивает перемещение тела (объекта) в определенном направлении.
Пример связей: пол, гриф перекладины, торы колец и т.д. Для от-дельных звеньев человеческого тела, соединенных друг с другом связями, ограничивающими их перемещения, являются такие анатомические образования, как суставные поверхности, суставные сумки, связки мышцы. Сила с которой связь действует на тело, препятствуя его перемещению, называется силой реакции связи. По величине сила реакции связи равна силе давления нашего тела на связь и направлена в сторону, противоположную этому давлению.
Реакция связи существует только тогда, когда данное тело воздействует на связь. Реакция связей - это реактивные (ответные) силы.
При анализе физических упражнений необходимо уметь определять реакции связей (по величине и направлению), так как реакция связей определяет характер воздействия связи на наше тело. В большинстве случаев направление его является сложной задачей.
Познакомимся с основными видами связей: 1) реакции идеально гладкой поверхности. Трением о такую поверхность можно пренебречь. Такая поверхность не дает телу перемещаться только вертикально вниз (по нормали к поверхности). Поэтому реакция связи идеально гладкой поверхности направлена перпендикулярно (по нормали) к поверхности со-прикасающихся тел в точке их касания (рис.3.5а); 2) реакция шероховатой поверхности. Такая поверхность не дает телу перемещаться вниз по нормали и вдоль поверхности. Направление реакции связи здесь заранее не известно. Поэтому в этом случае раскладывают полную реакцию связи на две составляющие по тем направлениям, по которым связь не дает перемещаться телу (рис 3.5б): одна составляющая N - по нормали к поверхности, вторая составляющая Fтр - вдоль поверхности. По величине полная реакция связи равна:

Направление реакции связи определяется соотношением:

3) реакция стержня. Стержень не дает телу удаляться от точки подвеса. Поэтому реакция стержня или натянутой нити натянута вдоль стержня или натянутой нити в точке ее подвеса (рис.3.5в); 4) неподвижная шарнирная опора. Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа (рис.3.5г). Необходимо разложить полную реакцию связи на ее составляющие Rx и Ry по направлению осей координат. По величине полная реакция связи равна:

Направление ее определяется соотношением:

Связи, наложенные на сустав, реализуются через анатомическое строение сустава (форма суставных поверхностей, суставные сумки, связки, мышцы, окружающие сустав).
Реакция связи в плечелоктевом сочленении (блоковидный шарнир) имеет неопределенное направление в плоскости плечевой и локтевой кости (рис.3.5д).
Реакция связи, возникающая в плечевом суставе (шаровой шарнир) имеет неопределенное пространственное направление (рис.3.5д). Для определения направления реакции связи плоской фигуры реакцию связи за-меняют двумя ее составляющими, Наиболее удобно за их направление взять вертикальную и горизонтальную составляющие. Реакция связи - это сила, которая препятствует поступательному перемещению одного звена относительно другого.
Но в суставе возможно еще и вращение звена относительно другого. В статической позе имеет место фиксация суставного угла между звенья-ми, то есть наложена связь на вращательное движение, а следовательно, имеет место момент реакции связи. Реализуется момент реакции связи через суставные мышечные моменты. Пример: соединение бедра и голени.
Бедро является связью для голени. Реализуется эта связь через анатомические образования коленного сустава и мышцы, окружающие ко-ленный сустав. Какие на голень наложены связи? Коленный сустав не позволяет голени "оторваться" от бедра, то есть препятствует поступательному перемещению голени вдоль координатных осей Х и У (вправо - влево; вверх - вниз). Это первый вид связи. Кроме того, фиксированный в данной позе суставной угол a между бедром и голенью (фиксация этого угла осуществляется мышечными моментами) не позволяет голени вращаться относительно бедра. Это второй вид связи.
Если мысленно отбросить связь (бедро), производя расчленение в коленном суставе, то действие связи на голень необходимо заменить (рис.3.5е):
1) в соответствии с первым видом связи - силой реакции связи (так как она имеет неопределенное направление в плоскости чертежа, то заменяем ее двумя составляющими, направленными вдоль координатных осей Rx и Ry);
2) в соответствии со вторым видом связи - момент реакции связи Мм.
Направление составляющих реакции связи, а также момента реакции связи выбирается произвольно. Если в процессе решения задачи составляющие реакции или момент получатся отрицательными, значит действительное их направление будет противоположно тому, которое выбрано на чертеже.
Определение сил реакции связи в суставе при удержании тех или иных статических положений позволяет оценить нагрузку на сустав (что-бы избежать травм). А определение моментов реакции связи позволяет рассчитать величину и направление управляющих мышечных моментов, которые необходимо приложить, чтобы зафиксировать данную статическую позу, то есть иными словами, оценить степень участия тех или иных мышечных групп в удержании данного статического положения.
3.4. Определение условий равновесия звеньев тела в статическом положении.
Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись два условия:
1) главный вектор всех сил должен равняться нулю:

2) главный момент всех действующих сил относительно любой точки плоскости тоже должен равняться нулю:

Главный вектор R может равняться нулю только тогда, когда одно-временно

Следовательно, условия равновесия будут выполняться в том случае, если одновременно будет:

Для равновесия произвольной плоскости системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.
Для рассмотрения условий равновесия тела человека в статическом положении примем ряд допущений:
1. Тело человека будем рассматривать как механическую систему, состоящую из определенного числа звеньев.
2. Звенья тела будем моделировать в виде недеформируемых стержней.
3. Суставы, соединяющие звенья тела, будем моделировать в виде идеальных шарниров (трение в шарнире отсутствует).
4. Количество звеньев в выбранной расчетной схеме будет определяться желаемой точностью описания статического положения с помощью механической модели.
5. Необходимая жесткость механической модели (сохранение стати-ческой позы - взаимного относительного положения звеньев тела) обеспечивается суставными моментами, которые реализуется моментами сил мышечных тяг, обслуживающих данный сустав.
В статическом положении тело человека, как биомеханическая система (элементы этой системы - отдельные звенья тела), находится в равновесии.
Равновесие механической системы под действием приложенных к ней сил - это такое состояние, при котором координаты всех точек системы постоянны ( неизменяемы во времени) по отношению к неподвижной системе отсчета.
Если тело находится в равновесии при действии на него системы сил, то должны удовлетворяться следующие условия:
1. Сумма проекций всех сил на координатную ось Х равняется нулю: n

1. Сумма проекций всех сил на координатную ось У равняется нулю: n

3. Главный момент, равный сумме моментов всех действующих сил относительно оси вращения (имеется в виду ось вращения в конкретном суставе), равен нулю:

По механическому смыслу первые два условия выражают необходимость того, чтобы тело не имело перемещений вдоль координатных осей, а третье является условием отсутствия вращения в плоскости ОХУ.
Решение уравнений равновесия позволяет:
1. Найти численное значение всех сил или моментов сил, действующих на механическую систему (опорно - двигательный аппарат спортсмена) , находящуюся в состоянии равновесия.
2. Определить характер действия всех этих сил или моментов на ОДА спортсмена (растяжение, сжатие, сдвиг, кручение и т.д.).
Одни силы, действующие на ОДА спортсмена, находящегося в со-стоянии равновесия, являются известными (заданными), например, силы тяжести отдельных звеньев тела, силы тяжести снаряда, партнера и т.д., характер их действия известен. Другие силы неизвестны. Такими неизвестными силами обычно являются силы мышечных тяг (или управляющие мышечные моменты), удерживающие сочленения в данной позе, а также реакции связей, наложенных на ОДА (это могут быть реакции связей суставов или опоры). Решение уравнений равновесия позволяет найти неизвестные силы или моменты, а также определить характер их действия на ОДА спортсмена.
Для плоской механической системы мы имеем три уравнения равновесия. Следовательно, решив эти уравнения, мы можем найти три неизвестные силы. Если неизвестных сил больше трех, то задача становится статически неопределимой.
Уравнения равновесия выведены и справедливы для свободных тел, то есть тел, на которые не наложены механические связи. В реальной жизни нам, как правило, приходится сталкиваться и рассматривать условия равновесия не свободных, а связанных тел, на движение которых наложены определенные механические ограничения - связи.
Поэтому для того, чтобы иметь право применять к этим реальным несвободным телам уравнения равновесия, необходимо представить их как свободные тела, то есть используя аксиому освобождаемости от связей, мысленно отбросить связи и заменить действие связей силами реакции связей.
Порядок решения задачи:
1. Выделить объект равновесия.
2. Изобразить на чертеже все заданные активные силы.
3. Мысленно отбросить связи, наложенные на тело, и заменить действие связей их реакциями (изобразить реакции связей на чертеже).
4. Рассмотреть равновесие несвободного тела как свободного, находящегося под действием активных сил и реакций связей.
5. Записать условия равновесия согласно условиям равновесия.
6. Решить уравнения равновесия и найти искомые величины.

ПРИМЕР. В положении "присед" определить момент мышечных сил и реакции связей в коленном суставе правой ноги (рис.3.6).

РЕШЕНИЕ ЗАДАЧИ:
1. Тело человека моделируем как механическую систему, удовлетворяющую принятым допущениям.
2. Выбираем объект равновесия - правые голень и стопа.
3. Избираем активные силы:
Рг - сила тяжести голени;
Рст - сила тяжести стопы.
Точки приложения сил - это центры тяжести соответствующих звеньев.
4. Мысленно отбросим связи, наложенные на объект равновесия, и заменим их действие реакциями связей. Со стороны опоры реакция связи будет приложена к стопе и числено равна весу тела R = P.
Бедро является связью для голени. Реализуется эта связь через анатомические образования коленного сустава мышцы, обслуживающей ко-ленный сустав.
Какие связи наложены на голень? Коленный сустав не позволяет голени "оторваться" от бедра, то есть препятствует поступательному перемещению голени вдоль координатных осей Х и У (вправо - влево, вверх - вниз). Это первый вид связи. Кроме того фиксированный в данной позе суставной угол a между бедром и голенью (фиксация этого угла осуществляется мышечными моментами) не позволяет голени вращаться вокруг бедра. Это второй вид связи.
Если мысленно отбросить связь (бедро), производя расчленение в коленном суставе, то действие связи на голень необходимо заменить:
а) в соответствии с первым видом связи - силой реакции связи (так как она имеет неопределенное направление в плоскости чертежа, то заменяем ее двумя составляющими, направленными вдоль координатных осей Х и У) Rkx и Rky;
б) В соответствии со вторым видом связи - момент реакции связи Мk.
Направление составляющих реакции связи, а также момента реакции связи выбирается произвольно.
5. Рассмотрим равновесие свободного тела - голени и стопы в плоскости xky. Это тело находится под действием активных сил Рг и Рст, реакций R, Rkx и Rky и момента Мk. Составим уравнения равновесия: n
(1)
(2)
(3)
Силы Rkx и Rky относительно оси вращения в коленном суставе момента не составляют, так как они пересекают эту ось.
Решая уравнения (1), (2), (3), получим:

величина силы R числено равна весу тела.

Не нашли, что искали? Воспользуйтесь поиском по сайту: