
|
|
Сети идеальных элементов; правила КирхгофаS 4. Эквивалентные контуры Энергия Лестничная сеть Фильтры Другие элементы цепи Повторить: гл.2 (вып. 2) «Алгебра»; гл. 23 (вып. 2) «Резонанс»; Гл. 25 (вып. 2) «Линейные системы и обзор» Импедансы В основном наши усилия при чтении этих лекций были направлены на то, чтобы получить полные уравнения Максвелла. В предыдущих двух главах мы обсудили следствия этих уравнений. Выяснилось, что они содержат объяснение всех статических явлений, которые мы изучали раньше, и явлений электромагнитных волн и света — вопроса, подробно изучавшегося в самом начале нашего курса. Уравнения Максвелла дают и то и другое, смотря по тому, где эти поля вычисляются: поблизости от токов и зарядов или же вдали от них. Есть и промежуточная область, но о ней ничего интересного сказать нельзя; там никаких особых явлений не происходит. Но в электромагнетизме остается еще несколько вопросов, которые стоит осветить. Надо будет обсудить вопрос связи относительности и уравнений Максвелла, т. е. выяснить, что произойдет, если на уравнения Максвелла посмотреть из движущейся системы координат. Важен еще и вопрос о сохранении энергии в электромагнитных системах. Кроме того, существует обширная область электромагнитных свойств материалов; до сих пор мы рассматривали только электромагнитные поля в пустом пространстве, если не считать изучения свойств диэлектриков. Да и при изучении света все еще оставалось несколько вопросов, которые хотелось бы рассмотреть еще раз с точки зрения уравнений поля. В частности, надо бы еще раз вернуться к вопросу о показателе преломления (особенно у плотных веществ). Наконец, интересны явления, связанные с волнами, заключенными внутри ограниченной области пространства. Мы кратко коснулись этой проблемы, когда изучали звуковые волны. Но уравнения Максвелла тоже приводят к решениям, которые представляют волны электрических и магнитных полей, замкнутые в некотором объеме. В одной из последующих глав мы рассмотрим этот вопрос, имеющий важные технические применения. И чтобы подойти к нему, мы начнем с того, что изложим свойства электрических цепей при низких частотах. После этого мы сможем сравнить такие системы, когда к уравнениям Максвелла применимо почти статическое приближение, и системы, в которых преобладают высокочастотные эффекты. Итак, снизойдем с величественных и труднодоступных высот последних нескольких глав и обратим свой взор на сравнительно низменную задачу — задачу об электрических цепях. Впрочем, мы убедимся в том, что даже столь мирские дела оказываются весьма запутанными, если в них вникнуть достаточно глубоко. В гл. 23 и 25 (вып. 2) мы уже обсуждали некоторые свойства электрических цепей (контуров). Теперь мы повторим часть изложенного там материала, но более подробно. Мы по-прежнему будем иметь дело с линейными системами и с напряжениями и токами, которые меняются синусоидально; поэтому мы можем представить все напряжения и токи в виде комплексных чисел, пользуясь экспоненциальными обозначениями, введенными в гл. 22 (вып. 2). Так, меняющееся во времени напряжение V(t) будет записываться в виде
(22.1)
где
(22.2) и т. д. Большей частью мы будем писать уравнения, пользуясь обозначениями V, I, e, ... (вместо В прежних наших рассуждениях об электрических цепях мы полагали, что такие вещи, как индуктивность, емкость и сопротивление, вам знакомы. Сейчас мы немного подробнее объясним, что понимают под этими идеализированными элементами схем. Начнем с индуктивности.
Фиг. 22.1. Индуктивность. Индуктивность — это навитая в несколько рядов проволока в форме катушки, два конца которой выведены к зажимам на некотором расстоянии от катушки (фиг. 22.1). Предположим, что магнитное поле, создаваемое токами в катушке, не очень распространяется на все пространство и не воздействует на другие части цепи. Обычно этого добиваются, придав катушке форму лепешки или намотав ее на подходящий железный сердечник (это сжимает магнитное поле); можно еще поместить катушку внутрь металлической коробочки: схематически это показано на фиг. 22.1. В любом случае предполагается, что во внешней области у зажимов а и b магнитным полем можно пренебречь. Кроме того, мы будем считать, что электрическое сопротивление проводов в катушке можно не учитывать. И наконец, полагают, что можно пренебречь и электрическим зарядом, возникающим на поверхности провода, когда создаются электрические поля.
(22.3)
где L — индуктивность катушки. Поскольку dI/dt=iwI, то мы имеем
(22.4) Тот способ, которым мы описали идеальную индуктивность, иллюстрирует общий подход к другим идеальным элементам цепи — обычно их называют «сосредоточенными» элементами. Свойства элемента полностью описываются на языке токов и напряжений, возникающих на его зажимах. Прибегнув к подходящим приближениям, можно игнорировать огромную сложность тех полей, которые возникают внутри объекта. То, что происходит внутри, отделяется от того, что происходит снаружи. Для всех элементов цепи мы намерены сейчас найти соотношения, подобные формуле (22.4). В ней напряжение пропорционально силе тока с константой пропорциональности, которая, вообще говоря, есть комплексное число. Этот комплексный коэффициент пропорциональности называется импедансом, и его привыкли обозначать через z (не следует путать с координатой z). В общем случае это функция частоты w. Стало быть, для каждого сосредоточенного элемента мы напишем
(22.5)
Фиг. 22.2. Емкость (или конденсатор). Рассмотрим с этой точки зрения емкость . Она состоит из двух проводящих пластин (обкладок), от которых к нужным зажимам отходят два провода. Пластины могут быть любой формы и часто отделяются друг от друга каким-нибудь диэлектриком. Это схематически изображено на фиг. 22.2. Мы снова делаем несколько упрощающих предположений. Мы считаем, что пластины и провода — идеальные проводники, а изоляция между пластинами тоже идеальна, так что через нее никакие заряды с пластины на пластину перейти не могут. Затем мы предполагаем, что проводники находятся близко друг от друга, но зато аначительно удалены ото всех остальных проводников, так что все линии поля, выйдя из одной пластины, непременно оканчиваются на другой. И тогда заряды на пластинах всегда равны и противоположны друг другу, причем по величине намного превосходят величину заряда на поверхности проводов. И наконец, мы считаем, что поблизости от конденсатора магнитных полей нет. Рассмотрим теперь контурный интеграл от Е вдоль замкнутой петли, которая начинается на клемме а, проходит внутри провода до верхней обкладки конденсатора, перескакивает промежуток между пластинами, проходит с нижней обкладки на клемму b и возвращается к клемме а по пространству снаружи конденсатора. Раз магнитного поля нет, контурный интеграл от Е по этому замкнутому пути равен нулю. Интеграл можно разбить на три части:
Интеграл вдоль проводов равен нулю, потому что внутри идеальных проводников электрического поля не бывает. Интеграл от зажима b до а снаружи конденсатора равен разности потенциалов между клеммами со знаком минус. А поскольку мы считаем, что обкладки как-то изолированы от прочего мира, то общий заряд двух обкладок должен быть равен нулю; и если на верхней обкладке есть заряд Q, то на нижней имеется заряд —Q. Раньше мы уже видели, что если заряды двух проводников равны и противоположны, +Q и -Q, то разность потенциалов между ними есть Q/C, где С — емкость этих проводников. Из (22.7) следует, что разность потенциалов между зажимами а и b равна разности потенциалов между обкладками. Поэтому
или
(22.8) Тогда импеданс z конденсатора равен
(22.9)
Фиг. 22.3. Сопротивление. Отсюда следует, что ток I через сопротивление пропорционален напряжению V на зажимах:
где R называется сопротивлением. Позже мы убедимся, что связь между силой тока / и напряжением V для реальных проводящих материалов только приближенно можно считать линейной. Мы убедимся также, что считать эту приближенную пропорциональность не зависящей от частоты изменений тока и напряжения можно лишь тогда, когда частота не слишком высока. И тогда для переменных токов напряжение на зажимах оказывается в фазе с током, а это значит, что сопротивление — число действительное:
(22.10) Результаты наших рассуждений о трех сосредоточенных элементах цепи — индуктивности, емкости, сопротивлении — подытожены фиг. 22.4. На этом рисунке, как и на предыдущих, напряжение отмечено стрелкой, направленной от одной клеммы к другой. Если напряжение «положительно», т. е. если на клемме а потенциал выше, чем на клемме b, то стрелка указывает направление «падения напряжения».
Фиг. 22.4. Идеальные сосредоточенные элементы цепи (пассивные). При нулевой частоте, т. е. при постоянном токе, импеданс индуктивности стремится к нулю; между клеммами наступает короткое замыкание. Импеданс же емкости при постоянном токе стремится к бесконечности; цепь между клеммами размыкается. Принимать в расчет при постоянных токах нужно только обычные сопротивления: они не зависят от частоты. В описанных до сих пор элементах цепи ток и напряжение были пропорциональны друг другу. Если одно равно нулю, то и другое равно нулю. Обычно мы мыслим на таком языке: приложенное напряжение «ответственно» за ток или ток «создает» напряжение на клеммах. Элемент словно в некотором смысле «отвечает» на «приложенные» внешние условия. По этой причине такие элементы называются пассивными. Тем самым их можно противопоставить активным элементам, таким, как генераторы, которые мы рассмотрим в следующем параграфе и которые представляют собой источники колебаний токов или напряжений в цепи. Генераторы Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе. Пусть у нас имеется катушка, наподобие катушки самоиндукции, но только витков у нее немного и на магнитное поле ее собственного тока можно внимания не обращать. Эта катушка, однако, находится в переменном магнитном поле, подобном тому, какое создается вращающимся магнитом (фиг. 22.5). (Мы уже видели ранее, что такое вращающееся магнитное поле можно также создать с помощью подходящей совокупности катушек с переменными токами.) Сделаем снова несколько упрощающих допущений. Это все те же допущения, которые мы делали, говоря об индуктивности. В частности, мы предполагаем, что меняющееся магнитное поле ограничено лишь небольшой областью поблизости от катушки и за пределами генератора, в пространстве
Фиг. 22.6. Обозначение идеального генератора. Повторяя опять в точности тот же анализ, что и для индуктивности, рассмотрим контурный интеграл от Е вдоль замкнутой петли, которая начинается на зажиме а, проходит по катушке до зажима bи возвращается к началу по пространству между зажимами. Снова заключаем, что разность потенциалов между зажимами а и bравна всему интегралу от Е вдоль петли:
(22.11) Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. e(t). Такой идеальный генератор представляют символом, показанным на фиг. 22.6. Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V=e с более высоким потенциалом на зажиме а. Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7). Мы изобразили магнитную палочку, чтобы показать наличие магнитного поля, но его можно, конечно, заменить любым другим источником постоянного магнитного поля, скажем добавочной катушкой, по которой течет постоянный ток. Как показано на рисунке, вращающаяся катушка связана с внешним миром скользящими контактами, или «кольцами». Нас опять интересует разность потенциалов, которая появляется между клеммами а и b, т. е. интеграл от электрического поля между а и b по пути снаружи генератора. Теперь в этой системе уже нет изменяющихся магнитных полей и на первый взгляд кажется удивительным, откуда на зажимах генератора берется напряжение. Действительно, ведь нигде же внутри генератора нет никаких электрических полей. Мы, как обычно, предполагаем для наших идеальных элементов, что внутри них провода сделаны из идеально проводящего материала; а, как уже неоднократно повторялось, электрическое поле внутри идеального проводника равно нулю. Но это не всегда верно. Это неверно тогда, когда проводник движется в магнитном поле. Правильное утверждение таково: общая сила, действующая на произвольный заряд внутри идеального проводника, должна быть равна нулю. Иначе в нем возник бы бесконечный ток свободных зарядов. Так что надо брать сумму электрического поля Е и векторного произведения скорости проводника v на магнитное поле В; это есть полная сила, действующая на единичный заряд, и вот она-то всегда равна нулю: F=E+vXB=0 (в идеальном проводнике). (22.12) А наше прежнее утверждение о том, что внутри идеальных проводников электрических полей не бывает, верно лишь тогда, когда скорость проводника v равна нулю; в противном случае справедливо выражение (22.12). Вернемся к нашему генератору, показанному на фиг. 22.7. Теперь мы видим, что контурный интеграл от электрического поля Е между зажимами а и bпо проводящим путям генератора должен быть равен контурному интегралу от vXB по тому же пути;
Однако по-прежнему остается верным, что контурный интеграл от Е по замкнутой петле, включая возвращение от зажима b к а вне генератора, должен быть равен нулю, потому что меняющиеся магнитные поля отсутствуют. Так что первый интеграл в (22.13) по-прежнему равен V — напряжению на зажимах. Оказывается, что интеграл в правой части (22.13) просто равен быстроте изменения потока через катушку, а значит, по правилу потока, равен э.д.с. катушки. И опять получается, что разность потенциалов между зажимами равна э.д.с. цепи в согласии с уравнением (22.11). Так что все равно, какой у нас генератор: меняется ли в нем магнитное поле возле закрепленной катушки, вертится ли в закрепленном магнитном поле катушка,— внешние свойства генераторов одни и те же. На клеммах всегда существует напряжение V, которое не зависит от тока в цепи, а определяется только условиями внутри генератора, формируемыми по нашему произволу. Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8. Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее.
Фиг. 22.8. Химический элемент. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента. Рассуждая так же, как это мы делали, когда говорили об идеальном конденсаторе, мы убедимся, что, если нет избытка диффузии ионов какого-либо знака, разность потенциалов между зажимами а и b равна просто контурному интегралу от электрического поля между электродами. Конечно, между конденсатором и таким химическим элементом есть существенная разница. Если на мгновение закоротить выводы конденсатора, он разрядится и разности потенциалов между выводами уже не будет. В случае же химического элемента ток с зажимов можно снимать непрерывно, никак не изменяя при этом э.д.с., пока, конечно, реактивы в элементе не израсходуются. Известно, что в реальном элементе разность потенциалов на зажимах убывает по мере возрастания снимаемого с него тока. Но при нашей идеализации задачи легко себе представить, что у нас есть идеальный элемент, в котором напряжение на электродах не зависит от силы тока. Тогда реальный элемент можно рассматривать как идеальный, соединенный последовательно с сопротивлением. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

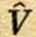 — комплексное число, не зависящее от t. При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V(t) представляется действительной частью комплексной функции в правой части уравнения.
— комплексное число, не зависящее от t. При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V(t) представляется действительной частью комплексной функции в правой части уравнения.
 ...), помня при этом, что они изменяются со временем всегда так, как в (22.2).
...), помня при этом, что они изменяются со временем всегда так, как в (22.2).






















