
|
|
Предел последовательности и функции. Теоремы о пределахМАТЕМАТИЧЕСКИЙ АНАЛИЗ Предел функции Предел последовательности и функции. Теоремы о пределах Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству êxn - a ê < e. (1.1) Записывают это следующим образом: Неравенство (1.1) равносильно двойному неравенству a- e < xn < a + e, (1.2) которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а. Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся. Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n. Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему. Определение 1. Постоянное число А называется пределом функции f(x) при x®a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А. Это определение называют определением предела функции по Гейне, или “на языке последовательностей”. Определение 2. Постоянное число А называется пределом функции f(x) при x®a, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d-окрестности числа а, т.е. для x, удовлетворяющих неравенству Это определение называют определением предела функции по Коши, или “на языке e - d“. Определения 1 и 2 равносильны. Если функция f(x) при x ® a имеет предел, равный А, это записывается в виде
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной. Для нахождения пределов на практике пользуются следующими теоремами. Теорема 1. Если существуют пределы
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”. Теорема 2. т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,
Теорема 3.
где e » 2.7 - основание натурального логарифма. Формулы (1.10) и (1.11) носят название первого и второго замечательного пределов. Используются на практике и следствия формулы (1.11):
в частности,
Eсли x® a и при этом x > a, то пишут x® a+0. Если, в частности, a=0, то вместо символа 0+0 пишут +0. Аналогично если x®a и при этом x<a, то пишут x®a-0. Числа Функция f(x) называется непрерывной в точке x0, если
Условие (1.15) можно переписать в виде:
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке. Если равенство (1.15) нарушено, то говорят, что при x = xo функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множествоR, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(xo)= f(0) не определено, поэтому в точке xo = 0 функция имеет разрыв. Функция f(x) называется непрерывной справа в точке xo, если
и непрерывной слева в точке xo, если
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева. Для того, чтобы функция была непрерывна в точке xo, например, справа, необходимо, во-первых, чтобы существовал конечный предел 1. Если 2. Если Например, функция y = ctg x при x® +0 имеет предел, равный +¥, значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x) в точках с целыми абсциссами имеет разрывы первого рода, или скачки. Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой. Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п. Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел e = 100 × (1 +1/10)10 » 259 (ден. ед.), 100 × (1+1/100)100 » 270 (ден. ед.), 100 × (1+1/1000)1000 » 271 (ден. ед.). При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
Пример 1. Пользуясь определением предела числовой последовательности, доказать, что последовательность xn =(n-1)/n имеет предел, равный 1. Решение. Нам надо доказать, что, какое бы e>0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство ½ xn -1 ½<e. Возьмем любое e >0. Так как ½ xn -1 ½=½(n+1)/n - 1½= 1/n, то для отыскания N достаточно решить неравенство 1/n<e. Отсюда n>1/e и, следовательно, за N можно принять целую часть от 1/e, N = E(1/e). Мы тем самым доказали, что Пример 2. Найти предел последовательности, заданной общим членом xn = Решение. Применим теорему о пределе суммы и найдем предел каждого слагаемого. При n ®¥ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему о пределе частного. Поэтому сначала преобразуем xn, разделив числитель и знаменатель первого слагаемого на n2, а второго на n. Затем, применяя теорему о пределе частного и о пределе суммы, найдем: xn = Пример 3. xn = Решение. Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания. Пример 4. Найти Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Преобразуем формулу общего члена:
Пример 5. Дана функция f(x)=21/x. Доказать, что Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { xn }, сходящуюся к 0, т.е. Пример 6. Доказать, что Решение. Пусть x1, x2,..., xn,... - последовательность, для которой Если xn= pn, то sin xn= sin pn = 0 при всех n и Пример 7. Найти Решение. Имеем: Пример 8. Вычислить Решение. Обозначим y=p-x. Тогда при x®p, y®0.Имеем: sin 3x = sin 3(p-y) = sin (3p-3y) = sin 3y. sin 4x = sin 4(p-y) = sin (4p-4y)= - sin 4y.
Пример 9. Найти Решение. Обозначим arcsin x=t. Тогда x=sin t и при x®0 t®0. Пример 10. Найти 1) Решение. 1. Применяя теорему 1 о пределе разности и произведения, находим предел знаменателя: Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе частного, получаем: 2. Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ¹ 2 равенство:
Так как
3. Числитель и знаменатель при x®¥ являются бесконечно большими функциями. Поэтому теорема о пределе частного непосредственно не применима. Разделим числитель и знаменатель на x2 и к полученной функции применим теорему о пределе частного:
Пример 11. Найти Решение. Здесь числитель и знаменатель стремятся к нулю: Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения
Пример 12. Найти Решение. 6.2. Применение пределов в экономических расчетах Сложные проценты В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов: S = P(1 + i)n. (1.16) Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n-го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем: P = Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна. В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году: S =P (1 + i/m) mn. Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m ®¥ имеем: `S = Поскольку При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d, тогда `S = Pe Сила роста d представляет собой номинальную ставку процентов при m®¥. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции. Потоки платежей. Финансовая рента Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами. Пример 13. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка - 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10 6 ´ 1,053 так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10 6 ´ 1,052, так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10 6 ´ 1,053; 10 6 ´ 1,052; 10 6 ´ 1,05; 10 6. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S - наращенная сумма ренты, R - размер члена ренты, R (1 + i)n - 1, R (1 + i)n - 2,..., R (1 + i), R. Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R´((1 + i)n - 1)/((1 + i) - 1) = Величина a n; i = (1 - (1 + i) - n)/ i называется коэффициентом приведения ренты. Коэффициент приведения ренты при n ®¥ показывает, во сколько раз современная величина ренты больше ее члена:
Пример 14. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено - она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из Коэффициент приведения для вечной ренты a n; i ® 1/i, откуда A = R/i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов. Производная 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или xn ® a.
или xn ® a.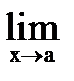 f(x) = A. (1.3)
f(x) = A. (1.3)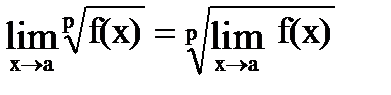 ;
;
 = 1,
= 1, 
 = 1, a = const, a >0,
= 1, a = const, a >0,
 = 1, (1.10)
= 1, (1.10) (1 + a)1/ a = e, (1.11)
(1 + a)1/ a = e, (1.11) = logc e, (1.12)
= logc e, (1.12) (aa - 1)/a = ln a, (1.13)
(aa - 1)/a = ln a, (1.13) = 1.
= 1. и
и 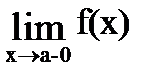 называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы
называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы  =
=  .
.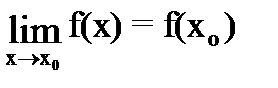 . (1.15)
. (1.15) ,
, ,
, .
. , а во-вторых, чтобы этот предел был равен f(xo). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
, а во-вторых, чтобы этот предел был равен f(xo). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.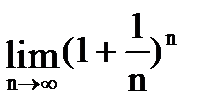 . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)3 »237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)3 »237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится: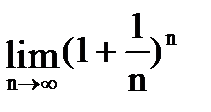 = e.
= e. xn = 1.
xn = 1.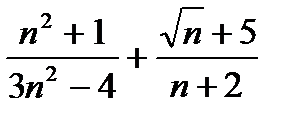 .
.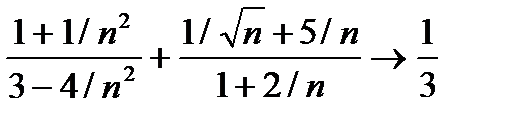 .
. . Найти
. Найти  .
. ).
).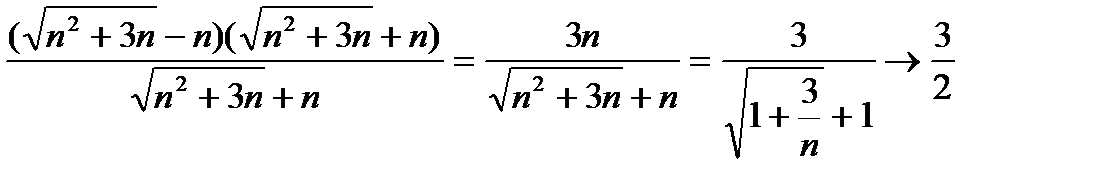 .
. не существует.
не существует. для разных последовательностей ведет себя по-разному. Пусть xn = 1/n. Очевидно, что
для разных последовательностей ведет себя по-разному. Пусть xn = 1/n. Очевидно, что  sin x не существует.
sin x не существует. .
. . Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим 5
. Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим 5 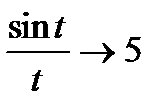 .
.
 .
. .
.
 .
. =
=  .
.
 ; 2)
; 2) 
 .
. .
. .
. (x+1) ¹ 0, то, по теореме о пределе частного, найдем
(x+1) ¹ 0, то, по теореме о пределе частного, найдем .
.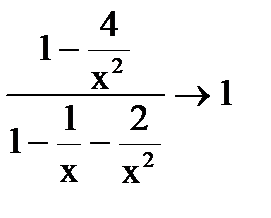 .
.
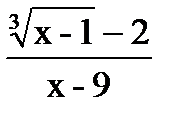 .
. , x-9®0, т.е. имеем неопределенность вида
, x-9®0, т.е. имеем неопределенность вида 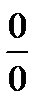 .
. , получим
, получим .
.
 .
. .
. Þ
Þ  P (1 + i/m) mn = P
P (1 + i/m) mn = P  .
.