
|
|
Проверка общей устойчивости подпорной стенки12 1. Привести сдвигающийся грунтовый массив к однородному с плотностью грунта, находящегося во взвешенном состоянии(p˳=p₂=p₃=1 т/м³).Для этого интенсивность нагрузки над расчетным уровнем воды приводят к высоте
Абсолютные координаты X˳=xH=0,31*10,5=3,25; Y˳=yH=3,6, Где x и y – относительные координаты центра «О», определяемые по таблице № 5. Таблица 5 Относительные координаты центра поверхности скольжения
∆h-превышение эпюры приведенных нагрузок над отметкой территории порта. Радиус поверхности скольжения определяют проведением ее через низ шпунтовой стенки. Всю сдвигающуюся призму грунта разбиваем на полоски равной ширины b=0,1*R=0,1*19=1,9 м Таблица 6 Результаты вычислений
L=0.0175*B*R=0.0175*88*19=29.26, м 4. Определение координат x1,x2,x1̽̽,x2̽̽ полосовых нагрузок
Координаты x1,x2,x1̽̽,x2̽̽определены согласно исходным данным в долях от от ширины активной зоны «В» Ширину активной зоны «В», в пределах которой нагрузку нормируют по условию прочности и устойчивости подпорного сооружения, можно вычислить по формуле
Где
Полученное значение «B» округляем до целого числа в большую сторону В=28,18≈29 м Определяем числовые значения координат полос загружения х1,х2 ,
Учет влияния полосовой нагрузки на шпунтовую стенку
Учет влияния полосовой нагрузки на шпунтовую стенку
5. Определение допускаемой нагрузки [q(x1,x2)] Допускаемой нагрузкой [ q ( ΔM[q(x1, x2)] = ΔM(q0) ΔRa[q (x1, x2)] = ΔRa(q0) Где ΔM[q(x1, x2)] и ΔRa[q (x1, x2)] – приращения максимального изгибающего момента в шпунтовой стенке и усилия в анкерной тяге от нагрузки q (x1, x2); ΔM(q0) и ΔRa(q0) – то же. От проектной нагрузки q0. Искомые значения вычисляются по формулам: ΔM[q0(O, B)] = Mmaxq(0) – Mmax0 = 244,8 – 142,8 = 102 кНм ΔRa[q0(O, B)] = Ra q(0) – Ra0 = 328,4 – 164,2 = 164,2 кН /м Где Mmaxq(0) – максимальный изгибающий момент в шпунтовой стенке при наличии нагрузки q0 , кНм/м Mmax = ƞ∙y1 = 300∙1,2 = 360 кНм Mmaxq(0)= Mmax*k₁= 360*0,68=244,8 кН/м. Ra q(0) – усилие в анкерной тяге при наличии проектной нагрузки q˳ (при d=1 м), кН/м
Mmax0 и Ra0 соответственно, то же ,но при отсутствии полезных нагрузок, кНм/м, кН/м. Mmax = ƞ∙y1=300*0,7=210 Mmaxq(0)= Mmax*k₁= 210*0,68=142,8 кН/м.
Приращения усилий в элементах больверка ΔM[q(x1, x2)] и ΔRa[q (x1, x2)] от нагрузки q(x1, x2) получаем по формулам: ΔM[q(x1, x2)] = Mmax[q(x1, x2)] – Mmax0 = 318.2 – 142.8= 175.4 кНм ΔRa[q (x1, x2)] = Ra[q(x1, x2)] – Ra0 = 252.6 – 164.2= 88.4 кН/м Где Mmax[q(x1, x2)] и Ra[q(x1, x2)] –максимальный изгибающий момент и усилие в анкерной тяге при наличии нагрузки q(x1, x2)., кНм/м; , кН/м; Mmax = ƞ∙y1 = 300∙1,3 = 468 кНм Mmax[q(x1, x2)]= Mmax*k₁= 468*0,68=318,2 кН/м.
Ra[q(x1, x2)] = Получив приращения усилий в элементах больверка по формулам .Строим графики линейных зависимостей ΔM[q(x1, x2)] и ΔRa[q (x1, x2)] от q(x1, x2) ( Рис. .) Определяем значения нагрузок q [(x1, x2), М] и q[ (x1, x2), Ra], лимитируемые, соответственно , шпунтовой стенкой и анкерной тягой; Меньшая из нагрузок является допускаемой нагрузкой для полосы с координатами x1 и x2 (на Рис. это q[ (x1, x2), М], q[ (x1, x2), М] = 46 кПа Определение эквивалентной равномерно распределенной нагрузки
Определяем приращение изгибающего момента в шпунтовой стенке
Где Mmax[q( Mmax = ƞ∙y1 = 300*0,8 = 240 кНм Mmax[q(
Ra[q(x1, x2)] = 7.Определение допустимой эксплуатационной нагрузки q(х1,х2) Используя общую формулу находим допустимую эксплуатационную нагрузку
Где
Допустимая эксплуатационная нагрузка: qэкв= 76кПа

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 эквивалентного слоя грунта с плотностью p˳=1 т/м³.
эквивалентного слоя грунта с плотностью p˳=1 т/м³.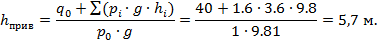
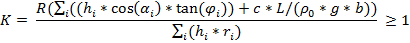
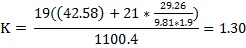
 (15)
(15) – мощности i- тых слоёв грунта от отметки поверхности грунта засыпки до отметки, на которой изгибающий момент в шпунтовой стенке
– мощности i- тых слоёв грунта от отметки поверхности грунта засыпки до отметки, на которой изгибающий момент в шпунтовой стенке  достигает наибольшего значения (рис2,д)
достигает наибольшего значения (рис2,д)


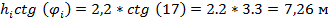
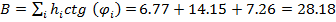 м
м и показывают на рис.4 положение фактической q*(
и показывают на рис.4 положение фактической q*(  =0,15*29=4,4 м
=0,15*29=4,4 м =0,4*29=11,6 м
=0,4*29=11,6 м =0,6*29=17,4 м
=0,6*29=17,4 м =0,75*29=21,8 м
=0,75*29=21,8 м кПа
кПа кПа
кПа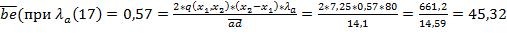 кПа
кПа кПа
кПа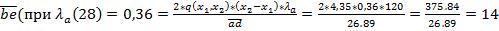 кПа
кПа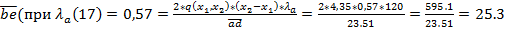 кПа
кПа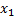 ,
, 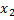 )] на полосе в активной зоне с координатами
)] на полосе в активной зоне с координатами  и
и  . Выражается равенствами
. Выражается равенствами a=260 кН/м
a=260 кН/м a*k₂*d=260*1,263*1=328,4 Кн/м
a*k₂*d=260*1,263*1=328,4 Кн/м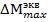 и усилия в анкерной тяге
и усилия в анкерной тяге 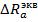 от полезных нагрузок.
от полезных нагрузок.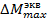 [q(
[q( 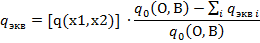
 = 76 кПа
= 76 кПа =80 кПа
=80 кПа = 40 кПа
= 40 кПа -снято с графика
-снято с графика