
|
|
Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам в идеальном газе.12 Термодинамика Первое начало термодинамики. Правило знаков для теплоты и работы. Формула для вычисления работы идеального газа. Работа газа в изобарном и в изотермическом процессе.
Уравнение (1) выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (1) в дифференциальной форме будет иметь вид
или в более корректной форме
где dU — бесконечно малое изменение (приращение) внутренней энергии системы, δA — элементарная работа, δQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а δA и δQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (2). Из формулы (1) мы видим, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии равно нулю: ΔU=0. Тогда, согласно первому началу термодинамики,
т. е. вечный двигатель первого рода — периодически действующий двигатель, совершающий бoльшую работу, чем сообщенная ему извне энергия, — невозможен (одна из формулировок первого начала термодинамики). Правило знаков:
– изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы. Работа, совершаемая при изменении объема газа Работа при изобарическом процессе
Работа при изотермическом процессе
Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам в идеальном газе. 1. Изохорический процесс (V = const). Работа в этом процессе равна нулю. Процесс сводится к теплообмену системы с окружающей средой. Первый закон термодинамики при этом условии принимает вид:
количество теплоты, полученное системой, если она представляет собой один моль идеального газа, равно
Поскольку CV > 0 для всех веществ, то знаки Q и ΔТ совпадают. При Q > 0 (энергия подводится к системе) температура системы повышается, т.е. ΔТ > 0, при Q < 0 система охлаждается, т.е. ΔТ < 0. Если в состав системы входит ν молей идеального газа, то равенство (4.26) представляется в виде:
где m – масса газа, μ – его молекулярная масса.
2. Изобарический процесс (Р = const). На основании определения теплоемкости количество теплоты Q, подведенное к системе в изобарном процессе, для одного моля идеального газа равно:
Поскольку для любой системы CP > 0, то при Q > 0 (система получает энергию извне) ΔТ > 0 и Т2 > T1, система нагревается. При Q < 0 (система отдает энергию окружающей среде) ΔТ < 0, Т2 < T1, система охлаждается. Уравнение (4.28) для ν молей идеального газа записывается в виде:
Найдем работу, которую совершает система в изобарическом процессе, переходя из состояния 1 в состояние 2. Начальное и конечное состояния системы описываются уравнениями
из которых следует
Обобщение равенства (4.30) для случая молей в системе приводит к результату:
3. Изотермический процесс. При изотермическом процессе температура системы не изменяется (ΔТ = 0), а, следовательно, ее внутренняя энергия, являясь для идеального газа только функцией температуры, остается постоянной, то есть ее изменение ΔU = 0. Это значит, что сообщаемое системе количество теплоты идет на совершение работы.
Найдем работу расширения моля идеального газа в изотермическом процессе. Изотерма в координатах Р – V представляется гиперболой (рис. 4.9). Как уже было рассмотрено ранее, работу расширения газа от начального объема V1 до V2 можно найти, используя равенство :
Давление моля идеального газа, как следует из уравнения состояния, равно
Очевидно, что чем меньшие интервалы изменения объема ΔVi выбираются для вычисления работы, тем точнее будет получено ее значение. Предельный переход в соотношении (4.32) приводит к выражению:
где V1 и V2 – объемы, занимаемые системой соответственно в начальном и конечном состояниях. Обобщая формулу (4.33) на случай системы, содержащей ν молей газа, получаем равенство:
Пользуясь уравнением изотермического процесса (PV = const), равенство (4.34) можно представить через другие параметры состояния системы:
где Р1 и Р2 – давление газа в начальном и конечном состояниях. 4. Адиабатический процесс. Адиабатический процесс – процесс, идущий без теплообмена с окружающей средой. Это значит, что система должна быть теплоизолирована, либо процесс должен протекать так быстро, что за время процесса не происходит теплообмена системы с окружающей средой. Условие адиабатичности процесса означает, что Q = 0. Уравнение первого закона термодинамики для адиабатического процесса принимает вид:
Из последнего соотношения следует, что А = – ΔU и для одного моля идеального газа равно
Из (4.37) очевидно, что если адиабатически изолированная система подвергается сжатию (внешние силы совершают над системой работу, поэтому работа отрицательна), то ΔU > 0. Это означает, что адиабатическое сжатие идеального газа приводит к повышению его температуры. Напротив, адиабатическое расширение идеального газа (работа совершается самой системой, поэтому она положительна) может происходить только за счет уменьшения его внутренней энергии (ΔU < 0), поэтому температура газа при его адиабатическом расширении должна понижаться. Все рассмотренные выше процессы могут быть представлены одним уравнением – уравнением политропического процесса. Политропический процесс – это процесс, идущий с постоянной теплоемкостью. Уравнение политропического процесса имеет вид
где 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)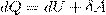

 если тепло передаётся от окружающей среды данной системе,
если тепло передаётся от окружающей среды данной системе,  и
и  если система производит работу над окружающими телами, при этом
если система производит работу над окружающими телами, при этом 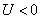 . Учитывая правило знаков, первое начало термодинамики можно записать в виде:
. Учитывая правило знаков, первое начало термодинамики можно записать в виде: ,
,
 ,
,  .
.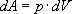 , но р = const , поэтому
, но р = const , поэтому 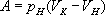
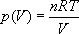 , поэтому
, поэтому 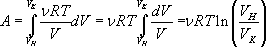 .
.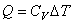 .
.
 ,
,
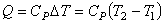 .
.
 .
.
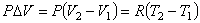 .
.
 .
.
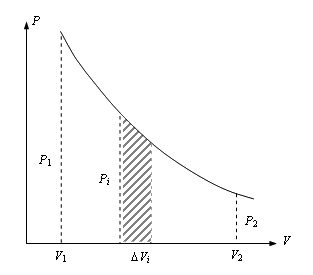 Рис. 4.9
Рис. 4.9
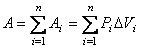 .
.
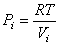 .
.
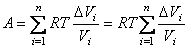 .
.
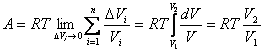 ,
,
 .
.
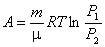 ,
,
 .
.
 .
.
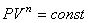 ,
,
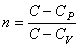 – показатель политропы.
– показатель политропы.