
|
|
Уравнение электромагнитного поля. Первая пара уравнений Максвелла.12 Сокращение масштабов, собственное время. Из правил Лоренца вытекает, что свойства движущихся часов и линеек отличаются от свойств покоящихся.
Какова будет длина линейки в движущейся системе? Пусть линейка покоится относительно K', то есть она движется относительно системы K.
Используем преобразование Лоренца
Полученный эффект называется эффектом сокращения пространства. Движущийся предмет выглядит более коротким. Если линейка ориентирована перпендикулярно, то ее длина не меняется. В случае трехмерного объекта со сторонами
Объем объекта при переходе в движущуюся систему отсчета изменяется (уменьшается).
Р/м свойства движущихся часов. Имеются часы, которые покоятся относительно системы K', и измеряют в ней отрезок времени
Определим, какой промежуток времени прошел для наблюдателя, находящейся в K
Часы для покоящегося наблюдателя движутся быстрее, чем для движущегося. Собственное время является минимальным из всех времен. Р/м случай неравномерного движения
Разбить движение объекта на множество интервалов - таких, на которых скорость не меняется. Введем понятие воображаемой системы отсчета (сопутствующей) - система отсчета, которая движется вместе с телом, относительно которого объект всегда покоится. Каждая "система" имеет смысл только на бесконечно малых промежутках времени dt, то есть на таких малых, что на каждом отрезке движения за время dt скорость можно считать постоянной.
- собственное время по часам движущегося наблюдателя.
Преобразование скорости и аберрации света Закон сохранения скоростей:
Для движущейся системы отсчёта Определим математический смысл поставленной задачи.
Для наблюдателя в системе K’.
(1) Здесь (2) формулы преобразования скоростей. K↔K’ (x, y, z) ↔ (x’, y’, z’) – для обратного преобразования (2)
Здесь (3) – формулы обратного преобразования. Аберрации света.
ф = ф’ Следовательно, поворота вокруг оси x не происходит.
В релятивистском случае угол Ѳ немного меньше, то есть происходит смещение векторов скорости в направлении движения. Представим свет как поток частиц, каждая из которых движется со скоростью света. Мы знаем, что скорость света одинакова во всех системах отсчёта. Изменение скорости света происходит за счёт изменения угла Ѳ.
Геометрический смысл преобразования Лоренца. Любая точка в 4-хмерном мире характеризуется четырьмя числами (x,y,z,t). При описании событий мы используем числовые значения. Мировая линия – совокупность последовательных событий.
При переходе в другую систему отсчета квадрат расстояния не меняется.
Введем
В плоскости xτ преобразование Лоренца соответствует повороту системы координат на псевдо-угол ψ.
Переход от покоящейся к движущейся системе отсчета в 4-хмерном мире соответствует повороту. При повороте не изменяется и расстояние между 2-мя точками (событиями).
Если рассматривать события 1 и 2, то расстояние между ними не изменяется.
Рассмотрим релятивистские эффекты 1) Понятие одновременности событий
В новой системе отсчета события уже не одновременные 2) Эффект сокращения длины
3) Эффект замедления времени
4) Если скорость относительного движения сонаправлена с осью y, то такому движению будут соответствовать поворот оуτ. Результат 2-х последовательных переходов – 2 поворота плоскостей. Результат зависит от порядка выполнения перехода. Преобразование Лоренца некоммутативное. Исключение: составное движение производится вдоль одной оси. _______________________________________ Уравнение электромагнитного поля. Первая пара уравнений Максвелла.
Уравнение электромагнитного поля
Поток вектора В через любую замкнутую поверхность равен нулю

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|






 - собственная длина линейки - это длина, измеренная в той системе отсчета, относительно которой объект покоится, при чем зависит она только от свойств линейки.
- собственная длина линейки - это длина, измеренная в той системе отсчета, относительно которой объект покоится, при чем зависит она только от свойств линейки. , он имеет объемы:
, он имеет объемы:



 - собственный объем - объем объекта в системе, относительно которой объект покоится.
- собственный объем - объем объекта в системе, относительно которой объект покоится. :
:




 - собственное время - промежуток времени, измеренный в системе, где часы покоятся.
- собственное время - промежуток времени, измеренный в системе, где часы покоятся.
 - собственное время для объекта.
- собственное время для объекта.

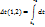

 - инвариантная величина: произведение трехмерного объема на временной интервал остается постоянным в любой системе отсчета. Четырехмерный объем так же сохраняется.
- инвариантная величина: произведение трехмерного объема на временной интервал остается постоянным в любой системе отсчета. Четырехмерный объем так же сохраняется.

 =
= 
 =
= 
 =
=  =
= 
 =
=  =
= 









 =
= 
 =
= 
 <<
<< 














 , тогда:
, тогда:







 ;
; 

 ;
; 





 – поле соленоида
– поле соленоида


