Теоремы о сходящихся последовательностях
| Теорема о сумме, разности и произведении сходящихся последовательностей
| Если последовательности 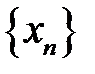 и и 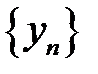 являются сходящимися, то есть имеют конечные пределы: являются сходящимися, то есть имеют конечные пределы:  и и 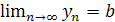 , ,  и и 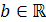 , то сходящимися являются их сумма, разность и произведение, при этом
справедливы следующие равенства: , то сходящимися являются их сумма, разность и произведение, при этом
справедливы следующие равенства:
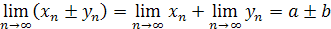

|
w Для доказательства используем признак сходящейся последовательности и свойства бесконечно малых последовательностей:
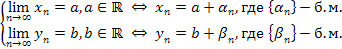
1) 
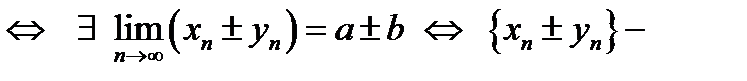 сходящаяся последовательность; сходящаяся последовательность;
2) 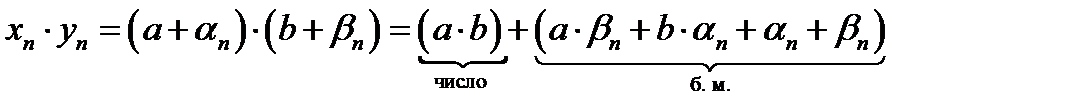
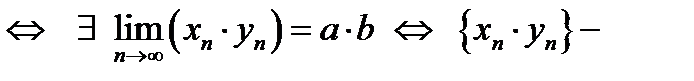 сходящаяся последовательность. v сходящаяся последовательность. v
Замечания
1. В качестве следствия из теоремы о пределе произведения получаем, что если одна из перемножаемых последовательностей является стационарной, например, 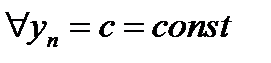 , то , то 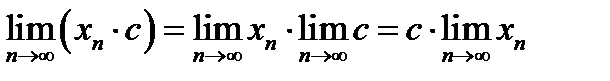 , ,
так как предел постоянной равен этой постоянной. Поэтому следствие можно сформулировать так:
постоянный множитель можно выносить за знак предела последовательности.
2. Теоремы о пределе суммы и о пределе произведения сходящихся последовательностей распространяются на любое конечное число слагаемых или сомножителей:
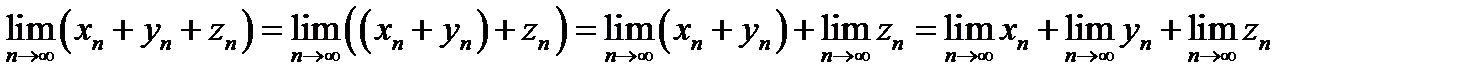 ; ;  . .
| Теорема о пределе дроби
| Если последовательность 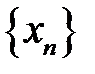 – сходится, последовательность – сходится, последовательность 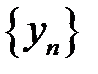 – сходится, но при этом не является бесконечно малой и – сходится, но при этом не является бесконечно малой и 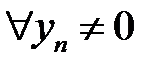 : :
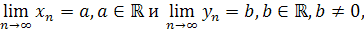 то сходящуюся последовательность образуют дроби
то сходящуюся последовательность образуют дроби  , при этом справедлива следующая формула: , при этом справедлива следующая формула:
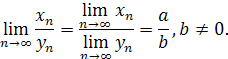
|
wДля доказательства используем признак сходящейся последовательности:
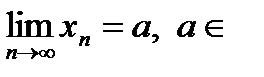 ℝ ℝ 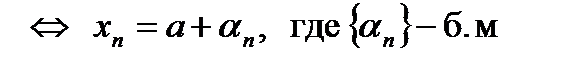 .; .;
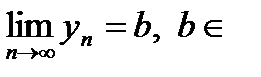 ℝ ℝ 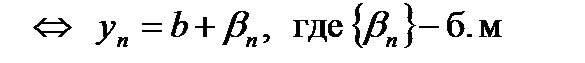 . .
Дроби  можно образовать, так как можно образовать, так как 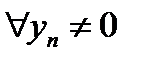 , и представить в следующем виде: , и представить в следующем виде:
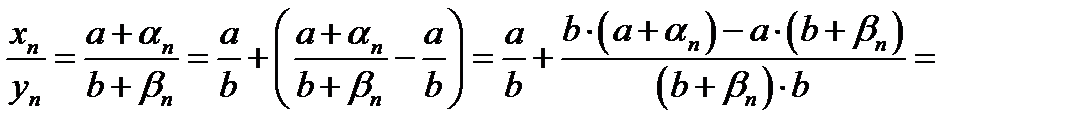
 . .
Поработаем с последовательностью 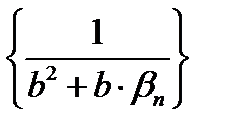 : :
 следовательно, следовательно,  ограниченная как всякая сходящаяся последовательность, но не является бесконечно малой (так как ограниченная как всякая сходящаяся последовательность, но не является бесконечно малой (так как 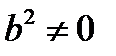 ); при этом при достаточно больших номерах n величины ); при этом при достаточно больших номерах n величины 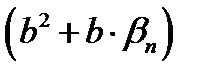 являются положительными, так как становятся сколь угодно близкими к числу являются положительными, так как становятся сколь угодно близкими к числу  , поэтому обратные им величины , поэтому обратные им величины 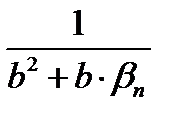 также являются ограниченными. также являются ограниченными.
Теперь можно сделать вывод о том, что величины 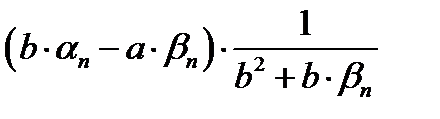 образуют бесконечно малую последовательность (по теореме о произведении бесконечно малой и ограниченной последовательностей). образуют бесконечно малую последовательность (по теореме о произведении бесконечно малой и ограниченной последовательностей).
Таким образом, доказано, что
 . v . v
Практическое вычисление пределов. Понятие о неопределенностях
Рассмотрим примеры вычисления пределов с использованием доказанных теорем о бесконечно малых, бесконечно больших, ограниченных и сходящихся последовательностях:
1) 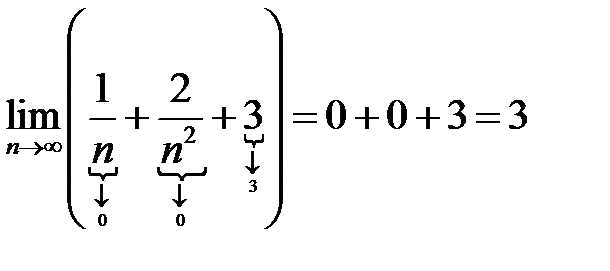 , по теореме о пределе суммы сходящихся последовательностей; , по теореме о пределе суммы сходящихся последовательностей;
2)  , по теореме о сумме двух бесконечно больших одного знака; , по теореме о сумме двух бесконечно больших одного знака;
3)  , по теореме о произведении бесконечно большой на ограниченную последовательность, так как последовательность , по теореме о произведении бесконечно большой на ограниченную последовательность, так как последовательность 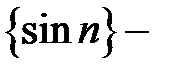 ограниченная, но не является бесконечно малой и ограниченная, но не является бесконечно малой и  ; ;
4) 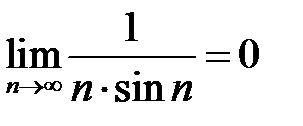 , по теореме о связи бесконечно большой и бесконечно малой; , по теореме о связи бесконечно большой и бесконечно малой;
5) 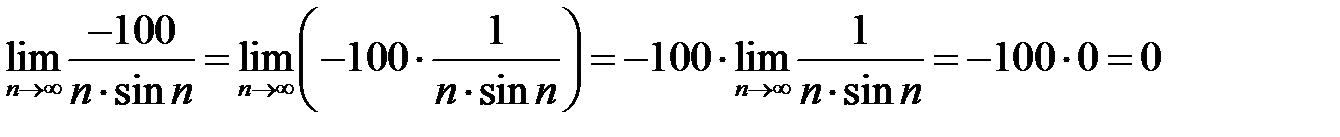 , так как постоянный множитель можно выносить за знак предела; , так как постоянный множитель можно выносить за знак предела;
6)  , по теореме о произведении бесконечно малой и ограниченной последовательностей. , по теореме о произведении бесконечно малой и ограниченной последовательностей.
Если заданный предел нельзя вычислить ни по одной из теорем о сходящихся, о бесконечно малых, о бесконечно больших и ограниченных последовательностях, то говорят, что в этом пределе имеется неопределенность, и указывают её тип: 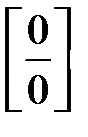 , ,  , , 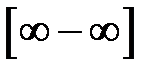 , ,  и другие. Чтобы вычислить такой предел, нужно неопределенность раскрыть; смысл этой процедуры состоит в том, чтобы сделать тождественное преобразование выражения, стоящего под пределом, так, чтобы неопределенность исчезла, и предел можно было вычислить по одной из рассмотренных теорем. и другие. Чтобы вычислить такой предел, нужно неопределенность раскрыть; смысл этой процедуры состоит в том, чтобы сделать тождественное преобразование выражения, стоящего под пределом, так, чтобы неопределенность исчезла, и предел можно было вычислить по одной из рассмотренных теорем.
Примеры (раскрытие неопределенностей)
1) 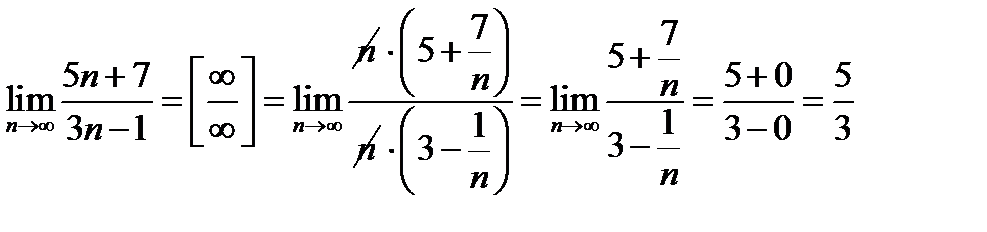 , окончательно предел вычисляется по теореме о пределе дроби; , окончательно предел вычисляется по теореме о пределе дроби;
2) 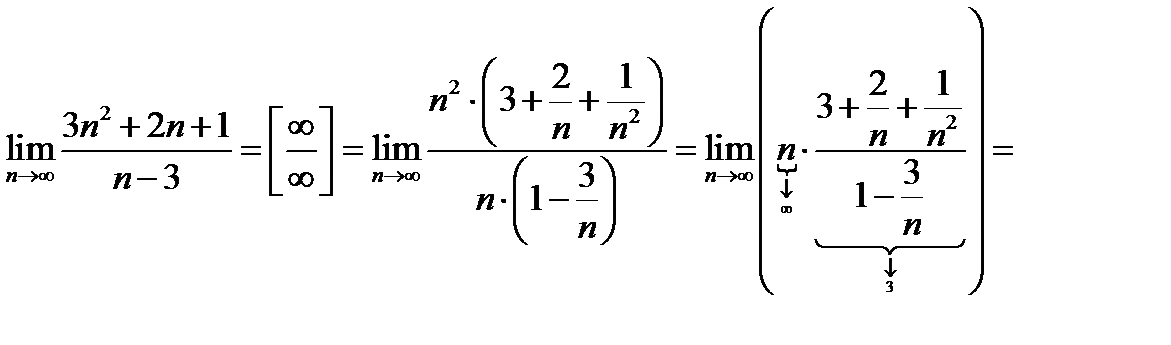
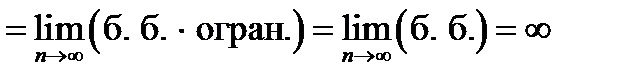 , при вычислении предела были использованы теорема о пределе дроби, об ограниченности сходящейся последовательности и о произведении бесконечно большой на ограниченную последовательность, не являющуюся бесконечно малой; , при вычислении предела были использованы теорема о пределе дроби, об ограниченности сходящейся последовательности и о произведении бесконечно большой на ограниченную последовательность, не являющуюся бесконечно малой;
3) 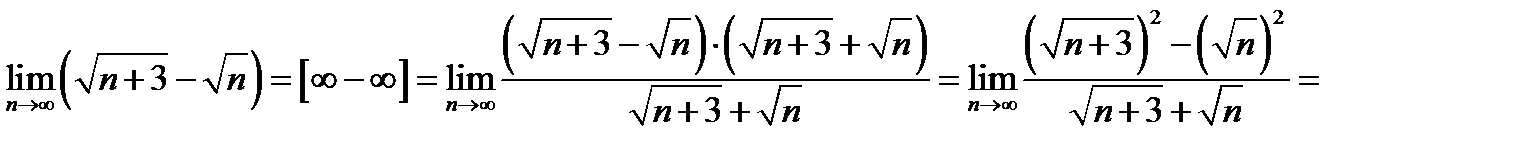
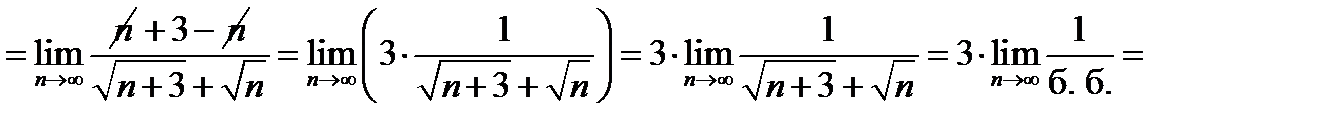
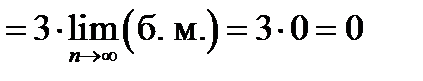 , при вычислении использованы теоремы о сумме двух бесконечно больших одного знака, о связи бесконечно большой с бесконечно малой, постоянный множитель вынесен за знак предела. , при вычислении использованы теоремы о сумме двух бесконечно больших одного знака, о связи бесконечно большой с бесконечно малой, постоянный множитель вынесен за знак предела.
3.6. Упражнения для самостоятельной работы
1.Вычислите следующие пределы, используя теоремы о бесконечно малых, бесконечно больших, ограниченных и сходящихся последовательностях:
1) 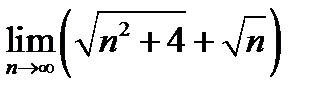 ; 2) ; 2)  ; 3) ; 3)  ; ;
4) 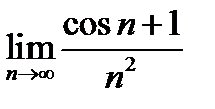 ; 5) ; 5)  ; ;
6)  ; 7) ; 7) 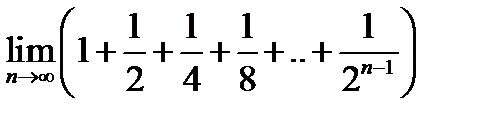 . .
2. Вычислите следующие пределы, раскрыв имеющиеся в них неопределенности:
1) 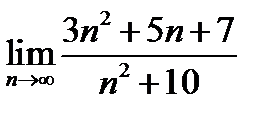 ; 2) ; 2) 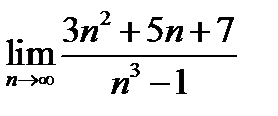 ; 3) ; 3) 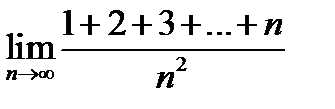 ; ;
4)  ; 5) ; 5) 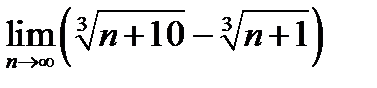 ; 6) ; 6) 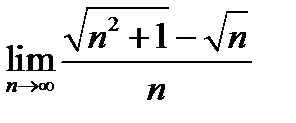 . .
Ответы к упражнениям для самостоятельной работы
1.1) 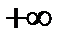 ; 2) 0; 3) ; 2) 0; 3)  ; 4) 0; 5) ; 4) 0; 5) 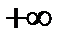 ; 6) ; 6) 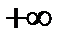 ; 7)2; ; 7)2;
2. 1) 3; 2) 0; 3) 0,5; 4)  ; 5) 0; 6) 1. ; 5) 0; 6) 1.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


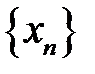 и
и 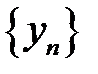 являются сходящимися, то есть имеют конечные пределы:
являются сходящимися, то есть имеют конечные пределы:  и
и 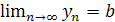 ,
,  и
и 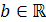 , то сходящимися являются их сумма, разность и произведение, при этом
справедливы следующие равенства:
, то сходящимися являются их сумма, разность и произведение, при этом
справедливы следующие равенства:
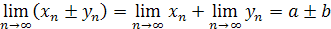

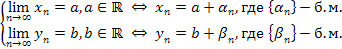

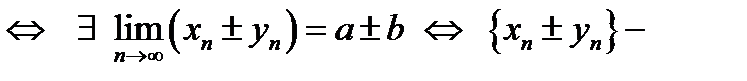 сходящаяся последовательность;
сходящаяся последовательность;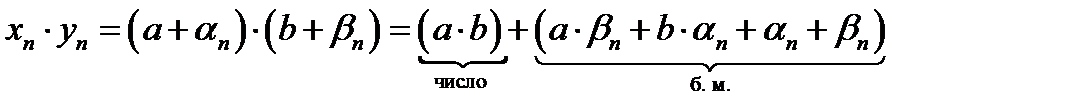
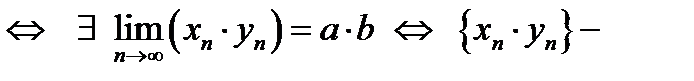 сходящаяся последовательность. v
сходящаяся последовательность. v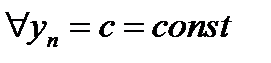 , то
, то 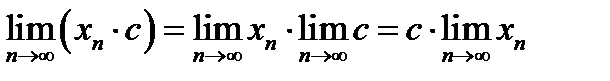 ,
,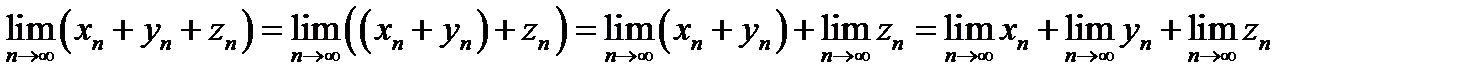 ;
;  .
. – сходится, но при этом не является бесконечно малой и
– сходится, но при этом не является бесконечно малой и 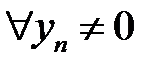 :
:
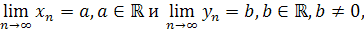 то сходящуюся последовательность образуют дроби
то сходящуюся последовательность образуют дроби  , при этом справедлива следующая формула:
, при этом справедлива следующая формула:
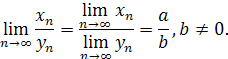
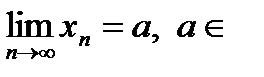 ℝ
ℝ 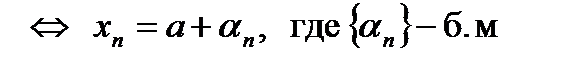 .;
.;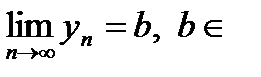 ℝ
ℝ 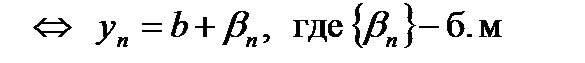 .
. можно образовать, так как
можно образовать, так как 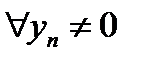 , и представить в следующем виде:
, и представить в следующем виде: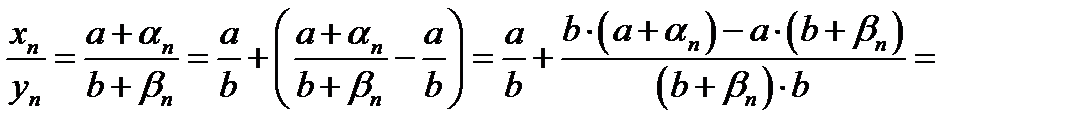
 .
.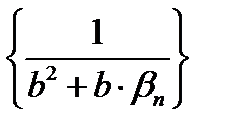 :
: следовательно,
следовательно,  ограниченная как всякая сходящаяся последовательность, но не является бесконечно малой (так как
ограниченная как всякая сходящаяся последовательность, но не является бесконечно малой (так как 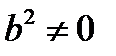 ); при этом при достаточно больших номерах n величины
); при этом при достаточно больших номерах n величины 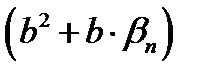 являются положительными, так как становятся сколь угодно близкими к числу
являются положительными, так как становятся сколь угодно близкими к числу  , поэтому обратные им величины
, поэтому обратные им величины 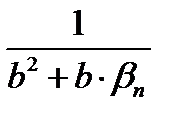 также являются ограниченными.
также являются ограниченными.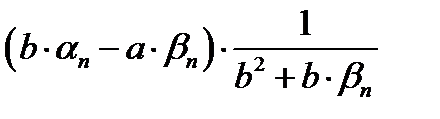 образуют бесконечно малую последовательность (по теореме о произведении бесконечно малой и ограниченной последовательностей).
образуют бесконечно малую последовательность (по теореме о произведении бесконечно малой и ограниченной последовательностей). . v
. v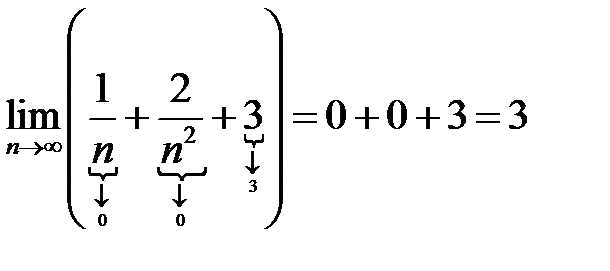 , по теореме о пределе суммы сходящихся последовательностей;
, по теореме о пределе суммы сходящихся последовательностей; , по теореме о сумме двух бесконечно больших одного знака;
, по теореме о сумме двух бесконечно больших одного знака; , по теореме о произведении бесконечно большой на ограниченную последовательность, так как последовательность
, по теореме о произведении бесконечно большой на ограниченную последовательность, так как последовательность  ограниченная, но не является бесконечно малой и
ограниченная, но не является бесконечно малой и  ;
;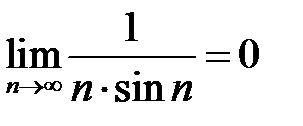 , по теореме о связи бесконечно большой и бесконечно малой;
, по теореме о связи бесконечно большой и бесконечно малой;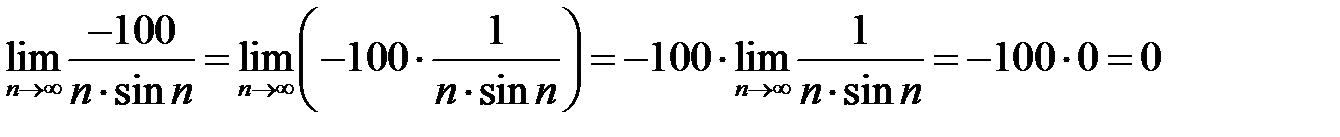 , так как постоянный множитель можно выносить за знак предела;
, так как постоянный множитель можно выносить за знак предела; , по теореме о произведении бесконечно малой и ограниченной последовательностей.
, по теореме о произведении бесконечно малой и ограниченной последовательностей.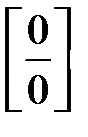 ,
,  ,
, 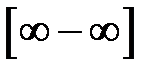 ,
,  и другие. Чтобы вычислить такой предел, нужно неопределенность раскрыть; смысл этой процедуры состоит в том, чтобы сделать тождественное преобразование выражения, стоящего под пределом, так, чтобы неопределенность исчезла, и предел можно было вычислить по одной из рассмотренных теорем.
и другие. Чтобы вычислить такой предел, нужно неопределенность раскрыть; смысл этой процедуры состоит в том, чтобы сделать тождественное преобразование выражения, стоящего под пределом, так, чтобы неопределенность исчезла, и предел можно было вычислить по одной из рассмотренных теорем.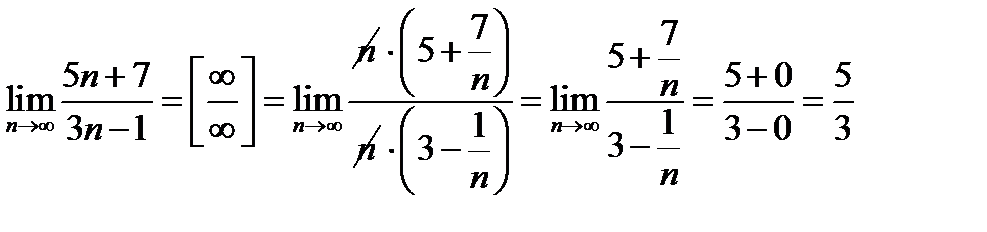 , окончательно предел вычисляется по теореме о пределе дроби;
, окончательно предел вычисляется по теореме о пределе дроби;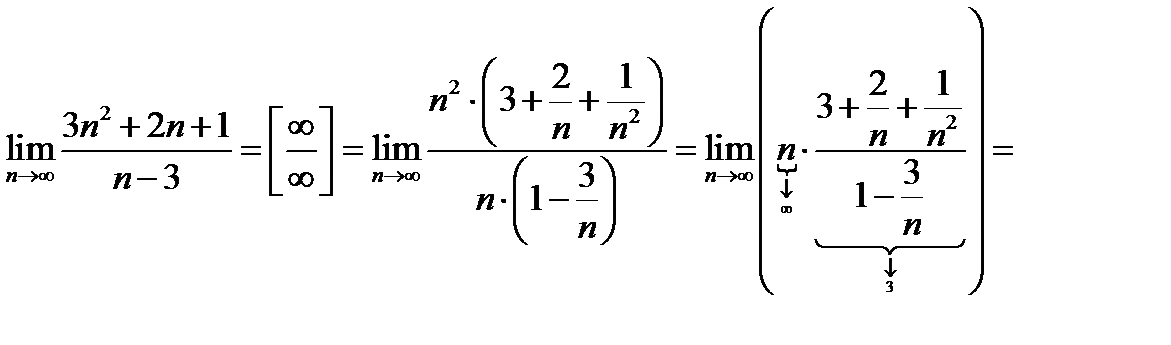
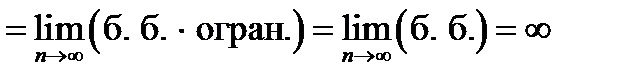 , при вычислении предела были использованы теорема о пределе дроби, об ограниченности сходящейся последовательности и о произведении бесконечно большой на ограниченную последовательность, не являющуюся бесконечно малой;
, при вычислении предела были использованы теорема о пределе дроби, об ограниченности сходящейся последовательности и о произведении бесконечно большой на ограниченную последовательность, не являющуюся бесконечно малой;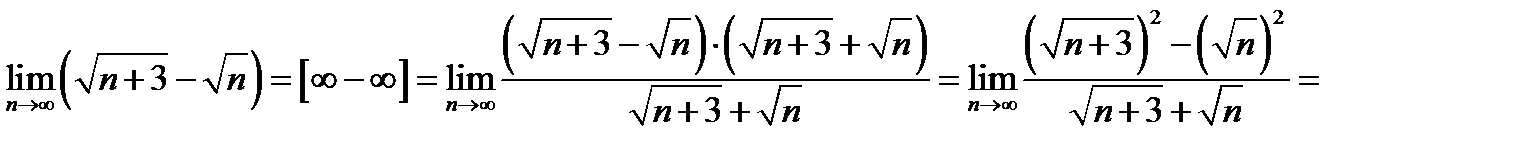
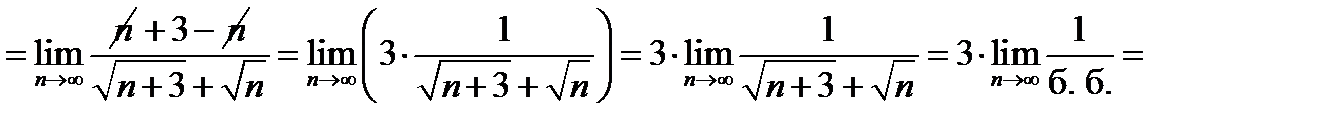
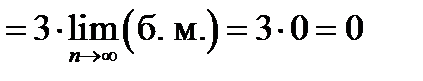 , при вычислении использованы теоремы о сумме двух бесконечно больших одного знака, о связи бесконечно большой с бесконечно малой, постоянный множитель вынесен за знак предела.
, при вычислении использованы теоремы о сумме двух бесконечно больших одного знака, о связи бесконечно большой с бесконечно малой, постоянный множитель вынесен за знак предела.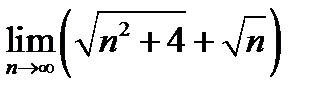 ; 2)
; 2)  ; 3)
; 3)  ;
;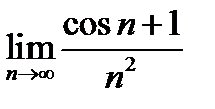 ; 5)
; 5)  ;
; ; 7)
; 7) 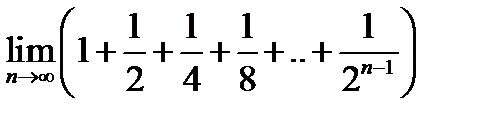 .
.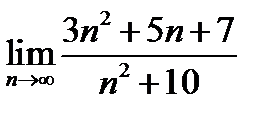 ; 2)
; 2) 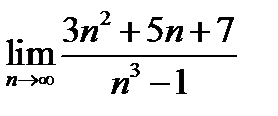 ; 3)
; 3) 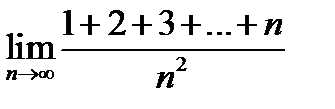 ;
; ; 5)
; 5) 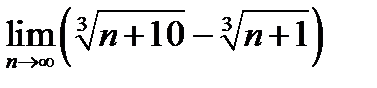 ; 6)
; 6) 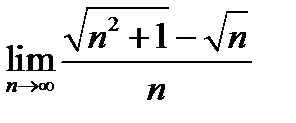 .
.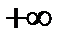 ; 2) 0; 3)
; 2) 0; 3)  ; 4) 0; 5)
; 4) 0; 5)