Примеры исследования последовательностей с точки зрения существования их предела
Оглавление
Введение. Ошибка! Закладка не определена.
Тема I. Предел последовательности. 4
§ 1. Определение предела последовательности. 4
§ 2. Основные свойства предела последовательности. Ограниченные последовательности. 14
§ 3. Основные теоремы о бесконечно малых, бесконечно больших и сходящихся последовательностях. 22
§ 4. Предел монотонной последовательности. Определение числа e. 32
§ 5. Подпоследовательности. Частичные пределы последовательности. Критерий Коши сходящейся последовательности. 37
§ 6. Предел функции: различные определения. 45
§ 7 Основные свойства пределов функций. Односторонние пределы.. 66
§ 8 Свойства бесконечно малых, бесконечно больших и локально ограниченных функций. Основные теоремы о функциях, имеющих конечный предел. ……………………………………………………………………………77
Введение
Тема I. Предел последовательности
Определение предела последовательности
Содержание
1.1. Числовая последовательность. 4
1.2. Предел последовательности. 6
1.3. Примеры исследования последовательностей с точки зрения существования их предела 9
1.4. Определение сходящейся, расходящейся, бесконечно большой или бесконечно малой последовательности. 12
1.5. Упражнения для самостоятельной работы.. 13
Числовая последовательность
| Определение числовой последовательности
| Числовой последовательностью  элементов некоторого множества элементов некоторого множества  ℝназывается отображение множества натуральных чисел ℕна это множество ℝназывается отображение множества натуральных чисел ℕна это множество  ℕ ℕ  . .
|
Из определения следует, что числовая последовательность есть функция натурального аргумента; множество ℕ задания этой функции является бесконечным и счетным; множество  значений функции может быть бесконечным счетным или конечным. значений функции может быть бесконечным счетным или конечным.
Числа  называются членами последовательности: называются членами последовательности:
 - первый член, - первый член,  - второй член, …, - второй член, …,  - -  -й член или общий член последовательности. -й член или общий член последовательности.
Будем далее называть числовую последовательность  просто последовательностью. просто последовательностью.
Пример (числовые последовательности)
1) 
2) 
3)  ; ;
4)  , т.е. , т.е.  . .
В случае, когда множество  состоит из одного элемента (то есть все члены последовательности одинаковы), состоит из одного элемента (то есть все члены последовательности одинаковы),  называется стационарной последовательностью. называется стационарной последовательностью.
Геометрическое изображение членов последовательности
Так как числовая последовательность  есть функция: есть функция:  , то для неё возможно изображение графиком, например, в декартовой прямоугольной системе координат (рис. 1). , то для неё возможно изображение графиком, например, в декартовой прямоугольной системе координат (рис. 1).

Рис. 1
График представляет собой дискретное множество точек плоскости и является избыточным изображением в том смысле, что значения аргумента  для любой последовательности для любой последовательности  всегда одинаковы, а интерес представляют только поведение значений функции всегда одинаковы, а интерес представляют только поведение значений функции  . Поэтому проще изображать последовательности как множество . Поэтому проще изображать последовательности как множество  точек на одной координатной оси (рис. 2). точек на одной координатной оси (рис. 2).

Рис. 2
Предел последовательности
| Определение предела последовательности
| Конечная или бесконечно удаленная точка а расширенной координатной прямой называется пределом числовой последовательности  , если какова бы ни была окрестность точки , если какова бы ни была окрестность точки  , она содержит все члены этой последовательности, начиная с некоторого номера , она содержит все члены этой последовательности, начиная с некоторого номера  . .
|
Обозначения:  , или , или  при при  , или , или  . .
Краткая запись определения предела:
(1)
Геометрическая иллюстрация и формальное описание конечного предела последовательности
Если  , то есть , то есть  – это конечная точка координатной прямой, то проиллюстрировать определение предела последовательности можно так, как на рис 3. – это конечная точка координатной прямой, то проиллюстрировать определение предела последовательности можно так, как на рис 3.

Рис. 3
При этом важно заметить следующие детали определения:
1) окрестность  назначается произвольно; вне выбранной окрестности точки назначается произвольно; вне выбранной окрестности точки  может находиться лишь конечное количество членов последовательности может находиться лишь конечное количество членов последовательности  , но внутри этой же окрестности всегда находится их бесконечное количество — все , но внутри этой же окрестности всегда находится их бесконечное количество — все  , начиная с некоторого номера , начиная с некоторого номера  ; ;
2) все числа  стремятся (приближаются) к числу стремятся (приближаются) к числу  в том смысле, что могут отличаться от него сколь угодно мало или, что то же, числа в том смысле, что могут отличаться от него сколь угодно мало или, что то же, числа  подходят к числу подходят к числу  сколь угодно близко; сколь угодно близко;
3) приближение чисел  к числу к числу  возможно как с обеих сторон, так и только с одной стороны: слева или справа; возможно как с обеих сторон, так и только с одной стороны: слева или справа;
4) не исключается, что значения некоторых  совпадают с числом совпадают с числом  . .
Если окрестность точки  описать как описать как  - окрестность, то нетрудно составить и проиллюстрировать формальное описание конечного предела последовательности (рис.4). - окрестность, то нетрудно составить и проиллюстрировать формальное описание конечного предела последовательности (рис.4).

Рис. 4
(2)
Записанное определение (2) прочитывается следующим образом:
число а называется пределом числовой последовательности  , если для любого положительного числа , если для любого положительного числа  , сколь малым бы оно ни было, можно указать номер , сколь малым бы оно ни было, можно указать номер  , зависящий от , зависящий от  , такой что выполняется неравенство , такой что выполняется неравенство  для всех номеров для всех номеров  , начиная с номера , начиная с номера  . .
Кратко смысл этого определения можно описать так:
если  , то это означает, что члены последовательности , то это означает, что члены последовательности  становятся сколь угодно близкими к числу становятся сколь угодно близкими к числу  , если брать номера , если брать номера  достаточно большими. достаточно большими.
Геометрическая иллюстрация и формальное описание предела последовательности, равного 
Если  , то иллюстрация к определению , то иллюстрация к определению  в соответствии с формальной записью (1) имеет вид, приведенный на рис. 5. в соответствии с формальной записью (1) имеет вид, приведенный на рис. 5.

Рис. 5
При этом также замечаем, что вне любой окрестности  может находиться лишь конечное число точек может находиться лишь конечное число точек  , внутри этой окрестности , внутри этой окрестности  всегда находится бесконечное количество точек всегда находится бесконечное количество точек  . Так как окрестность . Так как окрестность  может назначаться любая, то числа может назначаться любая, то числа  должны увеличиваться с возрастанием номера должны увеличиваться с возрастанием номера  и становиться сколь угодно большими. и становиться сколь угодно большими.
Если окрестность точки  описать как описать как  - окрестность: - окрестность:
 , то получится формальное описание предела, равного , то получится формальное описание предела, равного  , и его иллюстрация (рис. 6): , и его иллюстрация (рис. 6):

Рис. 6
Приводим краткое описание этого определения:
если  , то это означает, что члены последовательности , то это означает, что члены последовательности  становятся сколь угодно большими положительными, если брать их номера становятся сколь угодно большими положительными, если брать их номера  достаточно большими. достаточно большими.
Геометрическая иллюстрация и формальное описание предела последовательности, равного 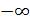
Если  , то иллюстрация и формальное описание приведены ниже, (рис.7) , то иллюстрация и формальное описание приведены ниже, (рис.7)

Рис.7
Краткое описание этого определения:
если  , то это означает, что члены последовательности , то это означает, что члены последовательности  становятся сколь угодно большими по модулю, но отрицательными, если брать их номера становятся сколь угодно большими по модулю, но отрицательными, если брать их номера  достаточно большими. достаточно большими.
Геометрическая иллюстрация и формальное описание предела последовательности, равного 
Если  , то на рис.8 приведена иллюстрация и далее формальное определение: , то на рис.8 приведена иллюстрация и далее формальное определение:

Рис.8
Краткий смысл этого определения:
если  , то это означает, что члены последовательности , то это означает, что члены последовательности  становятся сколь угодно большими по модулю, если брать их номера становятся сколь угодно большими по модулю, если брать их номера  достаточно большими. достаточно большими.
Примеры исследования последовательностей с точки зрения существования их предела
Рассмотрим несколько последовательностей, имеющих различное предельное поведение своих членов при  . При этом полезно наблюдать расположение членов каждой последовательности на координатной оси. . При этом полезно наблюдать расположение членов каждой последовательности на координатной оси.

Если отметить эти числа  на координатной оси (рис. 9), то нетрудно предположить, что на координатной оси (рис. 9), то нетрудно предположить, что  , так как в любую окрестность числа 0 попадает в бесконечное множество чисел , так как в любую окрестность числа 0 попадает в бесконечное множество чисел  , вернее, попадают все , вернее, попадают все  , начиная с некоторого номера. , начиная с некоторого номера.

Рис. 9
Докажем строго, что  , пользуясь записью определения (2): , пользуясь записью определения (2):
 при при  . .
Действительно, зафиксируем произвольное малое число  и найдем номера и найдем номера  , для которых выполняется записанное в определении неравенство: , для которых выполняется записанное в определении неравенство:
 ; ;
проведем численный эксперимент, задавая значения малого числа  : :

таким образом, для  можно указать номер можно указать номер  , такой что при , такой что при  верно неравенство верно неравенство  . Это и означает по определению предела, что . Это и означает по определению предела, что  , ч.т.д. , ч.т.д.
 ; ;
отмечая эти числа на координатной оси, видим (рис. 10), что все они с возрастанием номера n попадают в окрестность точки 0, сколь малой бы её ни назначать; отличие от предыдущего примера состоит в том, что здесь числа  приближаются к нулю с обеих сторон. приближаются к нулю с обеих сторон.

Рис. 10
Докажем строго, что  , используя запись определения (2): , используя запись определения (2):
 при при  ; ;
по произвольно зафиксированному числу  находим номер находим номер  , сначала решая записанное в определении неравенство относительно n: , сначала решая записанное в определении неравенство относительно n:
 . .
Например, для конкретных малых значений  получим такие значения получим такие значения  : :

Таким образом, выполнено определение (2) факта  , поэтому , поэтому  , ч.т.д. , ч.т.д.
 , (рис. 11): , (рис. 11):

Рис. 11
По расположению на координатной прямой чисел  предполагаем, что предполагаем, что  . Докажем это строго, используя запись определения (3): . Докажем это строго, используя запись определения (3):
 при при  . .
Решаем неравенство  относительно относительно 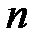 , считая число , считая число  фиксированным, и находим номер фиксированным, и находим номер  , начиная с которого это неравенство выполняется: , начиная с которого это неравенство выполняется:
 , так как , так как  . .
Таким образом, определение (3) выполнено, следовательно,  , ч.т.д. , ч.т.д.


Рис. 12
 не существует, так как нельзя указать такое число а, в любой окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера, (рис. 12). не существует, так как нельзя указать такое число а, в любой окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера, (рис. 12).

 не существует, так как нет такой точки не существует, так как нет такой точки  , для которой бы выполнялось определение предела данной последовательности; это видно по расположению точек , для которой бы выполнялось определение предела данной последовательности; это видно по расположению точек 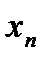 на координатной прямой (рис. 13): не все на координатной прямой (рис. 13): не все  , ,  попадают в попадают в  , хотя члены последовательности с четными номерами очевидно стремятся к 0. , хотя члены последовательности с четными номерами очевидно стремятся к 0.

Рис. 13
 ; ;
для этой последовательности  и значение предела и значение предела  принимается всеми принимается всеми  с четными номерами. с четными номерами.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 элементов некоторого множества
элементов некоторого множества  ℝназывается отображение множества натуральных чисел ℕна это множество
ℝназывается отображение множества натуральных чисел ℕна это множество  ℕ
ℕ  .
.
 значений функции может быть бесконечным счетным или конечным.
значений функции может быть бесконечным счетным или конечным. называются членами последовательности:
называются членами последовательности: - первый член,
- первый член,  - второй член, …,
- второй член, …,  -
-  -й член или общий член последовательности.
-й член или общий член последовательности. просто последовательностью.
просто последовательностью.

 ;
; , т.е.
, т.е.  .
. состоит из одного элемента (то есть все члены последовательности одинаковы),
состоит из одного элемента (то есть все члены последовательности одинаковы),  называется стационарной последовательностью.
называется стационарной последовательностью. , то для неё возможно изображение графиком, например, в декартовой прямоугольной системе координат (рис. 1).
, то для неё возможно изображение графиком, например, в декартовой прямоугольной системе координат (рис. 1).
 для любой последовательности
для любой последовательности  точек на одной координатной оси (рис. 2).
точек на одной координатной оси (рис. 2).
 , она содержит все члены этой последовательности, начиная с некоторого номера
, она содержит все члены этой последовательности, начиная с некоторого номера  .
.
 , или
, или  при
при  , или
, или  .
.
 , то есть
, то есть 
 назначается произвольно; вне выбранной окрестности точки
назначается произвольно; вне выбранной окрестности точки  - окрестность, то нетрудно составить и проиллюстрировать формальное описание конечного предела последовательности (рис.4).
- окрестность, то нетрудно составить и проиллюстрировать формальное описание конечного предела последовательности (рис.4).

 , сколь малым бы оно ни было, можно указать номер
, сколь малым бы оно ни было, можно указать номер  , такой что выполняется неравенство
, такой что выполняется неравенство  для всех номеров
для всех номеров  , то это означает, что члены последовательности
, то это означает, что члены последовательности  , если брать номера
, если брать номера  достаточно большими.
достаточно большими.
 , то иллюстрация к определению
, то иллюстрация к определению  в соответствии с формальной записью (1) имеет вид, приведенный на рис. 5.
в соответствии с формальной записью (1) имеет вид, приведенный на рис. 5.
 может находиться лишь конечное число точек
может находиться лишь конечное число точек  , то получится формальное описание предела, равного
, то получится формальное описание предела, равного  , и его иллюстрация (рис. 6):
, и его иллюстрация (рис. 6):

 , то это означает, что члены последовательности
, то это означает, что члены последовательности  становятся сколь угодно большими положительными, если брать их номера
становятся сколь угодно большими положительными, если брать их номера  достаточно большими.
достаточно большими.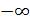
 , то иллюстрация и формальное описание приведены ниже, (рис.7)
, то иллюстрация и формальное описание приведены ниже, (рис.7)

 , то это означает, что члены последовательности
, то это означает, что члены последовательности  становятся сколь угодно большими по модулю, но отрицательными, если брать их номера
становятся сколь угодно большими по модулю, но отрицательными, если брать их номера 
 , то на рис.8 приведена иллюстрация и далее формальное определение:
, то на рис.8 приведена иллюстрация и далее формальное определение:

 , то это означает, что члены последовательности
, то это означает, что члены последовательности  становятся сколь угодно большими по модулю, если брать их номера
становятся сколь угодно большими по модулю, если брать их номера  достаточно большими.
достаточно большими. . При этом полезно наблюдать расположение членов каждой последовательности на координатной оси.
. При этом полезно наблюдать расположение членов каждой последовательности на координатной оси.
 на координатной оси (рис. 9), то нетрудно предположить, что
на координатной оси (рис. 9), то нетрудно предположить, что  , так как в любую окрестность числа 0 попадает в бесконечное множество чисел
, так как в любую окрестность числа 0 попадает в бесконечное множество чисел 
 , пользуясь записью определения (2):
, пользуясь записью определения (2): при
при  .
. и найдем номера
и найдем номера  , для которых выполняется записанное в определении неравенство:
, для которых выполняется записанное в определении неравенство: ;
; :
:
 можно указать номер
можно указать номер  , такой что при
, такой что при  верно неравенство
верно неравенство  . Это и означает по определению предела, что
. Это и означает по определению предела, что  , ч.т.д.
, ч.т.д. ;
; приближаются к нулю с обеих сторон.
приближаются к нулю с обеих сторон.
 , используя запись определения (2):
, используя запись определения (2): при
при  ;
; находим номер
находим номер  , сначала решая записанное в определении неравенство относительно n:
, сначала решая записанное в определении неравенство относительно n: .
. получим такие значения
получим такие значения  :
:
 , поэтому
, поэтому  , ч.т.д.
, ч.т.д. , (рис. 11):
, (рис. 11):
 предполагаем, что
предполагаем, что  . Докажем это строго, используя запись определения (3):
. Докажем это строго, используя запись определения (3): при
при  .
. относительно
относительно 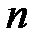 , считая число
, считая число  фиксированным, и находим номер
фиксированным, и находим номер  , начиная с которого это неравенство выполняется:
, начиная с которого это неравенство выполняется: , так как
, так как  .
. , ч.т.д.
, ч.т.д.

 не существует, так как нельзя указать такое число а, в любой окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера, (рис. 12).
не существует, так как нельзя указать такое число а, в любой окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера, (рис. 12).
 не существует, так как нет такой точки
не существует, так как нет такой точки  , для которой бы выполнялось определение предела данной последовательности; это видно по расположению точек
, для которой бы выполнялось определение предела данной последовательности; это видно по расположению точек 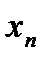 на координатной прямой (рис. 13): не все
на координатной прямой (рис. 13): не все  ,
,  попадают в
попадают в  , хотя члены последовательности с четными номерами очевидно стремятся к 0.
, хотя члены последовательности с четными номерами очевидно стремятся к 0.
 ;
; и значение предела
и значение предела  принимается всеми
принимается всеми  с четными номерами.
с четными номерами.