Теорема Лиувилля.( понятие целой ф-ции. Основная теорема алгебры)
1. Нер-ва Коши для коэф-тов степенного ряда. Обозначим 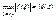 и оценим коэф-т степенного ряда и оценим коэф-т степенного ряда 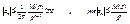 - нер-во Коши. - нер-во Коши.
Опр-е: ф-ция наз-ся целой, если она аналитическая во всей конечной компл пл-ти. Пример. целые ф-ции: многочлен 
2. Т. Лиувилля: если целая ф-ция ограничена по модулю, то она константа. Док-во: степенной ряд .в который разлогается целая ф-ция f(z)= 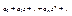 сх-ся во всей пл-ти, т.е; заведомо, в любом круге сх-ся во всей пл-ти, т.е; заведомо, в любом круге  . Пусть по условию . Пусть по условию  . Применим нер-во Коши: . Применим нер-во Коши:  . Учитывая что . Учитывая что  можно выбрать сколь угодно большим, убеждаемся что можно выбрать сколь угодно большим, убеждаемся что 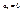 при при  . Теорема доказана. . Теорема доказана.
С помощью этой теоремы может быть установлено, например, алгебраическая замкнутость поля комплексных чисел. Суть ее в основной теореме алгебры.
3. основная теорема алгебры: всякий многочлен  имеет в поле комплексных чисел по крайней мере один корень. Док-во: от противного: пусть нет чисел обращающих имеет в поле комплексных чисел по крайней мере один корень. Док-во: от противного: пусть нет чисел обращающих  в нуль. Тогда в нуль. Тогда  - целая ф-ция, она ограничена по модулю. Действительно, - целая ф-ция, она ограничена по модулю. Действительно,  т.е она ограничена в некоторой окр-ти т-ки т.е она ограничена в некоторой окр-ти т-ки  - во внешности некоторого круга и в нем – тоже (как всякая непрерывная ф-ция) тогда по теореме Лиув. - во внешности некоторого круга и в нем – тоже (как всякая непрерывная ф-ция) тогда по теореме Лиув.  , что противоречит очевидности зависимости ее от z. , что противоречит очевидности зависимости ее от z.
Нули аналитической функции. Изолированность нулей.
Если ряд Тейлора однозначной аналитической ф-и f(z) имеет вид f(z)=ak(z-z0)k+ak+1(z-z0)k+1+...+an(z-z0)n+...(ak≠0), то z0 – нуль кратности k. Если k=1, то k наз-ся простым нулем. Пример: f(z)=1-cos z, z=0. f(0)=1-cos 0=1-1=0. f'(z)=sin z, f'(0)=0, f''(z)=cos z, f''(0)=1≠0 — значит k=2, т.е нуль кратности 2. Очевидно, признак простого нуля f(z0)=0, f'(z0)≠0. Для аналитической ф-ии имеет место след. Теорема: если f(z)≠0 и ф-ия f(z) — аналитическая, то все нули ф-ии f(z) — изолированы. Изолированность нуля означает, что сущ-ет окр-ть нуля, внутри которой нет другого нуля. Будем р!-ь U окр-ть т.z0 и ф-ию f(z)- аналитическую в этой U-окр-ти т.z0, исключая возможно саму т.z0 (рис.1). Возможно 2 случая: 1) сущ-ет такая точка а0, что положив f(z0)=a0, получим аналитическую ф-ию, значит z0 – наз-ся правильной; 2) такое число а0 не сущ-ет, z0-изолированная особая точка. Теорема: т.z0-правильная для аналитической в окр-ти т.z0 ф-ии f(z) (z≠z0)↔сущ-ет U-окр-ть т.z0, в которой |f(z)|-ограничена. Из этой теоремы можно получить признак правильной точки отсутствием ряда  , в соот-ем разложении ф-ии f(z) в виде ряда Лорана (т.е. Отсутствуют коэф-ты с «-» степенями). Если |f(z)|-не ограничена, то z0 – особая точка. Возможны случаи: 1) , в соот-ем разложении ф-ии f(z) в виде ряда Лорана (т.е. Отсутствуют коэф-ты с «-» степенями). Если |f(z)|-не ограничена, то z0 – особая точка. Возможны случаи: 1)  , то т.z0 – наз-ся полюсом. 2) , то т.z0 – наз-ся полюсом. 2)  , тогда т.z0 – наз-ся существенно особой точкой. Пример: , тогда т.z0 – наз-ся существенно особой точкой. Пример: 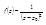 , z0 – полюс кратности 2. Имеет место след. Теорема о взаимосвязи нуля и полюса ф-ии: z0 – полюс f(z) ↔z0 – яв-ся полюсом , z0 – полюс кратности 2. Имеет место след. Теорема о взаимосвязи нуля и полюса ф-ии: z0 – полюс f(z) ↔z0 – яв-ся полюсом  . Т.z0 наз-ся полюсом кратности k для ф-ии f(z), если z0 яв-ся нулем кратности k для ф-ии . Т.z0 наз-ся полюсом кратности k для ф-ии f(z), если z0 яв-ся нулем кратности k для ф-ии  . Учитывая вид степенного ряда для ф-ии f(z), в случаи, когда z0-яв-ся нулем кратности k легко понять, что ряд Лорана будет содержать конечное число членов с «-» степенями, т.е ряд Лорана будет иметь вид: f(z)=a-k(z-z0)-k+...а0+a1(z-z0)+...a-k≠0. Для разложения ф-ии f(z) в окр-ти сущ-но особой точки z0 в ряд Лорана потребуется бесконечно много членов с «-» степенями, поэтому признак сущ-но особой точки — это наличие в ряде Лорана бесконечного числа членов с «-» степенями. . Учитывая вид степенного ряда для ф-ии f(z), в случаи, когда z0-яв-ся нулем кратности k легко понять, что ряд Лорана будет содержать конечное число членов с «-» степенями, т.е ряд Лорана будет иметь вид: f(z)=a-k(z-z0)-k+...а0+a1(z-z0)+...a-k≠0. Для разложения ф-ии f(z) в окр-ти сущ-но особой точки z0 в ряд Лорана потребуется бесконечно много членов с «-» степенями, поэтому признак сущ-но особой точки — это наличие в ряде Лорана бесконечного числа членов с «-» степенями.
Теорема Соходского.
Т. Т-ка   - полюс для f(z) - полюс для f(z)   нуль для нуль для  . док-во: необходимость если . док-во: необходимость если  полюс F(z)то полюс F(z)то  и и 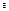 окрестность т-ки окрестность т-ки  , в которой например, , в которой например,  тогда в этой окр-ти тогда в этой окр-ти 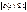 т.е т.е  - правильная т-ка для - правильная т-ка для  причем причем   . Значит . Значит 
Достаточность: Если  - нуль для - нуль для  , то он изолирован: поэтому существ , то он изолирован: поэтому существ  , такое что f(z)- аналетическая, в кольце , такое что f(z)- аналетическая, в кольце  . По скольку . По скольку  - полюс для f(z). Ч.т.д. - полюс для f(z). Ч.т.д.
Опр: т.  - называется полюсом кратности К для f(z) если - называется полюсом кратности К для f(z) если  - нуль кратности К, для - нуль кратности К, для  . .
Учитывая вид степенного ряда, для аналетической функции в окрестности нуля, легко понять, что ряд Лорана построенный в окрестности полюса кратности К для функции содержит конечное число членов с отрицательными стипенями:
 , ,  . Поэтому признак существенно особой точки- наличие бесконечного числа членов с отрицательными степенями в ряде Лорана. Поведение функции в окрестности существенно особой точки заслуживает особого внимания. . Поэтому признак существенно особой точки- наличие бесконечного числа членов с отрицательными степенями в ряде Лорана. Поведение функции в окрестности существенно особой точки заслуживает особого внимания.
Теор Сохоцкого: Если  - существ особая точка для f(z) то, какого бы ни было комплексное число А(не исключая и А= - существ особая точка для f(z) то, какого бы ни было комплексное число А(не исключая и А=  ), существ послед ), существ послед 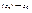 , для которой , для которой  . Док-во: Если А= . Док-во: Если А=  , то теорема очевидна, т.к , то теорема очевидна, т.к 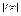 не ограничен во крестности не ограничен во крестности  . Пусть А . Пусть А  . Рассуждаем от противного. Если в любой окрестности . Рассуждаем от противного. Если в любой окрестности  нет точек сколь угодно близких А , то нет точек сколь угодно близких А , то  в некоторой окрестности U ( в некоторой окрестности U (  ) поэтому ) поэтому  ограниченна по модулю в U, т.е ограниченна по модулю в U, т.е  правильная точка для правильная точка для  . Однако . Однако 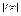 не ограничен в U. Поэтому не ограничен в U. Поэтому  , но тогда , но тогда  - полюс для - полюс для  , т.е и для f(z), что приводит к противоречию с условием теоремы. Ч.т.д. , т.е и для f(z), что приводит к противоречию с условием теоремы. Ч.т.д.
22. Вычет Ф комплексного переменного.Основная теорема о вычетах.
Пусть требуется вычислить интеграл по замкнутому контуру Г от аналитической в обл. D ф-ии f(z),которая может иметь изолированные особые точки z1,…,zn в D.Опишем вокруг zi (i=1…n) окружности  (см. рис). (см. рис).

Тогда  .Разложим f(z) в ряд Лорана в окр-ти т. zi и проинтегрируем по .Разложим f(z) в ряд Лорана в окр-ти т. zi и проинтегрируем по  почленно.Интегралы от всех членов ряда будут равны нулю,кроме того,что относится к члену почленно.Интегралы от всех членов ряда будут равны нулю,кроме того,что относится к члену  и равен и равен 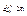 ,поэтому ,поэтому  .Т.о,коэффициент при (z-a)-1 в ряде Лорана,построенном для окрестности изолированной особой т аналитической Ф,играет особую роль при вычислении интегралов.Он наз-ся вычетом f(z) относительно т. а и обозн-ся .Т.о,коэффициент при (z-a)-1 в ряде Лорана,построенном для окрестности изолированной особой т аналитической Ф,играет особую роль при вычислении интегралов.Он наз-ся вычетом f(z) относительно т. а и обозн-ся  (или (или  ) )
Получаемая выше формула носит наз-е основной теоремы о вычетах:
Т:пусть f(z)-аналит-я в обл. G функция,исключая конечное число особых точек.Тогда интеграл от нее по замкнутому контуру Г  G равен умноженной на G равен умноженной на  сумме вычетов относительно особых точек,лежащих внутри Г. сумме вычетов относительно особых точек,лежащих внутри Г.
23.Вычисление вычетов относительно полюса.
1).Вычисление вычетов оказывается сравнительно простым для полюсов.Пусть,например,а-простой полюс.Тогда в его окр-ти ряд Лорана для f(z) имеет вид:  Очевидно поэтому, что Очевидно поэтому, что  . В частности, если . В частности, если  ,где ,где  ,а ,а  имеет простой нуль в т.а имеет простой нуль в т.а  ,тогда ,тогда  . .
Примеры: •Для ф-ии
 разложение в ряд Лорана получается подстановкой вместо разложение в ряд Лорана получается подстановкой вместо  его ряда Тейлора. его ряда Тейлора.
Имеем  , т.е. , т.е.  . .
• 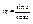 ; ;  имеет в т. имеет в т.  простой нуль, поэтому: простой нуль, поэтому: 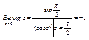
2).Пусть теперь а-полюс кратности к (к>1).Тогда ряд Лорана имеет вид:
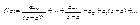 Умножив обе части на Умножив обе части на  и дифференцируя их (к-1), получим: и дифференцируя их (к-1), получим: 
Остается перейти к приделу при   . .
Например, возвращаясь к первому примеру •, замечаем, что в т. z=0 ф-я имеет полюс порядка 3.Поэтому
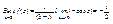 ,т.к. ,т.к. 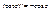 . .
3).Столь же эффективных способов вычисления вычетов в случае существенно особой точки не сущ-ет.Очевидно,что вычет относительно правильной точки равен нулю(по теореме Коши).
4).z0-существенно особая:формул нет,получить разложение в ряд Лорана и по нему найти вычет.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


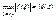 и оценим коэф-т степенного ряда
и оценим коэф-т степенного ряда 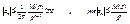 - нер-во Коши.
- нер-во Коши.
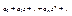 сх-ся во всей пл-ти, т.е; заведомо, в любом круге
сх-ся во всей пл-ти, т.е; заведомо, в любом круге  . Пусть по условию
. Пусть по условию  . Применим нер-во Коши:
. Применим нер-во Коши:  . Учитывая что
. Учитывая что  можно выбрать сколь угодно большим, убеждаемся что
можно выбрать сколь угодно большим, убеждаемся что 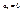 при
при  . Теорема доказана.
. Теорема доказана. имеет в поле комплексных чисел по крайней мере один корень. Док-во: от противного: пусть нет чисел обращающих
имеет в поле комплексных чисел по крайней мере один корень. Док-во: от противного: пусть нет чисел обращающих  в нуль. Тогда
в нуль. Тогда  - целая ф-ция, она ограничена по модулю. Действительно,
- целая ф-ция, она ограничена по модулю. Действительно,  т.е она ограничена в некоторой окр-ти т-ки
т.е она ограничена в некоторой окр-ти т-ки  - во внешности некоторого круга и в нем – тоже (как всякая непрерывная ф-ция) тогда по теореме Лиув.
- во внешности некоторого круга и в нем – тоже (как всякая непрерывная ф-ция) тогда по теореме Лиув.  , что противоречит очевидности зависимости ее от z.
, что противоречит очевидности зависимости ее от z. , в соот-ем разложении ф-ии f(z) в виде ряда Лорана (т.е. Отсутствуют коэф-ты с «-» степенями). Если |f(z)|-не ограничена, то z0 – особая точка. Возможны случаи: 1)
, в соот-ем разложении ф-ии f(z) в виде ряда Лорана (т.е. Отсутствуют коэф-ты с «-» степенями). Если |f(z)|-не ограничена, то z0 – особая точка. Возможны случаи: 1)  , то т.z0 – наз-ся полюсом. 2)
, то т.z0 – наз-ся полюсом. 2)  , тогда т.z0 – наз-ся существенно особой точкой. Пример:
, тогда т.z0 – наз-ся существенно особой точкой. Пример: 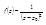 , z0 – полюс кратности 2. Имеет место след. Теорема о взаимосвязи нуля и полюса ф-ии: z0 – полюс f(z) ↔z0 – яв-ся полюсом
, z0 – полюс кратности 2. Имеет место след. Теорема о взаимосвязи нуля и полюса ф-ии: z0 – полюс f(z) ↔z0 – яв-ся полюсом  . Т.z0 наз-ся полюсом кратности k для ф-ии f(z), если z0 яв-ся нулем кратности k для ф-ии
. Т.z0 наз-ся полюсом кратности k для ф-ии f(z), если z0 яв-ся нулем кратности k для ф-ии  . Учитывая вид степенного ряда для ф-ии f(z), в случаи, когда z0-яв-ся нулем кратности k легко понять, что ряд Лорана будет содержать конечное число членов с «-» степенями, т.е ряд Лорана будет иметь вид: f(z)=a-k(z-z0)-k+...а0+a1(z-z0)+...a-k≠0. Для разложения ф-ии f(z) в окр-ти сущ-но особой точки z0 в ряд Лорана потребуется бесконечно много членов с «-» степенями, поэтому признак сущ-но особой точки — это наличие в ряде Лорана бесконечного числа членов с «-» степенями.
. Учитывая вид степенного ряда для ф-ии f(z), в случаи, когда z0-яв-ся нулем кратности k легко понять, что ряд Лорана будет содержать конечное число членов с «-» степенями, т.е ряд Лорана будет иметь вид: f(z)=a-k(z-z0)-k+...а0+a1(z-z0)+...a-k≠0. Для разложения ф-ии f(z) в окр-ти сущ-но особой точки z0 в ряд Лорана потребуется бесконечно много членов с «-» степенями, поэтому признак сущ-но особой точки — это наличие в ряде Лорана бесконечного числа членов с «-» степенями.
 - полюс для f(z)
- полюс для f(z) 
 . док-во: необходимость если
. док-во: необходимость если  и
и 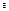 окрестность т-ки
окрестность т-ки  тогда в этой окр-ти
тогда в этой окр-ти 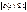 т.е
т.е  причем
причем  . Значит
. Значит 
 - нуль для
- нуль для  , то он изолирован: поэтому существ
, то он изолирован: поэтому существ  . По скольку
. По скольку  - полюс для f(z). Ч.т.д.
- полюс для f(z). Ч.т.д. .
. ,
,  . Поэтому признак существенно особой точки- наличие бесконечного числа членов с отрицательными степенями в ряде Лорана. Поведение функции в окрестности существенно особой точки заслуживает особого внимания.
. Поэтому признак существенно особой точки- наличие бесконечного числа членов с отрицательными степенями в ряде Лорана. Поведение функции в окрестности существенно особой точки заслуживает особого внимания.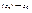 , для которой
, для которой  . Док-во: Если А=
. Док-во: Если А= 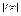 не ограничен во крестности
не ограничен во крестности  . Рассуждаем от противного. Если в любой окрестности
. Рассуждаем от противного. Если в любой окрестности  в некоторой окрестности U (
в некоторой окрестности U (  ) поэтому
) поэтому  ограниченна по модулю в U, т.е
ограниченна по модулю в U, т.е  . Однако
. Однако  , но тогда
, но тогда  , т.е и для f(z), что приводит к противоречию с условием теоремы. Ч.т.д.
, т.е и для f(z), что приводит к противоречию с условием теоремы. Ч.т.д. (см. рис).
(см. рис).
 .Разложим f(z) в ряд Лорана в окр-ти т. zi и проинтегрируем по
.Разложим f(z) в ряд Лорана в окр-ти т. zi и проинтегрируем по  и равен
и равен 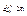 ,поэтому
,поэтому  .Т.о,коэффициент при (z-a)-1 в ряде Лорана,построенном для окрестности изолированной особой т аналитической Ф,играет особую роль при вычислении интегралов.Он наз-ся вычетом f(z) относительно т. а и обозн-ся
.Т.о,коэффициент при (z-a)-1 в ряде Лорана,построенном для окрестности изолированной особой т аналитической Ф,играет особую роль при вычислении интегралов.Он наз-ся вычетом f(z) относительно т. а и обозн-ся  (или
(или  )
) G равен умноженной на
G равен умноженной на  сумме вычетов относительно особых точек,лежащих внутри Г.
сумме вычетов относительно особых точек,лежащих внутри Г. Очевидно поэтому, что
Очевидно поэтому, что  . В частности, если
. В частности, если  ,где
,где  ,а
,а  имеет простой нуль в т.а
имеет простой нуль в т.а  ,тогда
,тогда  .
. разложение в ряд Лорана получается подстановкой вместо
разложение в ряд Лорана получается подстановкой вместо  его ряда Тейлора.
его ряда Тейлора. , т.е.
, т.е.  .
.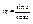 ;
;  простой нуль, поэтому:
простой нуль, поэтому: 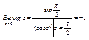
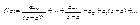 Умножив обе части на
Умножив обе части на  и дифференцируя их (к-1), получим:
и дифференцируя их (к-1), получим: 

 .
.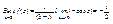 ,т.к.
,т.к. 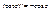 .
.