
|
|
Погрешности косвенных измерений12 При косвенных измерениях искомую величину 1). Искомая величина - функция одной переменной. Пусть При измерении величины x будет допущена погрешность, которую вычисляют по формулам (3) и (4). За счет этого полученное значение а) абсолютная погрешность функции равна абсолютной погрешности аргумента, умноженной на производную этой функции по этому аргументу:
б) относительная погрешность функции равна абсолютной погрешности аргумента, умноженной на производную от логарифма этой функции по этому аргументу: Заметим, что обе формулы (5) и (6) одновременно не используют, так как, если найдена одна из погрешностей (абсолютная или относительная), можно найти другую из соотношения: 2). Если искомая величина является функцией нескольких переменных а) Общую абсолютную погрешность функции определяют через "частные" погрешности следующим образом: б) Общую относительную погрешность функции аналогичным образом выражают через "частные" относительные погрешности. Например, Формула (7) удобнее, если функция представляет собой сумму, а (8) - если произведение. 3). В некоторых случаях косвенных измерений вычисление случайных погрешностей можно свести к уже рассмотренным для прямых измерений способам. Это бывает, если косвенные измерения произведены несколько раз, но условия измерения невоспроизводимы. Тогда данные прямых измерений нельзя усреднять. Например, определяя скорости пули, мы не можем повторить измерение с одной и той же пулей, а измеряем скорость нескольких пуль. В таких случаях значение функции (скорость пули) вычисляют для каждого отдельного измерения и получают набор значений функции ПРИМЕР 2. Пусть искомая величина представляет собой плотность шарика, которая выражена через его массу и объем:
Здесь плотность r есть функция массы m и диаметра d, которые измерены непосредственно. Так как функция представляет собой произведение, то удобнее найти сначала относительную погрешность er по формуле (8). Для этого нужно прологарифмировать функцию r=r(m,d), а затем найти частные производные по m и d:
Частные погрешности Общая относительная погрешность плотности
m и d будут известны из прямых измерений; абсолютные погрешности ПРИМЕР 3. Для определения коэффициента вязкости жидкости наблюдают падение в ней металлического шарика и измеряют время прохождения им определенного пути. Наблюдают последовательно падение нескольких разных шариков. Коэффициент вязкости определяют по формуле:
Величины d, l и t измеряют непосредственно, причем погрешности приборов очень малы. В этом случае нужно вычислить

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 рассматривают как функцию одной или нескольких других величин x, y, z, измеряемых непосредственно при проведении эксперимента. Рассмотрим следующие случаи.
рассматривают как функцию одной или нескольких других величин x, y, z, измеряемых непосредственно при проведении эксперимента. Рассмотрим следующие случаи. .
. . Для оценки погрешности функции удобно пользоваться формулами дифференциального исчисления, из которых следует:
. Для оценки погрешности функции удобно пользоваться формулами дифференциального исчисления, из которых следует: (5)
(5)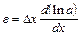 (6)
(6) .
. , обусловленных каждой переменной в отдельности. Каждую из "частных" погрешностей находят по формулам (5) или (6), причем при нахождении
, обусловленных каждой переменной в отдельности. Каждую из "частных" погрешностей находят по формулам (5) или (6), причем при нахождении  берут частную производную по x; остальные переменные y и z при этом считают постоянными коэффициентами. Аналогично - для
берут частную производную по x; остальные переменные y и z при этом считают постоянными коэффициентами. Аналогично - для  . Все частные производные вычисляют при средних значениях
. Все частные производные вычисляют при средних значениях  . Погрешности
. Погрешности  (если это случайные погрешности) должны быть вычислены при одном и том же значении коэффициента надежности a.
(если это случайные погрешности) должны быть вычислены при одном и том же значении коэффициента надежности a. (7)
(7) , тогда
, тогда  (8)
(8) , среднюю квадратичную погрешность, коэффициент Стьюдента t и
, среднюю квадратичную погрешность, коэффициент Стьюдента t и 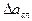 . Этим способом удобно пользоваться, если погрешности приборов значительно меньше случайных погрешностей и ими можно пренебречь. В противном случае нужно найти полную погрешность
. Этим способом удобно пользоваться, если погрешности приборов значительно меньше случайных погрешностей и ими можно пренебречь. В противном случае нужно найти полную погрешность  по формулам (7) или (8).
по формулам (7) или (8).

 .
.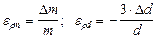

 и
и  определяют по формулам (3) и (4). Относительные погрешности
определяют по формулам (3) и (4). Относительные погрешности  и
и  можно представить в процентах, тогда
можно представить в процентах, тогда  тоже получим в процентах. Абсолютная погрешность плотности будет
тоже получим в процентах. Абсолютная погрешность плотности будет  , где
, где 
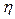 i для каждого шарика отдельно. Получим несколько значений
i для каждого шарика отдельно. Получим несколько значений  , среднюю квадратичную погрешность S, коэффициент Стьюдента t и случайную погрешность
, среднюю квадратичную погрешность S, коэффициент Стьюдента t и случайную погрешность  и далее, как в примере 1, относительную погрешность и окончательный результат:
и далее, как в примере 1, относительную погрешность и окончательный результат: при eh =..., α =…..
при eh =..., α =…..