
|
|
Путь минимальной суммарной длины во взвешенном графе с произвольными весами для всех пар вершин (алгоритм Флойда)
Следует заметить, что если в графе существует контур отрицательной сумарной длины, то вес любого пути, проходящего через вершину из этого контура, можно сделать сколь угодно малой, "прокрутившись" в контуре необходимое количество раз. Поэтому поставленная задача разрешима не всегда. В случае, описанном выше, алгоритм Флойда прекращает свою работу. Останавливаясь подробнее, надо заметить, что если граф неориентированный (W[i,j]- симметрична), то ребро с отрицательным весом является как раз таким контуром (туда-сюда можно бегать пока не сделаем вес достаточно малым) Алгоритм Флойда предполагает последовательное преобразование матрицы весов W. В конечном итоге получаем матрицу, элементы d[i,j] которой представляют из себя вес минимального пути соединяющего i и j вершины. Рассмотрим преобразования матрицы весов: Преобразование проделывается для m=1..n, где n - мощность множества вершин графа. Если на некотором шаге получим отрицательное dm[i,m]+dm[m,i] для какого-нибудь i, то в графе существует контур отрицательного веса, проходящий через вершину i, и задача не разрешима. На выходе получаем матрицу D минимальных весов и матрицу P, при помощи которой можно востановить путь минимального веса следующим образом: значение p[i,j] будет равно номеру предпоследней вершины в пути между i и j (либо p[i,j]=i, если путь не существует). Переменная s на выходе равна 1, если алгоритм отработал полностью, и нулю, если в ходе работы алгоритма найден контур отрицательного веса.
6.4.4. Нахождение K путей минимальной суммарной длины во взвешенном графе с неотрицательными весами (алгоритм Йена)
Работа алгоритма начинается с нахождения кратчайшего пути, для этого будем использовать уже описанный алгоритм Дейкстры. Второй путь щем, перебирая кратчайшие отклонения от первого, третий кратчайшие отклонения от второго и т.д. Более точное пошаговое описание: 1. Найти минимальный путь P1=(v11,...,v1L[1]). Положить k = 2. Включить P1 в результирующий список. 2. Положить MinW равным бесконечности. Найти отклонение минимального веса от (k–1)-го кратчайшего пути Pk-1 для всех i=1,2,...,L[k-1], выполняя для каждого i шаги с 3-го по 6-й. 3. Проверить, совпадает ли подпуть, образованный первыми i вершинами пути Pk-1, с подпутем, образованным первыми i вершинами любого из путей j=1,2,...,k–1). Если да, положить W[vk-1i,vji+1] равным бесконечности, в противном случае ничего не изменять (чтобы в дальнейшем исключить получение в результате одних и тех же путей). 5. Построить путь, объединяя корень и найденное кратчайшее ответвление; если его вес меньше MinW, то запомнить его. 6. Восстановить исходную матрицу весов W и возвратиться к шагу 3. Алгоритм использует массив p для результирующего списка путей, и массив l для хранения соответствующих длин, при этом, если начиная с некоторого i элементы l[i] равны -1, значит существует только i-1 кратчайших путей без петель. Классы и объекты По мере прогресса в области вычислительной математики акцент в программировании смещается в какую-либо сторону. Первой была идея процедурного структурирования программ, затем – организация данных. В настоящее время акцент делается на объектно-ориентированное программирование(ООП). Его руководящая идея заключается в стремлении связать данные с обрабатывающими эти данные процедурами в единое целое – объект. Класс (class) и объект (object) – два общепринятых термина. Однако, поскольку имеется несколько различных трактовок этих понятий, давайте сразу договоримся о том, как их будем понимать мы. Классом называется определенный пользователем тип данных, который включает в себя состояние (представление класса) и некие операции (поведение класса). Класс имеет некоторое количество внутренних данных и несколько методов, существующих в форме процедур и функций, и обычно описывает общее поведение и характеристики набора аналогичных друг другу объектов. Объект есть экземпляр класса или, другими словами, переменная, тип которой является классом. Объекты в отличие от классов реальны в том смысле, что во время выполнения программы они хранятся в памяти. Соотношения между объектом и классом аналогичны соотношениям между переменной и типом. К сожалению, в некоторых языках и средах эта разница не столь ясна. Дополнительную сложность создает также то обстоятельство, что ранние версии компилятора Borland Pascal использовали ключевое слово object для определения классов. По этой причине программисты на Pascal со стажем предпочитают использовать для обозначения типа термин “объект” вместо термина “класс”, а для обозначения реальных объектов - термин “экземпляр объекта” (object instance). Чтобы определить в Object Pascal новый класс данных, имеющий свои поля данных и методы, используется следующий синтаксис: Type Tdate=class Month, Day, Year: Integer; procedure SetValue (m,d,y,: integer); function LeapYear: Boolean: end; Методы класса должны быть реализованы в коде: чтобы подчеркнуть, что они являются частью класса Tdate. В Delphi принимается соглашение об использование трефикса Т перед именем каждого определяемого класса. Это лишь соглашение, поскольку компилятор воспринимает символ Т точно так же, как и все остальные буквы, но оно настолько распространено, что следование ему сделает ваш код значительно понятнее. Другое соглашение заключается в том, чтобы использовать двух- или трехбуквенный префикс для указания разработчика класса ( фирмы или конкретного человека). Это соглашение является общепринятым для компонентов. Рекурсия Рекурсивным называется объект, частично состоящий или определяемый с помощью самого себя. Рекурсивные определения представляют собой мощный аппарат в математике. Например: 1. Натуральные числа: а) 1 есть натуральное число, б) число, следующее за натуральным, есть натуральное число. 2. Деревья: а) 0 есть дерево ("пустое дерево"), б) если А1 и А2 - деревья, то построение, содержащее вершину с двумя ниже расположенными деревьями, опять дерево. 3. Функция n! "факториал" (для неотрицательных целых чисел): а) 0!=1, б) n>0: n!=n·(n-1)! Мощность рекурсивного определения заключается в том, что оно позволяет с помощью конечного высказывания определить бесконечное множество объектов. Аналогично, с помощью конечной рекурсивной программы можно описать бесконечное вычисление, причем программа не будет содержать явных повторений. В общем виде рекурсивную программу Р можно выразить как некоторую композицию Р из множества операторов С (не содержащих Р) и самой Р: Р=Р[С,Р]. Для выражения рекурсивных программ удобнее пользоваться процедурами или функциями. Если некоторая процедура Р содержит явную ссылку на саму себя, то ее называют прямо рекурсивной, если же Р ссылается на другую процедуру В, содержащую ссылку на Р, то Р называют косвенно рекурсивной. Как правило, с процедурой связывают множество локальных переменных, которые определены только в этой процедуре. При каждой рекурсивной активации процедуры порождается новое множество локальных, связанных переменных. Хотя они имеют те же самые имена, что и соответствующие элементы локального множества предыдущего "поколения" этой процедуры, их значения отличны от последних, а любые конфликты по именам разрешаются с помощью правил, определяющих область действия идентификаторов: идентификатор всегда относится к самому последнему порожденному множеству переменных. Рекурсивные процедуры могут приводить к не заканчивающимся вычислениям. Очевидно основное требование, чтобы рекурсивное обращение к Р управлялось некоторым условием Х, которое в какой-то момент становится ложным. Р== if X then P[C,P] Основной способ доказательства конечности некоторого повторяющегося процесса: 1. Определяется функция f(x), такая, что из f(x) 2. Доказывается, что при каждом прохождении цикла f(x) уменьшается. Аналогично доказывается и окончание рекурсии - показывается, что Р уменьшает f(x), такую, что из f(x) В практических приложениях важно убедиться, что максимальная глубина рекурсий не только конечна, но и достаточно мала. Дело в том, что каждая рекурсивная активация процедуры Р требует памяти для размещения ее переменных. Кроме этих переменных нужно еще сохранять текущее "состояние вычислений", чтобы можно было вернуться в него по окончании новой активации Р. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
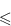 0 следует истинность условия окончания цикла.
0 следует истинность условия окончания цикла.