
|
|
Приложение 2. Знакомство с пакетами расширения системы MATLABДля решения специализированных задач разработаны пакеты расширений системы MATLAB с дополнительными функциями. Такие пакеты называются ToolBoxes. При установке системы MATLAB пользователь может выборочно загрузить нужные ему пакеты. Например, пакет Symbolic Math ToolBoxдобавляет к системе возможность символьных вычислений (Глава 7), пакет Partial Differentional Equation ToolBox (PDE ToolBox) создан для исследования задач математической физики (см. приложение 1). Если пакет расширения установлен, он становится компонентой расширенной системы MATLAB, а раздел с одноименным оглавлением включается в список вкладки Contents панели Help Navigator (рис. П.9). Команда ver, выполняемая из командной строки, выводит название, номер версии и дату создания всех установленных ToolBox. Перечень пакетов расширений версии MATLAB 6.5 содежит десятки наименований. По большинству таких расширений опубликованы отдельные книги, а объем документации по ним составляет сотни мегабайт. В MATLAB 7 расширены возможности многих ToolBox по сравнению с версией 6.5. Ниже дан краткий обзор основных возможностей некоторых ToolBox.
Simulink (моделирование нелинейных систем)
Система имитационного моделирования Simulink – самое популярное расширение MATLAB. Кнопка его вызова вынесена на панель инструментов главного окна рабочей среды (перед кнопкой ?), т.к. MATLAB содержит Simulink в своем составе. Пакет Simulink предназначен для математического моделирования линейных и нелинейных динамических систем и устройств, представленных своей функциональной блок - схемой, именуемой моделью. Simulink имеет обширную библиотеку блочных компонентов, редактор блок - схем и по существу является средством визуального программирования. С помощью мыши пользователь переносит нужные компоненты на рабочий стол системы и соединяет линиями входы и выходы блоков. Таким образом создается блок - схема системы или устройства. В состав моделей могут включаться источники сигналов различного вида, преобразователи с разнообразными формами передаточных характеристик, интегрирующие и дифференцирующие блоки, виртуальные регистрирующие приборы, графические средства анимации. Двойной щелчок мышью на блоке модели выводит окно со списком его параметров, которые пользователь может менять. Запуск имитации обеспечивает математическое моделирование построенной модели с наглядным визуальным представлением результатов. На всех этапах работы, особенно при подготовке моделей схем, пользователь практически не имеет дела с обычным программированием. Программа автоматически генерируется в процессе ввода выбранных блоков компонентов, их соединений и задания параметров компонентов. Некоторые продукты семейства Simulink: SimMechanics – моделирование физических систем в среде Simulink; SimPowerSystems – моделирование электротехнических устройств и систем в Simulink; Communications Blockset – набор блоков для разработки и моделирования физического уровня телекоммуникационных систем и их компонентов в Simulink; Signal Processing Blockset – набор блоков для моделирования в Simulink поточных данных и многоскоростных систем, применяемых в телекоммуникациях, цифровых системах управления, радио- и гидролокации и других прикладных областях, требующих больших объемов вычислений.
Optimization ToolBox (решение оптимизационных задач)
Пакет Optimization ToolBox предназначен для решения основных линейных и нелинейных задач оптимизации, причем для задач большой размерности предусмотрены эффективные специальные методы. Класс задач, поддеживаемый данным ToolBox, включает: □ решение нелинейных уравнений; □ линейное и квадратичное программирование; □ безусловная оптимизация нелинейных функций; □ условная минимизация нелинейных функций при наличии нелинейных ограничений; □ подбор параметров; □ минимаксные задачи.
Statistics ToolBox (статистические вычисления)
Функции и приложения Statistics ToolBox расширяют возможности системы в области реализации статистических вычислений и статистической обработки данных. Класс задач, поддеживаемый данным ToolBox, включает: □ исследование линейных моделей; □ распределения вероятностей; □ параметричесое оценивание; □ проверка гипотез; □ множественная регрессия; □ планирование эксперимента; □ статистические графики; □ графический интерфейс пользователя.
Signal Processing ToolBox (цифровая обработка сигналов)
Основные возможности пакета: □ генерация, импорт и экспорт сигналов; □ проектирование, анализ и реализация цифровых и аналоговых фильтров; □ спектральный анализ и статистическая обработка сигналов; □ быстрое преобразование Фурье, дискретное косинусное и другие преобразования, применяемые для анализа, кодирования и фильтрации; □ моделирование линейных систем. В состав пакета входит несколько приложений с графическим интерфейсом, предназначенных для облегчения доступа к функциям ToolBox.
Control System ToolBox (исследование систем управления)
Пакет Control System ToolBox содержит специализированные инструменты для разработки и анализа контроллеров систем управления и динамических систем с обратной связью. В пакете реализованы: □ полный набор средств для анализа систем; □ временные характеристики: передаточная и переходная функции, реакция на призвольное воздействие; □ частотные характеристики: диаграммы Боде, Николса, Найквиста и др.; □ характеристики моделей: управляемость, наблюдаемость, понижение порядка моделей; □ поддежка систем с запаздыванием.
Communications ToolBox (исследование телекоммуникационных систем):
□ генерация случайных сигналов; □ анализ ошибок, включая визуальные диаграммы и графики в трехмерном пространстве; □ кодирование сигнала, поступающего с источника сообщений, включая квантование, дифференциальную импульсно - кодовую модуляцию и компандер; □ помехоустойчивое кодирование, включая свертку и линейно - блочное кодирование; □ аналоговая и цифровая модуляция / демодуляция; □ фильтрация данных с использованием специальных фильтров; □ вычисления в полях Галуа.
Image Processing Toolbox
Пакет предоставляет пользователю широкие возможности в области цифровой обработки и анализа изображений. Основные направления в этой области, которые реализованы в пакете, заключаются в следующем: □ фильтрация с использованием ряда алгоритмов изображений, позволяющая улучшить качество изображения и уменьшить негативное влияние шумов; □ обработка выделенных участков изображения с целью коррекции или улучшения качества восприятия; □ анализ свойств изображений и получение их статистических характеристик; □ цветоаые преобразования, в том числе, связанные с изменением палитры; □ импорт, обработка и экспорт изображений, представленных в файлах с различными форматами. Приложение 3. Задания для самостоятельной работы За номером задания в скобках указан раздел, после которого выполняется задание.
Задание 1 (1.8). Ввести и вычислить арифметическое выражение
Требуется занести в выражение значения переменных x = -1,5∙10-2, y = 2,2π и вычислить его. Проконтролировать с помощью команды pretty ввод выражения. Отобразить результат вычисления в различных форматах. Варианты 1. F = th 2. Z = arctg 3. W = sh 4. T = sin 5. R = cth 6. C = ctg 7. H = 8. U = 9. A = 10. V = cth 11. S = 12. Q = 13. B = arcctg 14. P = sin 15. G = arcsh Задание 2 (1.10). Вычислить матричное выражение
Ввести матрицы А = , B = , C = и найти значение заданного выражения. Если результат не целочисленный, отобразить его в формате rat. Изучить информацию о переменных при помощи команды whos. Открыть окно для просмотра переменных рабочей среды Workspace. Заменить с использованием редактора Array Editor матрицы A, B, C на новые
А = , B = , C = , и повторить вычисления.
Варианты
1. (A3+CB)(A2+2CB)T 2. A4+3A2−ACB 3. BAC−5CTBT 4. 2BA-1C−BAC+3BC 5. -2CTAC−BBT 6. (BCB−2CT)A2 7. (ABT−C)(C+ABT)T 8. (ABTB)3BTCTA 9. CT(BTB+CCT)C 10. AAT−(CB)2+3(CB)-2 11. (BTB−3AT)A-2 12. (CBATC−C)(C+CBATC)T 13. (2CTAC−BBT)CT +B 14. 2C(BBT+CTC)CT+CB−A3 15. CB−(AAT)2+3CBA Задание 3 (1.11). Решить систему линейных алгебраических уравнений
Дана система линейных алгебраических уравнений Ах = в. Вычислить определитель │А│. Если │А│ ≠ 0, решить систему с помощью оператора обратного деления < \ >.Проверить решение подстановкой. Вычислить обратную матрицу А-1 и решить систему с помощью с помощью обратной матрицы. Если полученное решение приближенное, повторить вычисления в формате rat.
Варианты 1.
4.
7.
10. 12.
14.
Задание 4 (2.2). Создание векторов и применение к ним математических операций и команд обработки данных
Для заданных векторов a и b длины n: 1. вычислить их сумму, разность и скалярное произведение; 2. образовать вектор с =[a1,a2,…,an,b1,b2,…,bn], определить его максимальный и минимальный элементы и поменять их местами; 3. упорядочить вектор c по возрастанию и убыванию; 4. переставить элементы вектора c в обратном порядке и записать результат в новый вектор (с помощью rot90); 5. найти векторное произведение u=[a2,a5,a6] и v=[b1,b3,b5] (с помощью cross).
Варианты 1. a = [1.2 2.5 6.0 -4.3 1.2 -2.7 2.4 2.2]; b = [1.2 5.0 7.0 5.4 2.6 -2.7 4.6 0.3]. 2.a =[-1.3 -2.8 -1.0 0.7 4.0 8.5 4.3 -4.0];b =[-2.9 -5.4 7.1 -2.1 6.8 5.2 0.3 1.6]. 3. a = [3.2 -7.5 -2.3 -4.3 -1.7 1.2 -0.6 1.8]; b = [4.6 -5.7 -1.2 2.4 0.4 -2.0 -7.1 -5.2]. 4. a = [5.1 2.8 -0.1 3.6 7.4 -2.8 0.3 1.2]; b = [3.5 1.4 4.3 -3.7 5.0 3.7 8.1 8.0]. 5. a = [4.2 -1.1 -2.5 -4.9 0.9 -1.7 1.7 0.8]; b = [-0.5 1.0 1.2 7.5 5.0 -3.0 -6.2 1.0]. 6. a = [3.5 6.8 -7.1 6.8 -5.0 -2.3 -4.4 -0.2]; b = [5.5 1.5 5.7 -4.6 -2.3 -5.3 5.5 2.3]. 7. a = [2.2 4.2 -0.8 -0.7 -2.2 1.7 3.3 -6.1]; b = [2.5 3.7 1.0 -4.3 -0.0 -1.8 -1.5 2.4]. 8. a = [0.6 5.0 -7.7 8.3 3.8 1.9 1.1 2.7]; b = [5.0 2.2 1.2 -2.9 1.9 -6.5 -6.2 -8.1]. 9. a = [2.9 0.4 -1.8 2.2 -3.8 -4.7 4.0 -2.1]; b = [7.7 4.8 -1.2 2.8 -2.2 7.8 0.0 -0.1]. 10. a = [1.9 -1.7 3.2 -3.8 7.3 6.0 -0.2 8.6]; b = [-0.2 1.4 3.9 -2.2 1.6 3.8 -3.2 0.4]. 11. a = [0.5 3.7 6.0 -4.3 1.2 -2.7 2.4 2.2]; b = [3.6 7.0 7.0 5.4 2.6 -2.7 -6.4 0.3]. 12.a =[-4.8 -1.3 -1.0 0.7 4.0 5.8 4.3 -8.0];b =[-1.1 -1.9 7.1 -2.1 6.8 2.8 0.3 1.6]. 13. a = [1.0 -3.9 -2.3 -3.3 -1.7 2.2 -0.6 1.8]; b = [2.7 -2.7 -2.2 4.4 0.4 -6.0 -3.4 -5.2]. 14. a = [-2.4 3.3 -0.1 3.6 7.4 -2.8 0.3 2.2]; b = [6.3 0.6 4.3 -3.7 -7.0 3.7 3.7 8.0]. 15. a = [8.4 -5.9 -6.5 -0.9 6.9 -1.7 1.7 0.8]; b = [-0.0 2.0 -1.5 7.5 -4.0 -3.0 -6.2 0.0]. Задание 5 (2.3, 2.4). Создать матрицу и применить команды обработки данных и поэлементных операций для нахождения заданных величин
Сконструировать при помощи команд создания специльных матриц, индексации двоеточием и, возможно, поворота, транспонирования или вычеркивания следующие матрицы и применить команды обработки данных и поэлементные операции для нахождения заданных величин.
Варианты
Задание 6 (2.5). Найти собственные числа и векторы матрицы, ее характеристический полином, ранг и определитель
Для матрицы A из соответствующего варианта Задания 5 найти собственные числа и векторы матрицы A, ее характеристический полином, ранг и определитель.
Задание 7 (3.2, гл.5). Написать файл-функцию для решения поставленной задачи
Варианты 1. Переставить последнюю строку квадратной матрицы с ее побочной диагональю. 2. По заданному вектору определить номер его элемента с наименьшим отклонением от среднего арифметического всех элементов вектора. 3. Суммировать все элементы заданной матрицы, лежащие выше главной диагонали. 4. Возвратить произведение всех элементов вектора с индексами, кратными трем. 5. Переставить первый столбец 6. Вычислить произведение максимального и минимального значений среди диагональных элементов заданной матрицы. 7. Возвратить сумму всех элементов вектора с нечетными индексами. 8. Вычислить минимальное значение среди диагональных элементов заданной матрицы. 9. Суммировать все элементы заданной матрицы без главной диагонали. 10. Заменить максимальный элемент вектора средним значением всех его элементов. 11. Заменить элемент матрицы с индексами 1,1 суммой всех элементов матрицы. 12. Построить многоугольник (замкнутый) по заданным векторам x и y с координатами вершин. 13. Для заданной квадратной матрицы найти скалярное произведение строки, в которой находится наибольший элемент матрицы, на столбец с наименьшим элементом. 14. Отобразить элементы заданного вектора синими маркерами, а максимальный элемент – красным и возвращает значение и номер максимального элемента. 15. Перевести время в секундах в часы, минуты и секунды.
Задание 8 (4.3). Написать файл-функцию для вычисления Кусочно-заданной функции
Варианты 1. f(x)= 4. f(x)= 6. f(x)= 9. f(x)= 11. f(x)= 13. f(x)= 15. f(x)= Задание 9 (4.5, гл.5). Написать файл-функцию для решения поставленной задачи
Варианты 1.Заменить отрицательные элементы вектора суммой суммой модулей всех его отрицательных элементов. 2. Вычислить произведение элементов вектора, не превосходящих среднее арифметическое значение модулей его элементов. 3.Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (таковы, например, числа 41 и 43). Сформировать матрицу, строками которой являтся все пары «близнецов» из отрезка [n;2n], где n – заданное целое число, большее 2. 4 Подсчитать число нулей и единиц в заданной матрице. 5. Определить количество положительных элементов вектора, расположенных между его первыми максимальным и минимальным элементами. 6. Число называется «совершенным», если оно равно сумме своих делителей, включая 1, за исключением его самого (таково, например, число 6: 6=1+2+3). Сформировать маccив всех «совершенных» чисел, не превосходящих заданного натурального числа. 7. Просуммировать положительные элементы матрицы, лежащие выше главной диагонали. 8. Заменить положительные элементы вектора суммой всех его отрицательных элементов. 9. Заполнить квадратную матрицу A, каждый элемент которой aij определяется следующим образом:
10. Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Сформировать матрицу, строками которой являтся все пары «дружественных» чисел, не превосходящих заданного натурального числа. 11. Вычислить сумму:
12. Для матрицы A = (aij) размера n на m найти значение выражения:
13. По заданному x ≥ 0 найти максимальное значение n, для которого следующая сумма не превосходит 200:
14. Вычислить сумму
с заданной точностью ε. Суммировать следует пока модуль отношения текущего слагаемого к уже накопленной части суммы превосходит ε. Сравнить результат с точным значением, построив графики ex и s(x) для 0 ≤ x≤ 0,5. 15. Заданы окружности, координаты их центров содержатся в массивах x и y, а радиусы в массиве r. Известны координаты некоторой точки. Требуется вывести график, на котором маркером отмечено положение точки, синим цветом изображены те окружности, внутри которых лежит точка, а остальные окружности нарисованы красным цветом. Задание 10 (5.1.1). Создать файл-функцию для построения графиков С помощью plot и fplot Написать файл-функции и построить графики на заданном отрезке при помощи plot (с шагом 0.05) и fplot для следующих функций:
Варианты
1. f(x) = , 0≤ x ≤1 2. f(x) = , 0≤ x ≤1 3. f(x) = , 0≤ x ≤1 4. f(x) = sin2πx , 0≤ x ≤1 5. f(x) = sin , 0≤ x ≤1 6. f(x) = , 0≤ x ≤1 7. f(x) = e3sin5πx+ e3cos5πx, 0≤ x ≤1 8. f(x) = sin , 0,05≤ x ≤1 9. f(x) = |sin20πx|, 0≤ x ≤1 10. f(x) = , 0≤ x ≤1 11. f(x) = sin(sin20πx), 0≤ x ≤1 12. f(x) = sin(20π|x–0,5|x3), 0≤ x ≤1 13. f(x) = , 0≤ x ≤1 14. f(x) = , 0≤ x ≤1 15. f(x) = , 0≤ x ≤1 Задание 11 (5.1.1) Построить график функции с применением команды plot(t,y)
При построении графикa вид функции, пределы, шаг изменения аргумента выбрать с использованием следующих данных.
Задание 12 (5.1.1) Построить в одном окне графики двух функций y1(t) и y2(t) с использованием команды plotyy(…)
При построении графиков вид функций, пределы, шаг изменения аргумента выбрать с использованием следующих данных.
Задание 13 (5.1.1) С помощью командыplot(t,y1,'S1′,t,y2,′S2′) построить в одном окне графики двух функций y1(t) и y2(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′выбрать с использованием следующих данных.
Задание 14 (5.2.1) С помощью командыstem(t,y2,′S′) построить график функции y2(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′выбрать с использованием следующих данных.
Задание 15 (5.2.2) С помощью команды stairs(t,y1,′S′) построить график функции y1(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′ выбрать с использованием следующих данных. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2.
2.  3.
3. 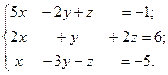
 5.
5.  6.
6. 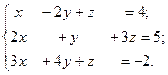
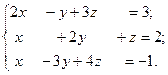 8.
8.  9.
9. 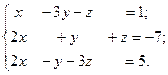
 11.
11. 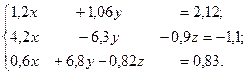
 13.
13. 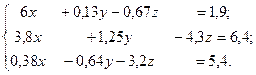
 15.
15. 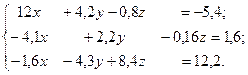










 квадратной матрицы с ее диагональю.
квадратной матрицы с ее диагональю. 2. f(x)=
2. f(x)=  3. f(x)=
3. f(x)= 
 5. f(x)=
5. f(x)= 
 7. f(x)=
7. f(x)= 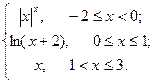 8. f(x)=
8. f(x)= 
 10. f(x)=
10. f(x)= 
 12. f(x)=
12. f(x)= 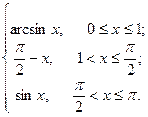
 14. f(x)=
14. f(x)= 
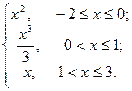
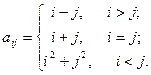
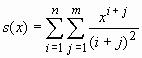 .
. .
.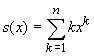 .
.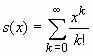
 , y2(t)=cos(20t)
, y2(t)=cos(20t)
 , y2(t)=
, y2(t)=  (10t)
(10t)
 (20t)
(20t)
 , y2(t)= cos(20t)
, y2(t)= cos(20t)
 (20t)
(20t)
 , y2(t)=sin(10t)
, y2(t)=sin(10t)
 ], ∆t=0,01
], ∆t=0,01
 -0,5t, tÎ[0;2
-0,5t, tÎ[0;2