
|
|
Обучение перцептронов с помощью a- и g-систем подкрепления12 Общие сведения
Перцептроны или персептроны (от perceptio – восприятие) были первыми искусственными нейронными сетями, появившимися в результате многолетних исследований мозга животных и человека. Автор первого перцептрона – американский ученый Френк Розенблатт, впервые опубликовавший свои исследования в этой области в 1957 году. По мнению Ф. Розенблатта, перцептроны, прежде всего, являются классом моделей мозга, объясняющих некоторые его характерные функции. В частности, перцептроны, пусть и в самой элементарной форме, объясняют некоторые проблемы организации памяти биологических систем, демонстрируют механизм приобретения знаний «познающих (cognitive) систем» об окружающем их мире и показывают, что эти знания зависят как от когнитивной системы, так и от окружающей среды. По Розенблатту, для различных видов животных простейшее представление об анатомической структуре нервной системы может быть получено с помощью схемы, представленной на рис. 2.1. Каждый из пяти видов информации о внешней среде воспринимается своими специализированными сенсорными нейронами и передается по своим отдельным сенсорным трактам в центральную нервную систему. Через моторные нейроны центральная нервная система связана с мышцами и железами организма. В своих первых работах Розенблатт рассматривал модель только зрительной системы. В наиболее простом виде эта модель включает в себя три последовательно соединенных множества нейронов: чувствительных (S-элемен-тов), ассоциирующих (A-элементов) и реагирующих (R-элементов). S-элементам в нервной системе животного или человека соответствуют сенсорные или рецепторные нейроны, генерирующие сигналы на поступающие внешние раздражения (изображения) и передающие их A-нейронам. A-элементы аналогичны в нервной системе живого организма нейронам, образующим локальный специализированный зрительный центр в коре головного мозга и связывающим рецепторные нейроны с моторными. R-элементам в нервной системе соответствуют эффекторные (моторные) нейроны, упорядоченные в ограниченные топологические структуры и передающие сигналы управления центральной нервной системы к мышцам и железам организма. Определение 2.1. S-элемент называется простым, если он выдает единичный выходной сигнал при входном сигнале, превышающем некоторый заданный порог Определение 2.2. Простым ассоциативным элементом называется A-эле-мент, который выдает единичный выходной сигнал, если алгебраическая сумма его входных сигналов превышает некоторый заданный порог
Определение 2.3. Простым биполярным (бинарным) реагирующим элементом называется R-элемент, выдающий единичный выходной сигнал, если алгебраическая сумма его входных сигналов больше или равна пороговому значению, и отрицательный единичный (нулевой) сигнал, если сумма его входных сигналов меньше заданного порога. Чувствительные S-элементы живого организма (рис. 2.2) возбуждаются от воздействия энергии света, если величины их входных сигналов превышают некоторый порог
Комбинация выходов всех A-элементов представляет собой реакцию двух первых слоев перцептрона на предъявленное входное изображение, которая с помощью выходного слоя нейронов преобразуется в необходимую комбинацию выходных сигналов системы. Часто требуют, чтобы каждому классу входных изображений соответствовал только один определенный активный R-нейрон. Необходимых комбинаций выходных сигналов на каждый класс изображений добиваются на этапе обучения или адаптации перцептрона за счет изменения переменных весов связей между A- и R-элементами. Разделение множества G изображений на два класса G1 и G2 можно выполнить с помощью одного выходного элемента. В этом случае изображениям первого класса может соответствовать положительный выходной сигнал (+1) R-элемента, а второго класса – отрицательный (–1). На примере простейшего (элементарного) перцептрона рассмотрим различные способы обучения этих нейросетей, впервые предложенные и исследованные Розенблаттом. Определение 2.4. Простым перцептроном называется нейронная сеть, состоящая из S-, A- и R-элементов и удовлетворяющая следующим пяти условиям: 1. В сети имеется только один R-нейрон, который соединен связями с переменными весами со всеми A-нейронами. 2. В сети имеются только последовательные связи от S- к A-элементам и от A-элементов к R-элементу. 3. Веса связей между S- и A-элементами являются фиксированными. 4. Время передачи сигналов каждой связью равно нулю (либо фикси-рованной постоянной величине). 5. Выходные сигналы всех нейронов сети формируются в виде:
где Определение 2.5. Простой перцептрон с простыми A- и R-элементами и передающими функциями связей вида:
где wij(t) – вес связи между i-м и j-м нейронами в момент времени t; Элементарный перцептрон обучается или настраивается на распознавание двух классов изображений G1, G2 путем предъявления ему некоторых последовательностей изображений из этих классов. Учитель (человек или вычислительная машина), наблюдающий реакцию перцептрона на каждое входное изображение, при наличии ошибочных решений сети должен корректировать веса связей между R- и A-элементами в соответствии с некоторой системой правил. Определение 2.6. Матрицей взаимодействия перцептрона называется матрица, элементами которой являются веса связей wij для всех пар нейронов Ui, Uj сети. Если связь между нейронами Ui, Uj отсутствует (например, в простом перцептроне нет связей между R- и S-нейронами), то принимают wij = 0. Матрица взаимодействия фактически отображает состояние памяти перцептрона. Множество всех возможных состояний памяти сети образует фазовое пространство сети, которое может быть представлено в виде области в n-мерном евклидовом пространстве, каждая координатная ось которого соответствует одной связи сети.
Обучение перцептронов с помощью a- и g-систем подкрепления
Определение 2.7. Системой подкрепления нейронной сети называется любой набор правил, с помощью которых можно изменять во времени состояние памяти сети (или матрицу взаимодействия). Определение 2.8. Положительным (отрицательным) подкреплением назы-вается такой процесс коррекции весов связей, при котором вес связи wij(t), начи-нающейся на выходе активного i-го элемента и оканчивающейся на входе j-го элемента, изменяется на величину Δwij(t), знак которой совпадает со знаком выходного сигнала j-го нейрона (знак которой противоположен знаку выходного сигнала j-го нейрона). Существует большое число различных систем подкрепления, большая часть из которых представляет лишь исторический интерес. Поэтому остановимся только на системе подкрепления с коррекцией ошибок, которая является основной в настоящее время. В системе подкрепления с коррекцией ошибок прежде всего необходимо определить, является ли реакция перцептрона правильной. До тех пор, пока выходной сигнал R-элемента принимает желанное значение, величина сигнала подкрепления η равна нулю. При появлении неправильной реакции перцептрона используется подкрепление, величина и знак которого в общем случае определяется монотонно возрастающей функцией f:
где R* – желаемая реакция; R – полученная реакция; f(0) = 0. Таким образом, при появлении ошибки для коррекции весов связей используется сигнал, знак которого противоположен знаку выходного сигнала R-элемента. В связи с этим рассмотренный метод коррекции весов получил название системы с отрицательным подкреплением. Конкретным примером системы подкрепления с коррекцией ошибок является альфа-система подкрепления. В этой системе при наличии ошибок веса всех активных связей, которые оканчиваются на R-элементе, изменяют на одинаковую величину η, а веса всех неактивных связей оставляют без изменений. Перцептроны, в которых применяется альфа-система подкрепления, называются альфа-перцептронами. При использовании альфа-системы подкрепления сумма весов всех связей между R- и A-нейронами может возрастать (или убывать) от шага к шагу, что должно приводить к нежелательным ситуациям, когда многие связи имеют максимальные (или минимальные) веса и не могут использоваться в дальнейшем процессе обучения нейронной сети. Для устранения этого недостатка α-системы подкрепления была предложена гамма-система подкрепления, которая обладает свойством консервативности относительно суммы Σ1 весов всех связей между нейронами, т.е. сумма Σ1 остается постоянной в процессе обучения перцептрона. Это достигается за счет того, что при наличии ошибочной реакции перцептрона сначала веса всех активных связей изменяются на одинаковое значение η, а вслед за этим из весов всех активных и пассивных связей вычитается величина, равная отношению суммы изменения весов всех активных связей к числу всех связей. Изменение весов отдельных связей при этом определяется соотношением:
где Δwij – в общем случае приращение веса связи между i-м A-нейроном и j-м R-нейроном, для элементарного перцептрона j = const = 1; η – величина сигнала подкрепления; Nак – число активных связей; N – число связей, оканчивающихся на входе j-го элемента. При такой системе коррекции весов связей выполняется равенство:
из которого и следует консервативность гамма-системы подкрепления относи-тельно суммы весов всех обучаемых связей. Замечание 2.1. Отметим, что соотношение (2.2) в неявной форме предпо-лагает, что корректируемые веса wij связей достаточно далеки от своих граничных значений wij min= 0 и wij max =1, т.е.
Если неравенства (2.3) нарушаются, а требование консервативности относительно суммы Σ1 весов связей остается неизменным, то соотношение (2.2) необходимо уточнить. Пусть, например, среди активных связей Nа гр. связей имеют граничные значения весов
Пусть также Nа бгр. активных связей имеют веса, близкие к граничным, для которых справедливы неравенства
В этом случае общая сумма Sa первоначальных изменений весов активных связей будет равна:
где Если предположить, что для всех пассивных связей выполняются соотношения (2.3), тогда из весов пассивных связей и весов активных связей, для которых не выполняется соотношение (2.4) или (2.5), вычитается величина
Примером еще одного общего способа обучения перцептронов является метод коррекции ошибок случайными возмущениями. Он предусматривает, как и альфа-система подкрепления, при появлении ошибок – коррекцию весов активных связей, но знак и величина коррекции для каждой связи выбирается случайно в соответствии с некоторым заданным распределением вероятностей.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , и нулевой сигнал – в противном случае.
, и нулевой сигнал – в противном случае.











 – алгебраическая сумма сигналов, поступающих одновременно на вход нейрона.
– алгебраическая сумма сигналов, поступающих одновременно на вход нейрона.
 – выходной сигнал i-го нейрона в момент времени
– выходной сигнал i-го нейрона в момент времени  ;
;  – время передачи сигнала
– время передачи сигнала  (2.1)
(2.1) (2.2)
(2.2)
 (2.3)
(2.3) или
или  и для них выполняются условия
и для них выполняются условия (2.4)
(2.4) (2.5)
(2.5) , (2.6)
, (2.6) – граничное значение веса связи между k-м и j-м нейронами,
– граничное значение веса связи между k-м и j-м нейронами,  ;
; 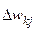 – приращения веса связи, определяемое по соотношению (2.2) без учета наличия множества
– приращения веса связи, определяемое по соотношению (2.2) без учета наличия множества  – знаковая функция.
– знаковая функция. . С учетом этих замечаний соотношение (2.2) принимает вид:
. С учетом этих замечаний соотношение (2.2) принимает вид: