
|
|
Средние значения плотности rИ кинематической вязкости n некоторых жидкостей
Примечание. Плотность жидкости при другой температуре можно определить по формуле ГИДРОДИНАМИКА
Гидродинамика – раздел гидравлики, в котором рассматриваются законы движения жидкости и взаимодействие с твердыми телами в результате ее движения.
Основные понятия
Гидродинамическое давление – давление внутри жидкости при ее движении. Линия тока – кривая, для которой векторы скоростей принадлежащих ей в данный момент времени частичек жидкости являются касательными к данной кривой. Трубка тока – цилиндрическая или коническая поверхность, образованная совокупностью линий тока, проведенных через контур, ограничивающий элементарную площадку Элементарная струйка – жидкость, движущаяся внутри трубки тока. Живое сечение потока Смоченный периметр П – длина контура живого сечения, по которому жидкость соприкасается со стенками, ограничивающими ее движение. Гидравлический радиус RГ : Эквивалентный диаметр dЭ : Расход - массовый расход, кг/с, т/ч; - объемный расход, м3/с, м3/ч. Средняя скорость – фиктивная, одинаковая для всех частиц жидкости данного сечения скорость, определяемая как отношение объемного расхода к площади данного живого сечения: Движение жидкости можно классифицировать следующим образом: а) Установившееся и неустановившееся. Если гидродинамическое давление и скорость жидкости изменяются в данной точке пространства в зависимости от координат и времени, то движение неустановившееся. б) Напорное и безнапорное. Безнапорное движение наблюдается при наличии у жидкости свободной поверхности (границы раздела жидкости с воздухом окружающей среды) и происходит под действием только силы тяжести. При напорном движении жидкость полностью заполняет поперечное сечение канала. Напорное движение осуществляется за счет разности давления в начале и конце канала и под действием гидродинамического давления, создаваемого насосом. в) Равномерное, неравномерное и плавноизменяющееся движение. Установившееся движение может быть равномерным и неравномерным. При равномерном движении средняя скорость и площадь живого сечения потока не изменяются по длине. При неравномерном движении – изменяются по длине. Плавноизменяющееся – такое неравномерное движение, при котором радиус кривизны линий тока очень велик, угол расхождения очень мал, живые сечения струек – плоские площадки, нормальные к оси потока.
Уравнение неразрывности
Для жидкости, текущей вдоль стенок, ее ограничивающих, можно применить закон сохранения материи, из которого следует: количество втекающей жидкости в канал равно количеству жидкости, из него вытекающей, то есть расход – величина постоянная для любого сечения участка канала:
Это уравнение носит название уравнения неразрывности. Его можно преобразовать в следующее:
Уравнение Бернулли для элементарной струйки Идеальной жидкости
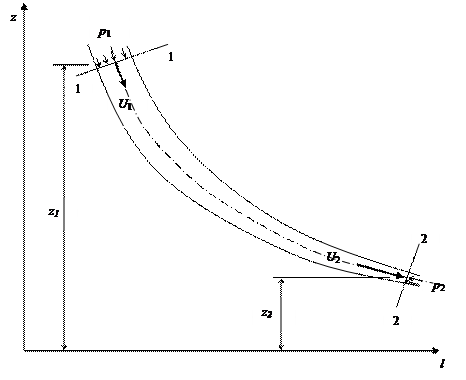
Если применить закон сохранения энергии для единицы массы стационарно движущейся идеальной жидкости, то можно сделать вывод: и в сечении 1-1 и в сечении 2-2 (рис. 17) жидкость обладает одинаковой удельной (отнесенной к единице массы) энергией.
Рис. 17
где gz (
Изменение одной составляющей удельной энергии движущейся жидкости приводит к противоположному изменению других составляющих. Уравнение Бернулли можно записать в следующем виде (разделим все члены уравнения на ускорение свободного падения g):
Первое слагаемое z представляет собой геометрический напор – высоту расположения потока над нулевой плоскостью. Второе – пьезометрический напор p/(rg) – расстояние от центра тяжести живого сечения до уровня жидкости в пьезометре. По уровню определяют давление жидкости в данном сечении. Третье – скоростной напор
Рис. 18
Таким образом, сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль потока идеальной жидкости. В этом заключается геометрическая интерпретация уравнения Бернулли (рис. 19). Напорная линия, проходящая по уровням жидкости в трубках Пито, представляет собой горизонтальную прямую. Тогда как линия, проходящая по уровням жидкости в пьезометрах, или пьезометрическая линия, может располагаться различными способами, в зависимости от формы и расположения канала. Умножив все члены уравнения (3) на r, получим уравнение Бернулли, все члены которого выражены в единицах давления (Па):
где rgz – весовое давление, p – гидромеханическое давление, или просто давление,
Рис. 19

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где
, где 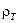 – плотность жидкости при температуре
– плотность жидкости при температуре 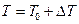 ;
;  – изменение температуры;
– изменение температуры;  – температура, при которой плотность жидкости равна
– температура, при которой плотность жидкости равна  ,
,  – коэффициент температурного расширения жидкости (в среднем для минеральных масел можно принять
– коэффициент температурного расширения жидкости (в среднем для минеральных масел можно принять  .
. – площадь сечения потока жидкости, проведенная перпендикулярно линиям тока.
– площадь сечения потока жидкости, проведенная перпендикулярно линиям тока.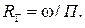
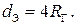
 – количество жидкости, протекающее через живое сечение в единицу времени. Различают:
– количество жидкости, протекающее через живое сечение в единицу времени. Различают: .
. . Из определения средней скорости следует:
. Из определения средней скорости следует: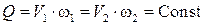
 .
.
 , (3)
, (3) ) – удельная потенциальная энергия положения
) – удельная потенциальная энергия положения (
( 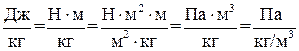 ) – удельная потенциальная энергия давления
) – удельная потенциальная энергия давления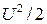 (
(  ) – удельная кинетическая энергия.
) – удельная кинетическая энергия. ,
, . Определяется как разность уровней жидкости в трубке Пито и пьезометре (Рис.18). По показаниям трубки Пито определяются два слагаемых в уравнении Бернулли
. Определяется как разность уровней жидкости в трубке Пито и пьезометре (Рис.18). По показаниям трубки Пито определяются два слагаемых в уравнении Бернулли  (рис. 18).
(рис. 18).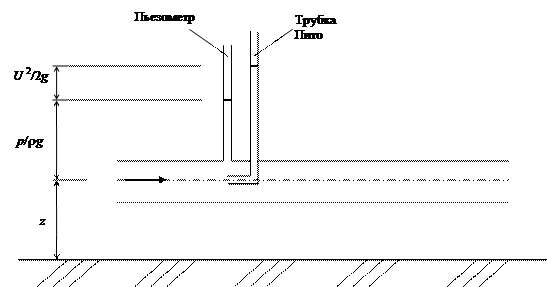
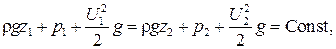

 – динамическое давление.
– динамическое давление.