
|
|
Для выхода из предкризисного состояния необходимо уменьшить срок работ по текущему проекту на 3 недели (затраты на ускорение работ в последнем столбце таблицы)Недостатки • дублирование ресурсов. Оборудование и персонал не используются в разных проектах; • игнорируются организационные цели и политика предприятия, поскольку члены групп часто как психологически, так и физически перемешаются из одного подразделения в другое; • вследствие ослабления связи функциональных подразделений организация запаздывает с освоением новых технологий; • поскольку члены групп не имеют "родной" функциональной зоны, их беспокоит, что они будут делать после завершения проекта, что нередко приводит к затягиванию сроков его выполнения. Функциональный проект. Полной противоположностью предыдущей организационной структуре является функциональный проект(Functional Project). Он характеризуется тем, что проект осуществляется в существующих функциональных подразделениях. Преимущества: · члены проектной группы могут одновременно работать над несколькими проектами; · технический опыт сохраняется в пределах конкретной функциональной зоны, даже если участник проекта покидает группу или увольняется из организации; · функциональная зона остается "родной" для участников проектной группы даже после реализации проекта. Функциональные специалисты могут продвигаться вверх по службе; · в следствие насыщенности группы высокопрофессиональными специалистами из нескольких функциональных зон повышается эффективность решения различных технических проблем, связанных с проектом. Недостатки: - аспектам проекта, не связанным непосредственно с конкретной функциональной зоной, уделяется недостаточно внимания; - мотивация командной работы часто очень слаба; - потребности клиента носят вторичный характер, и реакция на них замедлена. Матричный проект. Классическая матричнаяорганизационная форма характеризуется тем, что в ней объединяются качества структур как обособленного, так и функционального проектов. В каждом таком проекте задействованы люди из разных функциональных зон. Менеджер проекта (Project Manager — РМ) принимает решения относительно того, какие задания и когда должны выполняться, а функциональные менеджеры решают, какие именно люди будут заниматься этой работой и какие технологические приемы следует применять. Преимущества: - усиливается взаимосвязь между функциональными различными подразделениями; - менеджер проекта несет ответственность за его успешную реализацию; - дублирование ресурсов сводится к минимуму; - функциональная зона остается "родной" для членов проектной группы даже после завершения проекта, поэтому они менее обеспокоены своей судьбой после его окончания, чем при такой организационной структуре, как обособленный проект; - деятельность по реализации проекта согласуется с политикой основной организации, что усиливает поддержку проекта. Недостатки: - появляются два руководителя, и зачастую мнение функционального менеджера выслушивается прежде, чем мнение менеджера проекта. При такой ситуации, кроме всего прочего, трудно сказать, кто из них важнее для продвижения конкретного человека по службе. - проект обречен на неудачу, если менеджер проекта лишен таланта успешно вести переговоры; - определенную опасность таит в себе то, что менеджеры проектов стремятся иметь запас ресурсов для своих проектов, нанося тем самым вред другим программам компании. Обратите внимание, что независимо от того какая структура именно выбрана, непосредственный контакт с заказчиком осуществляется через менеджера проекта. Следует помнить, что взаимодействие и скорость реакции на запросы потребителя резко повышаются, если за успех проекта отвечает один человек. 10.2.Сетевой график Понятие сетевого графика относится к набору графических методов, используемых при планировании хода проекта и наблюдении за ним. Для любого типа проекта основными факторами являются время, затраты (издержки) и наличие ресурсов. Сетевые методы были разработаны для планирования и отслеживания всех этих факторов, как по отдельности, так и в различных комбинациях. Наиболее известными методами составления сетевого графика являются PERT (Program Evaluation And Review Technique — метод оценки и пересмотра программ) и СРМ (Critical Path Method — метод критического пути) Оба они разработаны в 50-х годах. СРМ является детищем ученых Дж. И. Келли (J Е. Kelly, компания Remington-Rand) и М. Р. Уокера (М. R. Walker, компания Du Pont), его создание относится к 1957 году. Данный метод изначально использовался как вспомогательный инструмент, применяемый при составлении графиков проведения технического обслуживания на химических заводах. Метод PERT был создан в 1958 году под эгидой Управления специальных проектов ВМС США (U.S Navy Special Projects Office) как инструмент для составления графика и контроля за ходом работ при разработке ракета Polaris. В компании Boeingметоды эффективного управления проектами играли чрезвычайно важную роль как в процессе разработки сборочно-монтажной схемы 777, так и при календарном планировании работ и в производственном процессе. Заметим, что 20% самолетов модели 777 строятся в Японии, а комплектующие поставляются другими странами Австралией (рулевое управление), Северной Ирландией и Сингапуром (передние опоры шасси), Кореей (законцовки крыла), Бразилией (здесь проводится сборка законцовок крыла и хвостового оперения) и Италией (внешние закрылки). Используя упомянутые выше методы, проект легко представить в графической форме, и его отдельные задания связываются между собой таким образом, чтобы основное внимание было сосредоточено на важнейших для выполнения проекта моментах. Чтобы методы составления графика критического пути можно было применить с наибольшей эффективностью, проект должен обладать следующими характеристиками: 1. В нем должны быть точно определены операции или здания, которые обозначают начало и окончание проекта. 2. Задания или операции должны быть взаимно независимы. Необходимо, чтобы в пределах определенной последовательности их можно было начинать, приостанавливать, исключать и выполнять независимо один от другого. 3. Необходимо наметить точный порядок выполнения операций и заданий; они должны выполняться в определенной последовательности. Перечисленные выше свойства проектов характерны для таких отраслей промышленности, как строительство, самолетостроение и судостроение, поэтому методы сетевых графиков применяются в них особенно широко. Кроме того, как мы уже упоминали, эти методы и другие принципы управления проектами все чаще используются фирмами, которые работают в отраслях промышленности, имеющих тенденцию быстро меняться. Временные модели. В своих базовых формах методы PERT и СРМ предназначены для определения наиболее длительного по времени пути в цепи работ, которые становится основой при планировании и контроле за ходом выполнения проекта. Для графического отображения этой последовательности в обоих методах применяются линии со стрелками и узлы. Изначально PERT и СРМ отличались между собой тем, что в сетевом графике PERT операция обозначалась стрелкой, а в СРМ — узлом (кружком). Существовало и еще одно различие: в PERT использовались три типа оценки продолжительности операций (оптимистическая, пессимистическая и наиболее вероятная), а в СРМ — только наилучшая. Эти различия объясняются тем, что метод PERT разрабатывался для работы со сложными проектами, которые характеризуются высокой степенью неопределенности, а СРМ — для составления графиков рутинных операций, связанных с заводским техническим обслуживанием. За долгие годы существования этих двух методов различия между ними стерлись, поскольку пользователи СРМ начали также применять три оценки продолжительности операций, а в сетевых графиках PERT операции нередко обозначаются узлами. По сути, оба эти метода обязаны своим появлением их широко известному предшественнику, графику Ганта. График Ганта позволяет привязать операции ко времени. Однако в проектах с числом операций 25—30, график оказывается слишком громоздким для визуального восприятия. Кроме того, график Ганга не располагает прямой процедурой для определения критического пути, но, несмотря на ряд таких недостатков, он имеет огромное практическое значение. Основные характеристики сети и их расчет. Итак, пусть дуги — это работы, а узлы — это события. Дуге, идущей из i-го события в j-ое, приписывается время выполнения работы ti,j , которую эта дуга символизирует. Конечно, времена выполнения работ могут быть неизвестны. В этом случае с помощью экспертизы (о ней речь будет идти ниже) определяют минимальное (оптимистическое) время а , максимальное (пессимистическое) времяb, наиболее вероятное время m и считают расчетное время по формуле:
Оценка tтем точнее, чем ближе друг к другу aи b. На рис.11.3 показана сеть из дуг и узлов, каждой дуге соответствует время выполнения работы в неделях, изображенное в прямоугольнике этой дуги.
 
Рис.10.3. Сеть и ее элементы (PERT). Так, дуга (стрелка) 0-1 соответствует некоторой работе (операции), которая может быть выполнена за 3 недели. Чтобы конкретно вести какие-либо расчеты, необходимо, прежде всего, пронумеровать события. Делается это так: находится исходное событие (в него не входит ни одна операция), ему присваивается номер 0 (или 1). Далее вычеркиваются все операции, выходящие из 0-ой и появляется хотя бы одно событие, в которое не входит ни одна работа (появляются новые «исходные» события). Этим событиям присваивают следующие по порядку номера 1, 2 и т. д. После чего снова вычеркивают дуги, выходящие из вновь перенумерованных вершин и т. д., пока все работы не будут перенумерованы. Двигаясь из начального события к конечному событию, мы можем проходить разные маршруты. Время движения по каждому маршруту свое (хотя, конечно, на некоторых маршрутах время может быть и одинаковым). Максимальное время прохождения какого-либо маршрута называют полным временемосуществления проекта. Любой путь, время движения по которому равно полному времени осуществления проекта, называют критическим путем. Предполагая, что исходное событие (0)происходит в нулевой момент, можно найти ранние сроки свершения событий:ранний срок свершения события (0)будет E(0) = 0, ранний срок свершения события (1)будет Е(1) = E(1) + t0,1 (в нашем примере Е(1) = 0 + 3 = 3)и т.д. Если в событие входит несколько работ, то расчет усложняется. Пусть в i-ое событие входят работы k, р, ..., z. Находим все суммы E(k) + tki, E(p) + tpi, ..., Е(z) + tzi. Ясно, что Е(i) будет равно максимальнойиз найденных величин, поскольку событие свершится только после завершения последней, самой поздней работы. В нашем примере в четвертую вершину идут три стрелки. Зная E(1),E(2), Е(3) и t14, t24, t34, находим: Е(1) + t14= 7, Е(2) + t24 = 6, E(3) +t34 = 6. Пятое событие не может свершиться ранее седьмого момента времени. Ранний срок свершения события, как мы видим, определяется длиной максимального пути от исходного события к конечному. Раннее время свершения последнего события как раз и дает полное время осуществления проекта. Следующая важная характеристика для сети — поздний срок наступления события,определяемый как последний момент времени, в который еще может произойти событие при условии: неизменности полного времени выполнения проекта. Для конечного события поздний и ранний сроки равны. Поздний срок свершения событияL(j) находят подобно раннему сроку, но двигаются из конца сети в начало. Например, событие 2должно произойти не позже L(2) = L(4) – t24 = 5. Для нахождения L(j)берут все вершины, в которые входят работы из j-ой вершины (пусть это будут вершины k, p, ...,z),находят все разности L(k) — tj,k , L(p) – tj,p, .., L(z) –tj,z ,самая минимальная из которых и дает L(j).За поздний срок завершающего события берется его ранний срок свершения. В примере L(4) = E(4) = 7, L(3) = L(4) – t 34 = 6 (здесь только одна работы); для первой вершины надо уже сравнить L(4) – t14=3 и L(3) – t13 = 4. Видим, что L(1) = 3 (так как в противном случае возрастает общее время выполнения проекта). Конечно, ранний срок свершения события не больше позднего срока. У всех событий критического пути (то есть пути с максимальным временем) ранние и поздние сроки свершения совпадают, но кроме этого продолжительность каждой работы критического пути равна разности между моментами свершения конечного и начального события этой работы. Проверка этих двух условий лежит в основе программ для ЭВМ, рассчитывающих критические пути. Для нашего примера критическим будет путь 0 — 1 — 4 (он показан утолщенными стрелками- работами). Если работа не лежит на критическом пути, то у нее есть определенный резерв времени, что очень важно для поиска эффективного распределения ресурсов по работам. Резервы бывают общие, свободные и независимые. Пусть работа, связывающая события (i), (j),имеет продолжительность ti,j, L(j) — поздний срок для j-го события, E(i) — ранний срок для i-го события. Общий резерв(иногда называемый полным резервом) Ri,j = L(j) - E(i) – ti,j — это то время, на которое можно перенести начало работы, не увеличивая общее время выполнения проекта. В нашем примере R13 = L(3) - E(1) – t13 = 0. Свободный резерввремени ri,jработы ij вычисляется так: ri,j = E(j) -E(i) – ti,j.Этот резерв — часть общего резерва; ri,j -показывает, на сколько можно отодвинуть начало работы ijот раннего момента ее возможного начала, не влияя на наступление раннего срока свершения (j)(которое наступает после выполнения работы ij).В нашем примере r1,3 = E(3)-E(1) – t13= 0; r24= E(4)- E(2)- t24. Важно понимать, что использование резерва одной работы может уменьшать резервы последующих или предыдущих работ. Иногда (но только иногда!) продолжительность времени выполнения работы может быть увеличена без изменения резервов времени предшествующих и последующих работ. Такое возможное увеличение времени работы и называется независимым резервом времени работы.Вычисляется независимый резерв времени работы так: Pi,j = E(j) - L(i) – ti,j, если получается положительная величина, и ноль — в противном случае. Зная, что работа обладает некоторым (ненулевым) независимым резервом, можно уменьшить выделяемый ей ресурс (в разумных пределах, укладываясь в этот резерв). При этом мы не увеличиваем общее время выполнения проекта, более того, высвободившийся ресурс можно передать какой-нибудь работе на критическом пути, и уменьшить общее время выполнения проекта. В нашем примере Р1,3= E(3) – L(1)- t1,3 (при t1,3= 2), значит, Р1,3= 0. Если бы было t1,3= 1, то получили бы Р1,3 = 1.
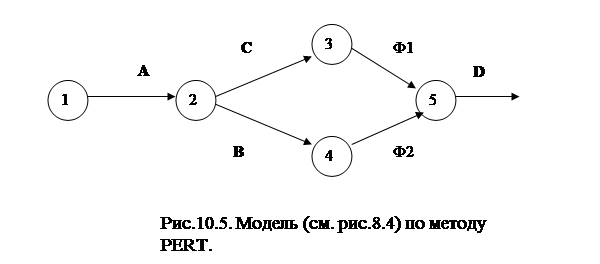
10.3. Сетевой график с однозначной оценкой продолжительности операций по методу СРМ. Предлагаем вашему вниманию простой пример составления сетевого графика проекта. Обратите внимание, что продолжительность каждой операции в данном случае указывается с использованием однозначной, т.е. наиболее вероятной, оценки (а не трех оценок, которые мы обсудим позднее) Обозначим операции латинскими буквами A, B, C, D в узлах ( кружках), а стрелки (дуги) показывают последовательность выполнения операций. В таблице 10.1 приводятся исходные данные сетевой модели, а на рис.10.4 представлена сетевая модель. Таблица 10.1 Исходные данные
* по методу PERT. Ниже представлено графическое изображение модели по данным табл. 10.1.
 
Здесь сверху кружочков- работ записано время выполнения работы. Снизу стрелок показано время начала работы. Критический путь 2+ 5 + 3 = 10 (единиц времени). На пути А-С-D имеем 2 + 4 +3 = 9, то есть резерв времени равен 10- 9 = 1. Для сравнения изобразим эту сетевую модель (см. рис.10.4) по методу PERT (см. рис.10.5 и табл.10.1), где Ф1 и Ф2 – фиктивные работы с временем исполнения и затратами равными нулю, или например, дуга (стрела) 2-3 есть операция или работа С(см. табл. 10.1).
10.4. Три оценки продолжительности операций. В этом примере продолжительность каждой операции устанавливается на основе трех оценок. Решение. 1. Составьте перечень всех операций, которые нужно выполнить в ходе проекта. 2. Определите последовательность выполнения этих операций и постройте сетевой график, отображающий эту последовательность. 3. Для определения продолжительности операций используются три следующие оценки: а — оптимистическая оценка продолжительности: минимальный реальный период времени, в течение которого может быть выполнена операция. (Существует очень небольшая вероятность, которая обычно оценивается как 1 %, что данная операция будет завершена в более короткие сроки); m — наиболее вероятная оценка продолжительности: наиболее точное предположение периода времени, необходимого для выполнения конкретной операции. Поскольку m является наиболее вероятной продолжительностью, это значение представляет собой также моду β - распределения; b — пессимистическая оценка продолжительности: максимальный реальный период времени, в течение которого операция должна быть выполнена. (Существует очень небольшая вероятность, которая обычно оценивается как 1%, что выполнение данной операции займет больше времени). Как правило, эти оценки даются непосредственными исполнителями конкретной операции. Вычислите ожидаемое время (Expected Time — ЕТ) каждой операции. Оно рассчитывается по формуле (1). Этот расчет основан на статистической концепции β - распределения, согласно которой наиболее вероятная оценка продолжительности операции (m) весит в 4 раза больше, чем оптимистическая (а) или пессимистическая (b) оценки продолжительности. β- распределение вероятностей отличается универсальностью, оно может принимать разные формы и в упрощенной версии, позволяет прямо вычислять среднее значение операции и среднеквадратическое отклонение. Определите критический путь. Критический путь определяется так же, как в обсужденном нами примере для однозначной оценки продолжительности операций, но с использованием значений ожидаемого времени. Вычислите дисперсию (σ2) продолжительности операции. Дисперсия (σ2) для ожидаемого времени каждой операции вычисляется по формуле.
Как видно, дисперсия представляет собой квадрат разности двух крайних значений продолжительности времени, разделенной на 6. Таким образом, очевидно, что, чем больше эта разница, тем больше значение дисперсии. Определите вероятность завершения проекта в назначенный срок. Использование трех оценок продолжительности операций дает возможность оценивать степень неопределенности срока завершения npoекта. Это осуществляется следующим образом: a) сложите значения дисперсий всех операций, расположенных на критическом пути. (Случаи, когда для проекта определено больше одного критического пути, описаны в следующем примере); b) подставьте это значение, а также назначенный срок окончания проекта и ожидаемое время завершения проекта в формулу аргумента функции Лапласа Z, которая имеет следующий вид:
где D — назначенный срок окончания проекта; Te — ожидаемое время завершения проекта. Ожидаемое время завершения проекта — это сумма продолжительностей всех операций, расположенных на критическом пути;
c) вычислите значение аргумента Z; d) используя значение Z, определите вероятность завершения проекта в назначенный срок (для этого следует воспользоваться таблицей нормального распределения вероятностей). Результаты выполнения всех описанных выше действий для нашего примера приведены в табл.10.3. Таблица 10.3 Ожидаемое время и дисперсии для операций A-G.
Рис. 10.6. Метод СРМ. Критический путь определяется так же, как было описано выше, и его продолжительность используется по тому же назначению. Здесь, цифры над кружком (операцией) показывают продолжительность работы, цифры возле стрелки показывают время окончания предыдущих операций. Конечная операция G заканчивается со временем 36+2=38. Основное различие между методом однозначной оценки продолжительности операций и методом с тремя оценками (оптимистической, наиболее вероятной и пессимистической) заключается в том, что во втором случае можно определить степень вероятности завершения проекта в заданные сроки. Поскольку в данном сетевом графике два критических пути A-C-F-G и A-B-D-F-G, необходимо принять решение, какие дисперсии следует использовать, чтобы максимально точно определить вероятность выполнения проекта в заданный срок. Традиционный подход заключается в использовании пути с наибольшей суммарной дисперсией, поскольку в этом случае внимание управленческого персонала будет направлено на операции, которые имеют большой разброс оценок продолжительности, а значит и обширную дисперсию. Следовательно, в нашем примере для определения вероятности завершения проекта должны быть использованы дисперсии операций А, С, F и G. Таким образом,
В соответствии с Приложением A находим, что значению Z= -0,87 соответствует вероятность 0,19. Это означает, что менеджер проекта имеет лишь 19%-ный шанс выполнить проект в 35-недельный срок. Обратите внимание, что данная степень вероятности характеризует, по сути, только критический путь A-C-F-G. Поскольку в сетевом графике есть еще один критический путь, а также другие пути, которые в ходе реализации проекта тоже могут стать критическими, фактическая вероятность выполнения проекта за 35 недель будет меньше 0,19. 10.5. Решение задачи с оптимизацией . Для выхода из предкризисного состояния необходимо уменьшить срок работ по текущему проекту на 3 недели (затраты на ускорение работ в последнем столбце таблицы)
С учетом данных продолжительности работ, стоимости их выполнения (данные представленные в таблице) предложите собственный вариант Решение (метод PERT).
Критический путь (работа на критическом пути). Время выполнения работ – 19 недель Чтобы сократить время, необходимо посмотреть стоимость ускорения работ на участках критического пути 1-3, 3-4, 4-6. Наименьшая стоимость будет на участке 4-6, потому сократим время выполнения с 5 недель до 2 недель с дополнительной стоимостью 3*5 = 15 тыс. грн. Весь проект будет выполнен за 16 недель и критических путей будет два (второй – 1-3, 3-5, 5-6 тоже 16 недель).
10.6. Что следует учитывать при использовании методов PERT и СРМ При проведении анализа с использованием методов PERT и СРМ приходится основываться на определенных допущениях. В этом разделе вашему вниманию предлагается описание некоторых из этих допущений и пояснения к ним. Один из наиболее сложных для управленческого персонала моментов связан с пониманием статистических методов, на которых основан анализ с использованием трех оценок продолжительности операций. Следовательно, менеджерам следует позаботиться о том, чтобы люди, ответственные за управление и наблюдение за ходом выполнения той или иной операции, разбирались в этих статистических приемах. 1. Допущение. Для каждой операции существуют точно определенные начальное и конечное положения на оси времени. Пояснение. Содержание проектов, особенно сложных, в ходе выполнения изменяется, вследствие чего временное положение операций в сетевом графике отличается от первоначального. Кроме того, сам факт точного определения продолжительности операций и построения сетевого графика свидетельствует об ограничении гибкости, необходимой для того, чтобы успешно управлять изменениями в ходе выполнения проекта. 2. Допущение. Существует возможность выстроить цепь последовательности операций проекта и определить взаимосвязи между операциями. Пояснение. Последовательность операций не всегда можно точно определить заранее. Определение порядка выполнения последующих операций зависит от выполнения предыдущих и по ходу выполнения проекта приходится пересматривать последовательности операций. Методы PERT и СРМ, в своей базовой форме, не обеспечивают возможности решения данной проблемы, но в последнее время разработан ряд новых методов, позволяющих менеджерам находить несколько вспомогательных, непредвиденных путей с учетом фактических отклонений по каждой отдельной операции. 3. Допущение. Продолжительность проекта определяется критическим путем и основное внимание при осуществлении проекта менеджер должен уделять ему. Пояснение. Утверждение, что общий срок завершения проекта определяется критическим путем с наибольшей продолжительностью (или путем с нулевым резервом времени), полученным в результате сложения значений ожидаемого времени операций, не всегда справедливо. В ходе выполнения проекта нередко случается, что какая-либо операция, не находящаяся на критическом пути, откладывается настолько, что это приводит к увеличению срока всего проекта. По этой причине было предложено концепцию критического пути заменить концепцией "критической операции" как основного фокуса усилий менеджера. При таком подходе внимание будет сконцентрировано на тех операциях, которые обладают высокой потенциальной возможностью отклонения и лежат на пути, "близком к критическому". Другими словами, может существовать такой путь, который включает операции с некоторым резервом времени и который может стать критическим, если будет задержано выполнение одной или нескольких лежащих на нам операций. Очевидно, что чем выше степень параллельности в сетевом графике, тем выше вероятность существования одного или нескольких путей, близких к критическому. И наоборот, чем больше сетевой график приближен к одной цепочке операций, тем меньше вероятность, что в нем будет путь такого рода. И наконец, скептическое отношение к использованию сетевых методов в управлении проектом часто основывается на их стоимости Правда, следует заметить, что стоимость применения методов PERT и СРМ редко превышает 2% обшей стоимости проекта Если к такому анализу добавляется составление различных отчетов и структуры работ проекта, он становится несколько дороже, но и в этом случае стоит не больше 5% общей стоимости проекта Однако эти дополнительные расходы обычно полностью компенсируются экономией, которая достигается благодаря составлению более точного и гибкого графика и сокращению сроков выполнения проекта. Резюме. 1. Проектможно определить как последовательность взаимосвязанных операций, направленных, как правило, на достижение конкретного значительного результата, и для их выполнения требуется достаточно продолжительное время 2. Проекты обычно рассматриваются как самостоятельный процесс, однако на практике многие проекты могут повторяться и просто переноситься в другие условия или на другие виды продукции, чем достигается совершенно иной результат 3. Каждый проект состоит из следующих этапов: составленияперечня работ,рабочего задания,конструкторской разработки; изготовления опытного образца; испытания опытного образца; изготовления и приемки опытной партии. 4. Понятие сетевого графика относится к набору графических методов, используемых при планировании хода проекта и наблюдении за ним. Для любого типа проекта основными факторами являются время, затраты (издержки) и наличие ресурсов. Сетевые методы были разработаны для планирования и отслеживания всех этих факторов, как по отдельности, так и в различных комбинациях. 5. Любой путь, время движения по которому равно полному времени осуществления проекта, называют критическим путем. 6. Эффективное управление проектами значительно более сложный процесс, чем простое использование графиков PERT и СРМ. Оно требует четкого распределения ответственности за выполнение тех или иных работ, четкой системы своевременной подачи отчетов о ходе проекта и правильного управления персоналом 7. Существуют причины, по которым проект может "провалиться" Наиболее серьезная из них заключается в недостаточном внимании к фазе планирования. Кроме того, выполнение проекта, как правило, заканчивается неудачей, если проектная группа хоть и доверяет своему руководителю, но не выполняет его требований, а также, если в команде нет талантливого менеджера. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
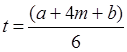 . (10.1)
. (10.1)

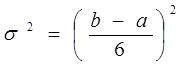 (10.2)
(10.2) (10.3)
(10.3) — сумма дисперсий продолжительностей операций, лежащих на критическом пути;
— сумма дисперсий продолжительностей операций, лежащих на критическом пути;
 7 8
7 8

 21 28
21 28
 21 36 2
21 36 2



 5 2 28 5
5 2 28 5
 21
21 σcp2 =9 + 2,78 + 0,11 + 0 = 11,89. Предположим, что менеджер хочет узнать, насколько вероятно завершить реализацию проекта за 35 недель, т.е. D = 35. Раньше было определено, что ожидаемое время окончания проекта составляет 38 недель. Подставив эти значения в формулу Z, получаем Z = -0,87.
σcp2 =9 + 2,78 + 0,11 + 0 = 11,89. Предположим, что менеджер хочет узнать, насколько вероятно завершить реализацию проекта за 35 недель, т.е. D = 35. Раньше было определено, что ожидаемое время окончания проекта составляет 38 недель. Подставив эти значения в формулу Z, получаем Z = -0,87.