
|
|
Первое уравнение Максвелла12 Лекция 17/10 ОСНОВЫ ТЕОРИИ МАКСВЕЛЛА 1. Теория Максвелла - теория единого электромагнитного поля
Теория Максвелла - это последовательная теория единого электромагнитного поля, которое создается произвольной системой электрических зарядов и токов. В теории Максвелла решается основная задача электродинамики: по заданному распределению зарядов и токов вычисляются характеристики создаваемого ими электрического и магнитного полей. Теория Максвелла – это обобщение важнейших законов, описывающих электрические и магнитные явления: теоремы Гаусса, закона полного тока, закона электромагнитной индукции. Эта теория не рассматривает внутренний механизм явлений, происходящих в среде и вызывающих появление электрических и магнитных полей. Среда описывается с помощью трех величин, задающих ее электрические и магнитные свойства: относительной диэлектрической проницаемости Рассматриваются макроскопические поля, которые создаются макроскопическими зарядами и токами, сосредоточенными в объемах, много больших объемов атомов и молекул. Расстояния от источников полей до рассматриваемых точек пространства много больше линейных размеров атомов и молекул. Поэтому макроскопические поля изменяются заметно лишь на расстояниях, много больших размеров атомов. Макроскопические заряды и токи являются совокупностями микроскопических зарядов и токов, которые создают свои электрические и магнитные микрополя. Эти микрополя непрерывно меняются с течением времени в каждой точке пространства. Макроскопические поля – это усреднение микрополя. Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия осуществляются посредством электромагнитного поля и распространяются с конечной скоростью, равной скорости света в данной среде.
Первое уравнение Максвелла
Первое уравнение Максвелла в интегральной форме – это обобщение закона электромагнитной индукции Фарадея:
Этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, выбранного в переменном магнитном поле. Таким образом, переменное магнитное поле создает в любой точке пространства вихревое индуцированное электрическое поле независимо от того, находится в этой точке проводник, или нет. Действительно, рассмотрим электромагнитную индукцию в контуре. Пусть контур, в котором индуцируется ток, неподвижен, а изменения магнитного потока обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменение магнитного поля вызывает появление в контуре сторонних сил, которые действуют на носители тока. Эти сторонние силы не могут быть тепловыми, химическими и т.п., они не могут также быть магнитными, так как магнитные силы не совершают работу. Таким образом, индукционный ток может быть обусловлен только возникающим в проводе электрическим полем. Обозначим напряженность этого поля
Известно, что Контур L и поверхность S неподвижны, поэтому операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:
Это выражение преобразуем по теореме Стокса:
тогда
- ротор поля Таким образом, изменяющееся во времени магнитное поле порождает электрическое поле. Это поле Итак, электрическое поле может быть как потенциальным, так и вихревым. В общем случае электрическое поле равно векторной сумме полей:
причем
Таким образом, существует взаимосвязь электрического и магнитного полей, поэтому раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электрическое поле создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем отсчета эти заряды движутся, и, следовательно, порождают не только электрическое, но и магнитное поле. Неподвижный провод с постоянным током создает в каждой точке пространства постоянное магнитное поле. Однако относительно других инерциальных систем этот провод находится в движении. Поэтому создаваемое им магнитное поле в любой точке с координатами (х,у,z) будет меняться, и , следовательно, порождать вихревое электрическое поле. Поле, которое относительно одной системы отсчета оказывается чисто магнитным, относительно других систем отсчета будет представлять совокупность электрического и магнитного полей, образующих единое электромагнитное поле.
Ток смещения. Второе уравнение Максвелла Если электромагнитное поле стационарно, то ротор вектора
Вектор
При этом дивергенция Рассмотрим теперь изменяющееся во времени поле. Пусть магнитное поле создается током, текущим при зарядке конденсатора от источника постоянного напряжение U (рис.1). Этот ток меняется во времени и при напряжении на конденсатора, равном U, прекращается. Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора. Проведем круговой контур Г, охватывающий провод, по которому течет ток к конденсатору ( рис. 1). Обозначим через
где Для поверхности
Рис. 1.
Таким образом, в случае изменяющихся во времени полей уравнение (3) несправедливо. Поэтому можно сказать, что в уравнении (3) не хватает одного слагаемого, которое зависит от производных полей по времени. Для стационарных полей это слагаемое равно нулю. Для согласования уравнений (3) и (4) Максвелл ввел слагаемое, которое имеет размерность плотности тока, и назвал его плотностью тока смещения. С учетом этого слагаемого для ротора вектора
Сумма плотности тока проводимости и плотности тока смещения называется плотностью полного тока:
Можно показать, что дивергенция тока смещения равна:
По теореме Гаусса
поменяем местами порядок дифференцирования по времени и координатам, получаем:
Подставим ( 6) в формулу (5):
Тогда для ротора вектора
Это второе уравнение Максвелла. Из него следует, что меняющееся во времени электрическое поле Термин «ток смещения» является чисто условным. Это изменяющееся во времени электрическое поле. Ток смещения обладает только одним физическим свойством – способностью создавать магнитное поле. Токи смещения не сопровождаются выделением ленц-джоулева тепла. Ток смещения есть везде, где есть меняющееся во времени электрическое поле. Внутри проводов, по которым течет переменный электрический ток, ток смещения также существует, но он пренебрежительно мал по сравнению с током проводимости. Учет токов смещения приводит к тому, что цепи непостоянных токов становятся замкнутыми, токи смещения проходят в тех участках, где нет проводников, например, между обкладками плоского конденсатора. Известно, что
В этом выражении Ток смещения сквозь произвольную поверхность S, очевидно, равен потоку вектора плотности тока смещения через эту поверхность:
В интегральной форме второе уравнение Максвелла имеет вид:
- циркуляция вектора напряженности магнитного поля по произвольному замкнутому вектору L равна алгебраической сумме макротоков и токов смещения сквозь поверхность, натянутую на этот контур. Таким образом, электрическое и магнитное поля неразрывно связаны и могут взаимно порождать друг друга. Они образуют единое электромагнитное поле.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
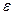 , относительной магнитной проницаемости
, относительной магнитной проницаемости  и удельной электрической проводимости
и удельной электрической проводимости 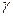 .
. . (1)
. (1) . Электродвижущая сила равна циркуляции вектора
. Электродвижущая сила равна циркуляции вектора 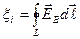 .
. (здесь используется частная производная т. к.
(здесь используется частная производная т. к.  является функцией не только времени, но и координат) . Магнитный поток
является функцией не только времени, но и координат) . Магнитный поток  , поэтому
, поэтому  .
. .
. ,
, (2)
(2) , создаваемого неподвижными зарядами. Электростатическое поле потенциально, его линии напряженности начинаются и заканчиваются на зарядах, ротор вектора
, создаваемого неподвижными зарядами. Электростатическое поле потенциально, его линии напряженности начинаются и заканчиваются на зарядах, ротор вектора  ,
, .
. в каждой точке поля равен плотности тока проводимости:
в каждой точке поля равен плотности тока проводимости: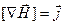 . ( 3)
. ( 3) связан с плотностью заряда в той же точке уравнением непрерывности:
связан с плотностью заряда в той же точке уравнением непрерывности: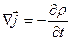 . (4)
. (4) поверхность, пересекающую провод и ограниченную контуром Г. Тогда по Закону полного тока
поверхность, пересекающую провод и ограниченную контуром Г. Тогда по Закону полного тока ,
, - сила тока, заряжающего конденсатор.
- сила тока, заряжающего конденсатор.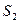 , не пересекающей провод с током ( рис. 1), имеем:
, не пересекающей провод с током ( рис. 1), имеем: .
. Этот результат является заведомо неверным, т .к. и поверхность
Этот результат является заведомо неверным, т .к. и поверхность  ( рис. ). Циркуляция вектора
( рис. ). Циркуляция вектора  .
. .
. . (5)
. (5)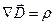 , продифференцировав это выражение по времени, имеем:
, продифференцировав это выражение по времени, имеем: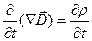 ,
, . (6)
. (6) , и
, и 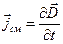 .
.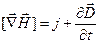 . (7)
. (7) порождает магнитное поле
порождает магнитное поле  , где
, где  – вектор поляризации. Тогда плотность тока смещения в диэлектрике
– вектор поляризации. Тогда плотность тока смещения в диэлектрике .
. определяет плотность тока смещения в вакууме,
определяет плотность тока смещения в вакууме,  называется плотностью тока поляризации. Он представляет собой плотность тока, обусловленного упорядоченным перемещением связанных зарядов в диэлектрике при изменении его поляризации. Это смещение зарядов в молекулах неполярного диэлектрика или поворот молекул – диполей в полярных диэлектриках.
называется плотностью тока поляризации. Он представляет собой плотность тока, обусловленного упорядоченным перемещением связанных зарядов в диэлектрике при изменении его поляризации. Это смещение зарядов в молекулах неполярного диэлектрика или поворот молекул – диполей в полярных диэлектриках. .
. ,
,