
|
|
Тема 4. Граничные задачи, уравнения и методыК классификации электромагнитных явлений Уравнения (2.1), (2.2) в Теме 2 позволяют классифицировать электромагнитные процессы и получить ряд соотношений, используемых в следующих главах для иллюстрации и тестирования численных методов на простейших примерах. 4.1.1. Уравнения электростатики.Самыми простыми являются неизменные во времени поля при отсутствии токов, т.е.
Используя тождество
и, подставив во второе уравнение (4.1), получаем в случае однородной среды для скалярного потенциала уравнение Пуассона
Общий вид решения этого уравнения Пуассона для неограниченной области имеет вид
где
При наличииграниц раздела сред (рис.4.1) выполняются следующие граничные условия:
где индексами 1 и 2 отмечены значения векторов поля в первой и второй средах соответственно;
Рис. 4.1. Граничные условия.
Граничные условия (4.6) с учётом (1.26) для потенциалов в первой
Если вторая среда является идеальным проводником, то вектора поля во второй среде равны нулю. Граничные условия для электростатического потенциала на поверхности S проводника имеют вид
где нормаль
или как задача Неймана, в которой вместо граничных условий для потенциалов Для линейных сред в силу линейности уравнений электростатики вводится понятие ёмкости C [Фарада] системы проводников. В частном случае двух проводников с зарядом q и потенциалами
Энергия электростатического поля определяется общим соотношением [12]
или в более удобной форме для локального распределения зарядов
Задания Задание 4.1 Найти и нарисовать распределение скалярного потенциала электростатического поля между двумя концентрическими цилиндрами (в предположении бесконечно протяженной структуры). Граничные условия: а. a = 0.01 м, b = 0.04 м, V0 = 6 В. б. a = 0.02 м, b = 0.04 м, V0 = 6 В. в. a = 0.02 м, b = 0.08 м, V0 = 6 В. г. a = 0.01 м, b = 0.04 м, V0 = 9 В. д. a = 0.02 м, b = 0.04 м, V0 = 9 В. е. a = 0.02 м, b = 0.08 м, V0 = 9 В. ж. a = 0.01 м, b = 0.04 м, V0 = 12 В. з. a = 0.02 м, b = 0.04 м, V0 = 12 В. и. a = 0.02 м, b = 0.08 м, V0 = 12 В.
Решение (стр.197, пример 4.7) Краевая задача формулируется как задача Дирихле (4.9). В силу симметрии решаем уравнение Лапласа в цилиндрической системе координат
Показать, что В силу симметрии
Решая последовательно это уравнение имеем:
где константы определяются из граничных условий
Откуда
Используя MATLAB строим распределение скалярного потенциала электростатического поля между двумя концентрическими цилиндрами, полагая, что
clear; clf
a = 0.01; b = 0.04; V0 = 6;
radius = a: 0.001: b; voltage = V0 * log(radius / b) ./ log(a / b); plot (radius, voltage)
xlabel ('\rho') ylabel ('V') grid on
Задание 4.2 Двухмерное распределение потенциала аппроксимируется выражением а. б. в. г. д. е. ж. Решение (стр.190, пример 4.4) Так как Используя MATLAB строим распределение скалярного потенциала электростатического поля u и электрического заряда clear; clf
xmin = -5; xmax = 5; ymin = -5; ymax = 5; step = 0.2;
[x, y] = meshgrid(xmin: step: xmax, xmin: step: xmax); voltage = (x .^ 2 + y .^ 2) / 4; surf(x, y, voltage)
hold on charge = del2(voltage); mesh (x, y, charge) view(-37.5, 20) xlabel ('x', 'fontsize', 12) ylabel ('y', 'fontsize', 12) zlabel ('\rho_v, V(x, y)', 'fontsize', 12)
Задание 4.3 Двухмерное распределение потенциала в районе
а. б. в. г. д. е. ж. з Решение (стр.224, пример 4.16) Уравнение Пуассона имеет вид clear; clf;
V0 = 1; eps = 1;
xmin = -2; xmax = 2; ymin = -2; ymax = 2; step = 0.1;
eps_0 = 8.854187817e-12; eps_a = eps * eps_0;
[x, y] = meshgrid (xmin: step : xmax, ymin: step: ymax); z = V0 * exp(-x .^ 2 - y .^ 2);
% Умножаем на 4, т.к. del2 делит оператор Лапласа на 2 * N, где N - % размерность матрицы ro = -del2(z, step) * 4 * eps_a;
subplot (2, 1, 1) surf(x, y, z) view(-45, 10) xlabel('x') ylabel('y') zlabel('u')
subplot (2, 1, 2) mesh(x, y, ro) view(-45, 10) xlabel('x') ylabel('y') zlabel('\rho_s')
% Аналитическая проверка ro_anal = 4 * V0 * exp (-x .^ 2 - y .^ 2) .* (1 - x .^ 2 - y .^ 2) * eps_a;
% Расчет разности между аналитикой и тем, что рассчитывалось с помощью del2 delta = abs (ro - ro_anal); delta_max = max (max(delta))
Метод конечных разностей Метод конечных разностей (МКР) [5] базируется на решении дифференциальных уравнений в частных производных, представленных в конечно-разностной форме. Метод достаточно универсальный, требует минимальной аналитической подготовки, и легко программируем, однако требует обращения матричных уравнений большого порядка. МКР создаёт промежуточную базу для метода конечных элементов и метода конечных разностей во временной области. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а уравнения, для электрического поля, называемого электростатическим, принимают вид
, а уравнения, для электрического поля, называемого электростатическим, принимают вид
 . (4.1)
. (4.1) , вводят понятие скалярного потенциала электростатического поля
, вводят понятие скалярного потенциала электростатического поля , (4.2)
, (4.2) . (4.3)
. (4.3)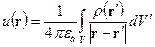 , (4.4)
, (4.4) – радиус-вектор точек наблюдения и интегрирования соответственно. Для тех областей, где заряд отсутствует (
– радиус-вектор точек наблюдения и интегрирования соответственно. Для тех областей, где заряд отсутствует (  ) (4.3) переходит в уравнение Лапласа
) (4.3) переходит в уравнение Лапласа . (4.5)
. (4.5) (4.6)
(4.6)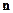 – единичный вектор нормали к поверхности, направленный в первую среду;
– единичный вектор нормали к поверхности, направленный в первую среду;  – поверхностная плотность электрических зарядов.
– поверхностная плотность электрических зарядов.
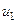 второй сред
второй сред  принимают вид
принимают вид . (4.7)
. (4.7)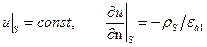 , (4.8)
, (4.8) распределение
распределение  на каждом из них неизвестно и краевые задачи формулируются как задача Дирихле
на каждом из них неизвестно и краевые задачи формулируются как задача Дирихле (4.9)
(4.9)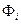 задаются граничные условия типа (4.8).
задаются граничные условия типа (4.8). и
и 
 . (4.10)
. (4.10) , (4.11)
, (4.11) . (4.12)
. (4.12)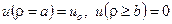 .
.
 . (1)
. (1) , где
, где  .
. и
и  . В результате (1) принимает вид:
. В результате (1) принимает вид: . (2)
. (2) , (3)
, (3) (4)
(4) . Соответственно из (3) потенциал электростатического поля между двумя концентрическими цилиндрами равен
. Соответственно из (3) потенциал электростатического поля между двумя концентрическими цилиндрами равен .
.
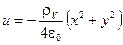 . Показать, что эта функция удовлетворяет уравнению Пуассона и построить поверхности распределения потенциала и электрического заряда
. Показать, что эта функция удовлетворяет уравнению Пуассона и построить поверхности распределения потенциала и электрического заряда  , Кл/м3. Поверхности строятся в интералах
, Кл/м3. Поверхности строятся в интералах  ,
,  с шагом 0.2 м.
с шагом 0.2 м.






 , то заданное распределение потенциала удовлетворяет двухмерному уравнению Пуассона
, то заданное распределение потенциала удовлетворяет двухмерному уравнению Пуассона  .
.
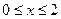 и
и  описывается выражением
описывается выражением  . Продифференцировать аналитически, а также, используя MATLAB, реализовать численное дифференцирование уравнения Пуассона при
. Продифференцировать аналитически, а также, используя MATLAB, реализовать численное дифференцирование уравнения Пуассона при  , и построить графики плотности электрических зарядов
, и построить графики плотности электрических зарядов  , Кл/м2 , а также распределение потенциала. Графики строятся с шагом 0.1 по осям.
, Кл/м2 , а также распределение потенциала. Графики строятся с шагом 0.1 по осям.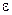 =1, V0 = 1 В.
=1, V0 = 1 В. . Использовать в MATLAB функцию del2.
. Использовать в MATLAB функцию del2.